大连海事大学2019计算机考研,大连海事大学计算机考研——选择部分
题型判断(20*1)+ 选择(10*2)+简答(含树和森林的转化,时间复杂度,二叉排序树,平衡二叉树,KMP,Hash表,程序输出)+证明(15*1) + 编程(15*1)
选择
Head Tail运算从一个表中,用Head(H),Tail(T)分离出一个元素原则:H操作提取第一个元素(原子或广义表);T操作去掉第一个元素(原子或广义表);写顺序是从后往前写例1,L=((( (a,b), e , ( (x), d) ))) 从中提取x初始:((( (a,b), e , ( (x), d) )))第一步,HH(去两个括号):( (a,b), e , ( (x), d) )第二步,T(去掉首元素): ( e , ( (x), d) )第三步,T (去掉首元素): ( ( (x), d) )第四步,H (提取首元素): ( (x), d)第五步,H (提取首元素): (x)第六步,H (提取首元素): x综上,从表中提取X的步骤为:HHHTTHH
2. 二维数组
二维数组,列(行)序为主序顺序存储,告诉一个点的地址,
每个元素占几个存储单元,求另一个点的地址。
分析:这种的画图做就可以,仔细些,难度不大。
3. 单链表存储队列
不带头的单链表存储队列,队头指向队头结点,队尾指向队尾结点,
在进行插入操作时:只需修改队尾指针
分析:链表是顺序存储,插入只能在队尾插入,因此只需要移动队尾指针
4.循环队列
循环队列是【0..m】,则数组的长度是m+1;
因为是队列,所以进队从后面进,移动rear指针;出队从前面出,移动front指针
5.折半查找
有序,顺序表,折半查找, 27个元素, 查找失败时,至少需要与关键字比较的次数:27
分析:折半查找查找失败至少需要与关键字的比较次数:log2(x)向下取整
6.m阶B树
1.非终端结点至多有m个指针,m-1个关键字
至少有(m/2向上取整)个指针,(m/2向上取整)-1 个关键字
2.根结点,至少两个指针(分支),1个关键字
3.所有叶子节点都在同一层上,且不带任何信息。
7.四维数组
例:四维数组B【1..3,2..8,0..5,1..8】以行主序 顺序存储,每个元素占2个存储单元,B【1,4,0,1】地址2000,则B【2,3,4,5】地址?
分析:四维数组B【1..3,2..8,0..5,1..8】(3,7,6,8)(3-1+1,8-2+1,5-0+1,8-1+1)
2000+【(2-1)*7*6*8 + (3-4)*6*8 + (4-0)*8 + (5-1)】*2 = 2648
8.排序
1.冒泡排序:逆序的情况下,比较次数最多
2.比较次数
最好的情况:直接插入排序: O(n)
冒泡:O(n) //最好,直接插,冒的好,即原数列有序
简单选择排序:O(n) //与原始序列无关(折半插入同样无关)
快速:O(n)
希尔: O(n)
归并: O【(log2(n)】
3.时间复杂度
平均情况:快速,希尔,归并,堆 (快些归队): O【nlog2(n)】
其他: O(n)
最坏情况:快速O(n),其他与平均相同
最好情况:简单插入排序:O(n)
4.空间复杂度
快速: O【log2(n)】
归并: O(n),
基数: O(rd),
其余: O(1)
5.辅助空间
堆排序 O(1)
直接选择排序O(1)
归并排序O(1)
快速排序O(log2n)
直接插入排序O(1)
5.每一趟都可以选出一个元素放到其最终位置上的是:
交换类(冒泡,快速)、选择类(简单选择,堆)
6.{50,80,30,40,70,60},快速排序,以第一个为基准,一趟后的结果:
9. 查找
对长度为n的顺序表进行顺序查找时,查找失败需要与键值的比较次数:n+1
折半查找,查找失败至少需要的比较次数:log2(n)向下取整
10. 图
例1.G是有8个顶点的非连通简单无向图,该图最多有( 21 )条边
分析:全连通图 边 M 和 点N的关系满足:M = N(N-1) /2
反过来看,即问有()条边,最少有8个点
M = (16-21) , N ≥ 7 ;( 7对应的最大是21,最小是6对应的+1,15+1 = 16)
即当M有(16 -21)条边,连通图最少有 7个顶点, 非连通图最少有8个顶点
所以,M最大为21
例2.G是一个非连通无向图,共有(22-28)条边,该图至少有( 9 )个顶点。
分析:全连通图 边 M 和 点N的关系满足:M = N(N-1) /2
当M = (22-28), N(N-1) /2 ≥(22-28),解得:8≤N<9,即N = 8
因为非连通,所以连通的加1,即8+1 = 9
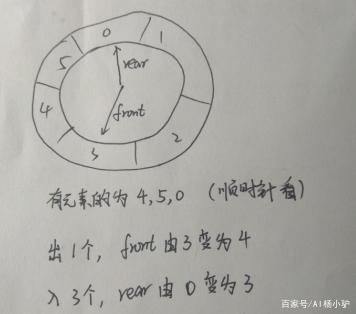
11. 循环队列
大小为6的数组实现循环队列,front = 3 ,rear = 0;删除一个,进队三个,
front = ? rear = ? (4 , 3)
分析:队列,先进先出。删除在队头front,进入在队尾rear。
12. 图
邻接矩阵 - 稠密图
邻接多重表- 无向图
十字链表 - 有向图
邻接表 - 稀疏图
补充:
1. 一个堆又是一个完全二叉树
2.n个节点的huffman树,有(n+1)/2个叶子节点。
3.在一颗深度为3的树中,有2个度为3的节点,1个度为2的节点,度为0的节点为?
分析:此题中没有度为1的节点,总分支数 = 总节点数 - 1;
即 n0 + n2(1 )+ n3(2) = (2*3 + 1*2) -1
解得:n0 = 6;
4. 65个节点的完全二叉树,(根的层次号为1)的深度为:7
分析:1+2+4+8+16+32 = 63 6层最多63个节点,7层最(64-127)
结语:判断选择的先更新这些,肯定还有漏掉的,以后必定补充上。
明天开始更新答题的,必然每日一更,直到结束!!!
举报/反馈