一维离散动力学系统的混沌研究【基于matlab的动力学模型学习笔记_8】

摘 要：混沌（Chaos）是指发生在确定系统中的貌似随机的不规则运动，本文将基于几种经典的一维动力学方程系统，根据其动力学方程研究其混沌产生过程以及相对应的MATLAB仿真。

/*仅当作学习笔记，若有纰漏欢迎友好交流指正，此外若能提供一点帮助将会十分荣幸*/

目录

0 引言

1 正弦函数型动力学微分方程的混沌

1.1系统的混沌

1.2系统分岔值的求解

2 Logistic映射

2.1系统的混沌

3 余弦函数型动力学微分方程的混沌

3.1系统的混沌

4 总结

参考文献

---

0 引言

混沌（Chaos）是指发生在确定系统中的貌似随机的不规则运动，长期以来，人们在认识和描述运动时，大多只局限于线性动力学描述方法，即确定的运动有一个完美确定的解析解。但是自然界在相当多情况下，非线性现象却起着很大的作用。混沌指确定性系统产生的一种对初始条件具有敏感依赖性的回复性非周期运动。混沌理论隶属于非线性科学，只有非线性系统才能产生浑沌运动。1963年美国气象学家Lorenz在分析天气预报模型时，首先发现空气动力学中混沌现象，该现象只能用非线性动力学来解。于是，1975年混沌作为一个新的科学名词首先出现在科学文献中。从此，非线性动力学迅速发展，并成为有丰富内容的研究领域。该学科涉及非常广泛的科学范围从电子学到物理学，从气象学到生态学，从数学到经济学等。

一般地，如果一个接近实际而没有内在随机性的模型仍然具有貌似随机的行为，就可以称这个真实物理系统是混沌的。一个随时间确定性变化或具有微弱随机性的变化系统，称为动力系统，它的状态可由一个或几个变量数值确定。而一些动力系统中，两个几乎完全一致的状态经过充分长时间后会变得毫无一致，恰如从长序列中随机选取的两个状态那样，这种系统被称为敏感地依赖于初始条件。而对初始条件的敏感的依赖性也可作为混沌的一个定义。

本文将从经典的一维混沌系统入手，以此为基础研究动力学系统的发展、混沌的产生以及相应的MATLAB仿真，借此对混沌建立一个完整的认识与理解。

1 正弦函数型动力学微分方程的混沌

1.1系统的混沌

该动力学微分方程的状态变量随时间的变化是离散的，也可以称之为离散动力学微分系统，其方程表达式为：

其中：

使用MATLAB计算随着的逐渐增大，迭代的值，程序如下：

f=@(a,x)a*sin(pi*x);%动力微分方程(补充：@(x)表示匿名函数，可以接受输入并返回输出)
hold on;
for x0=-1:0.1:1% x的取值迭代
    for a=0:0.01:1%系统函数的取值
        y=diedai(f,a,x0);
        for count=1:32
            plot(a,y(count),'k.');
            hold on;
        end
    end
end
子函数：
function y=diedai(f,a,x1)
N=32;
y=zeros(N,1);
for i=1:1e4
    x2=f(a,x1);
    x1=x2;
    y(mod(i,N)+1)=x2;
end
end

这里为了表达清晰明了，分为主函数和子函数两部分，其中子函数主要负责迭代部分。

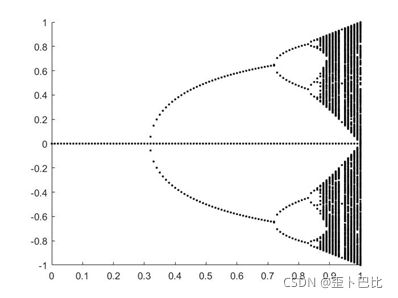
仿真结果：

其中，横轴代表系统参数，纵轴为迭代值x.从图中可以看出，在0.3附近出现第一次分岔、在0.7左右出现第二次分岔、0.8左右出现第三次分岔、而到了0.86附近，图像出现混沌状况。

1.2系统分岔值的求解

在这里，当迭代x出现不止一个值并且最大值与最小值之间的差大于0.001时，我们认为系统出现分岔。

①求解第一个分岔值(在0.3左右)

MATLAB程序：

f=@(a,x)a*sin(pi*x);
format short;
x0=0.1;
 for a=0.3:0.0001:0.32%为了节省计算量，将第一个分岔值预估在0.3-0.32之间
    y=diedai(f,a,x0);
    if max(y)>0.001
        disp(a);
        break;
    end
 end
计算结果：
 
求得第一个分岔值为0.3183.
②求解第二个分岔值(在0.7左右)
MATLAB程序：
f=@(a,x)a*sin(pi*x);
format short;
x0=0.1;
 for a=0.7:0.0001:0.72%为了节省计算量，将第一个分岔值预估在0.7-0.72之间
    y=diedai(f,a,x0);
    if max(y)- min(y)>0.001
        disp(a);
        break;
    end
 end
计算结果：
 
求得第二个分岔值为0.7200.
③求解第三个分岔值(在0.8左右)
f=@(a,x)a*sin(pi*x);
format short;
x0=0.1;
 for a=0.8:0.0001:0.85%为了节省计算量，将第一个分岔值预估在0.8-0.85之间
    y=diedai(f,a,x0);
    if abs(y(32)-y(30))>0.001%从图像可以看出，由于迭代值已经分岔到关于横轴对称，因此用最大值与最小值之间的差值来衡量分岔已经不合理了，因此利用diedai,m函数里面的第32次迭代(最后依次迭代)和第30次迭代之间的差值来比较。
        disp(a);
        break;
    end
 end

计算结果：

求得第三个分岔值为0.8333.

2 Logistic映射

2.1系统的混沌

同第一章中的三角函数混沌模型一样，Logistic映射也是一维离散动力学系统，其定义为：

 

其中为系统参数，

其程序为：

clc, clear,  
hold on
for a=0:0.01:4
    x1=0.1;%初值设置
    for i=1:100
        x2=a*x1*(1-x1);%动力学迭代方程
        x1=x2;
        if i>70, plot(a,x1,'.'), end
    end
end
xlabel('\alpha'), ylabel('\it x','rotation',0)

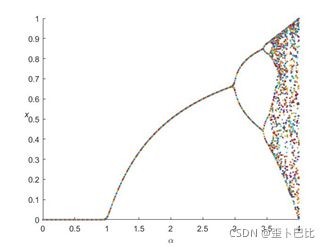
仿真结果：

Logistic映射也称为虫口模型，因为这个模型最初就是用来描述昆虫的数量随时间的变化。由于食物、生存空间、天敌等原因，昆虫不可能无限制的增加，当到达一个数量级后，昆虫之间就会出现竞争，“适者生存”然后适应能力更强的才能够生存。这也类似于当系统参数足够大时，系统图像所出现的混沌状况。

与正弦型函数引起的混沌状况不同，虫口模型混沌在系统参数大于之后昆虫数才开始有变化。换句话说就是当系统参数大于1的情况下，该系统才能完成数量上的迭代增加，即种群才能够接续发展。但当系统参数达到3.5左右时，即进入混沌状态，该种群也不能很好的发展生存。

因此，对于该模型下的种群，当系统参数时，种群能够得到较好的发展，也可以把理解为Logistic映射的适宜增长参数。

3 余弦函数型动力学微分方程的混沌

3.1系统的混沌

该动力学微分方程的状态变量随时间的变化是离散的，也可以称之为离散动力学微分系统，其方程表达式为：

 

 其中：系统的参数

程序段：

f=@(a,x)a*cos(pi*x);%动力微分方程(补充：@(x)表示匿名函数，可以接受输入并返回输出)
hold on;
for x0=-1:0.1:1% x的取值迭代
    for a=0:0.01:1%系统函数的取值
        y=diedai(f,a,x0);
        for count=1:32
            plot(a,y(count),'k.');
            hold on;
        end
    end
end
子函数：
function y=diedai(f,a,x1)
N=32;
y=zeros(N,1);
for i=1:1e4
    x2=f(a,x1);
    x1=x2;
    y(mod(i,N)+1)=x2;
end
end

同第一章中的正弦函数的混沌程序类似，这里为了表达清晰明了，也分为主函数和子函数两部分，其中子函数主要负责迭代部分，主函数负责键入方程。

仿真结果：

其中，横轴代表系统参数，纵轴为迭代值.从仿真图可以看出，在0.4附近出现第一次分岔、在0.6左右出现第二次分岔、0.65左右出现第三次分岔、而后，系统进入混沌状况。 

4 总结

根据上述三个例子，我们可以看出对于一维系统而言，其系统参数对于相应动力学方程以及系统的发展起着决定性作用。当虫口模型的系统参数小于1时，系统甚至无法完成正常的迭代繁衍，而当系统参数大于3.5时，系统又将进入混沌态。可以看出对于系统参数的调节控制，极大的影响着生物模型的发展。

而对于正弦和余弦函数对应的混沌，即使初始值设立相同，但系统的发展变化却是千差万别，这也可以很容易的看出动力学方程对于系统发展乃至混沌产生的巨大影响。

参考文献

1. 李静,向菲,张军朋.一种基于混沌的数字图像信息加密方案.电子设计工程,2019,27(12):84-88.
2. 彭川,莫海芳.基于Logistic混沌序列的鲁棒数字水印方案.计算机仿真,2012,29(9):278-282.
3. 柯赟,蒋天发.基于离散余弦和Contourlet混合变换域的图像水印方案.武汉大学学报：工学版,2012,45(2):264-267.