【自动驾驶控制算法】 第二讲 三个坐标系与运动学方程
声明:【自动驾驶控制算法】系列是博主对B站up主:忠厚老实的老王所分享教学内容的学习笔记,并且该系列每篇博客都会将博主听课后总结的纸质版笔记附于文末,供大家参考。
B站up主:忠厚老实的老王是一位研究汽车领域,无人驾驶方向及其相关方向的大佬,也算是博主在无人驾驶方向的启蒙老师。所以研究相关领域的朋友推荐去听一听他的视频讲解。
文章目录
- 前言
- 1. 三个坐标系
- 2. 运动学方程
- 注:博主笔记
前言
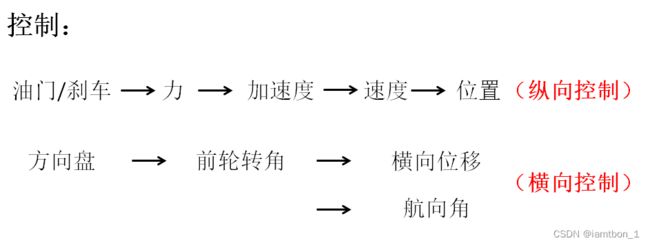
自动驾驶控制算法:PID算法,LQR算法,MPC算法
PID、LQR算法:百度Apollo使用这两种算法
MPC算法:学术界一般使用MPC算法,其控制效果优于PID和LQR算法,但是计算量太大,只存在于仿真。
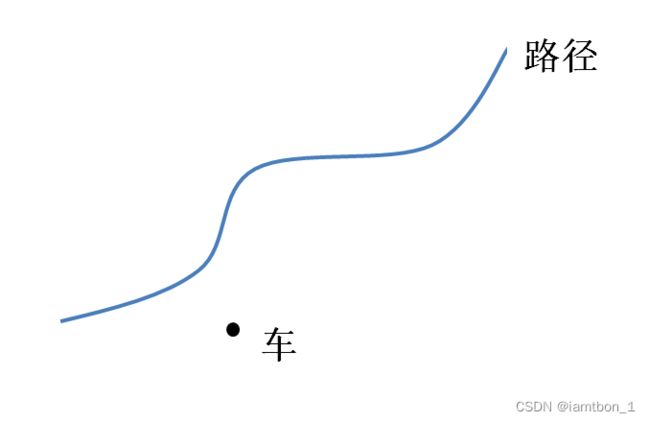
控制的前提是路径规划,教程中默认已有路径规划。
1. 三个坐标系
本教程一律采用右手系。
右手系:当右手的拇指指向 x x x轴时,食指指向 y y y轴,中指指向 z z z轴。
左手系:当左手的拇指指向 x x x轴时,食指指向 y y y轴,中指指向 z z z轴。
一般数学,物理学等都是右手系。
而一般计算机学科,图形,视觉方向是左手系。
自动驾驶又是一个跨学科较大的行业,所以在参考学习自动驾驶的相关文献资料时,一般要先了解作者的学科背景。
三个坐标系:
2. 运动学方程
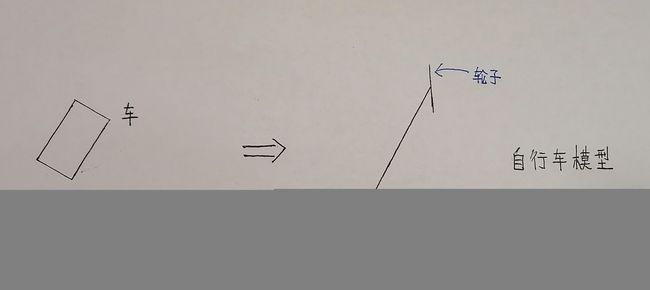
(1)、简化汽车模型:
(2)、建立微分方程:
几何关系——运动学模型(不考虑轮胎变形)
牛顿力学——动力学模型(考虑轮胎变形)
所以运动学模型只适应于轮胎变形小的情况。如速度比较低,转弯半径比较大,规划的轨迹比较平缓。对于行驶状况比较激烈的情况,误差较大。
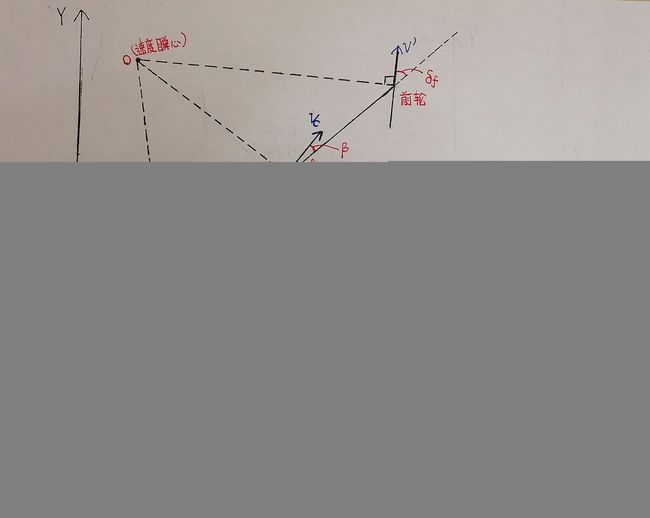
质心的速度 v c v_{c} vc :可用速度瞬心法来求(理论力学知识点)
(3)、运动学模型:
X ˙ = v ∗ cos ( β + α ) \dot{X} =v*\cos (\beta +\alpha ) X˙=v∗cos(β+α) Y ˙ = v ∗ sin ( β + α ) \dot{Y} =v*\sin (\beta +\alpha ) Y˙=v∗sin(β+α) φ ˙ = v R \dot{\varphi } =\frac{v}{R} φ˙=Rv
只体现了质心速度 v v v对 X ˙ \dot{X} X˙、 Y ˙ \dot{Y} Y˙、 φ ˙ \dot{\varphi } φ˙的影响,没体现前轮转角 δ f \delta _{f} δf对 X ˙ \dot{X} X˙、 Y ˙ \dot{Y} Y˙、 φ ˙ \dot{\varphi } φ˙的影响。
因此进一步推导:
设质心到前轮的距离为 a a a,到后轮的距离为 b b b
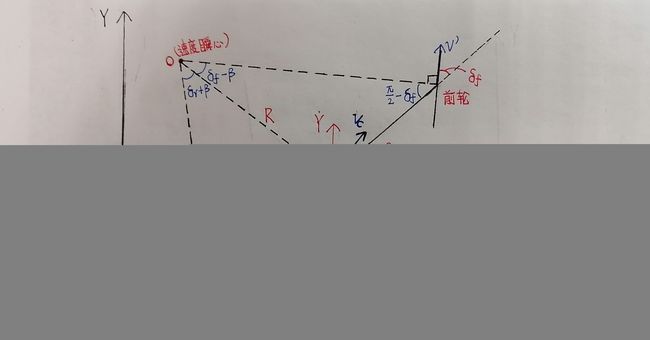
使用正弦定理: a sin ( δ f − β ) = R sin ( π 2 − δ f ) \frac{a}{\sin (\delta _{f} -\beta )} =\frac{R}{\sin (\frac{\pi }{2}-\delta _{f} )} sin(δf−β)a=sin(2π−δf)R b sin ( δ r + β ) = R sin ( π 2 − δ r ) \frac{b}{\sin (\delta _{r} +\beta )} =\frac{R}{\sin (\frac{\pi }{2}-\delta _{r} )} sin(δr+β)b=sin(2π−δr)R化简得: a R = sin ( δ f − β ) sin ( π 2 − δ f ) = sin δ f ∗ cos β − sin β ∗ cos δ f cos δ f = tan δ f ∗ cos β − sin β \frac{a}{R} =\frac{\sin (\delta _{f} -\beta )}{\sin (\frac{\pi }{2}-\delta _{f} )} =\frac{\sin \delta _{f} *\cos \beta -\sin \beta *\cos \delta _{f} }{\cos \delta _{f} }=\tan \delta _{f} *\cos \beta -\sin \beta Ra=sin(2π−δf)sin(δf−β)=cosδfsinδf∗cosβ−sinβ∗cosδf=tanδf∗cosβ−sinβ b R = sin ( δ r + β ) sin ( π 2 − δ r ) = sin δ r ∗ cos β + sin β ∗ cos δ r cos δ r = tan δ r ∗ cos β + sin β \frac{b}{R} =\frac{\sin (\delta _{r} +\beta )}{\sin (\frac{\pi }{2}-\delta _{r} )} =\frac{\sin \delta _{r} *\cos \beta +\sin \beta *\cos \delta _{r} }{\cos \delta _{r} }=\tan \delta _{r} *\cos \beta +\sin \beta Rb=sin(2π−δr)sin(δr+β)=cosδrsinδr∗cosβ+sinβ∗cosδr=tanδr∗cosβ+sinβ
但是质心是会变化的(车上载重不同,质心自然不同)
因此进一步推导:
L = a + b L=a+b L=a+b为轴距,轴距是不会因质心变化而变化的。
a + b R = ( tan δ f + tan δ r ) ∗ cos β = tan δ f + tan δ r \frac{a+b}{R} =(\tan \delta _{f} +\tan \delta _{r} )*\cos \beta =\tan \delta _{f} +\tan \delta _{r} Ra+b=(tanδf+tanδr)∗cosβ=tanδf+tanδr ⇓ \Downarrow ⇓ 1 R = tan δ f + tan δ r L \frac{1}{R} =\frac{\tan \delta _{f} +\tan \delta _{r} }{L} R1=Ltanδf+tanδr
得出 R R R与 δ f \delta _{f} δf、 δ r \delta _{r} δr的关系。
得到运动学方程:
X ˙ = v ∗ cos ( β + φ ) \dot{X} =v*\cos (\beta +\varphi ) X˙=v∗cos(β+φ) Y ˙ = v ∗ sin ( β + φ ) \dot{Y} =v*\sin (\beta +\varphi ) Y˙=v∗sin(β+φ) φ ˙ = v R = v ∗ ( tan δ f + tan δ r ) L \dot{\varphi } =\frac{v}{R}=\frac{v*(\tan \delta _{f} +\tan \delta _{r}) }{L} φ˙=Rv=Lv∗(tanδf+tanδr)
使用运动学方程的前提条件:
在低速条件下,认为车不会发生侧向滑动(漂移),即 v y ≈ 0 v_{y} \approx 0 vy≈0
所以: β = arctan v y v x = 0 \beta =\arctan \frac{v_{y}}{v_{x}} =0 β=arctanvxvy=0一般汽车后轮不转向,在低速条件下认为: δ r ≈ 0 \delta _{r} \approx 0 δr≈0
所以最终的运动学方程:
X ˙ = v ∗ cos φ \dot{X} =v*\cos \varphi X˙=v∗cosφ Y ˙ = v ∗ sin φ \dot{Y} =v*\sin \varphi Y˙=v∗sinφ φ ˙ = v ∗ tan δ f L \dot{\varphi } =\frac{v*\tan \delta _{f} }{L} φ˙=Lv∗tanδf
其中 φ \varphi φ是横摆角,质心速度 v = v x v=v_{x} v=vx
因为 β = 0 \beta =0 β=0,所以横摆角 ≈ \approx ≈航向角。