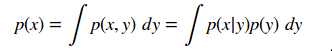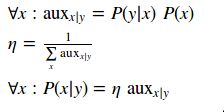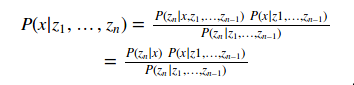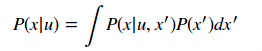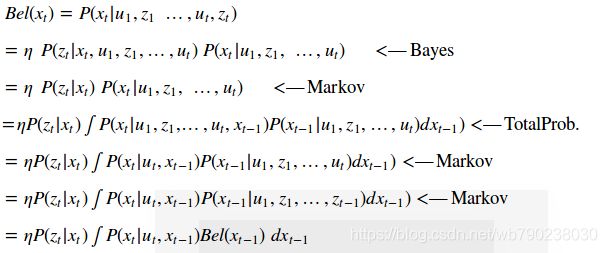【算法基础学习 1】贝叶斯滤波

 

(一). 概率基础回顾

我们先来回顾一下概率论里的基本知识：

1. X:  表示一个随机变量，如果它有有限个可能的取值{x1,x2,⋯,xn}

2. p(X=xi):表示变量X的值为 xi的概率。

3. p(⋅):称为概率质量函数(probability mass function).

    例如：一个家里有3个房间，机器人在各个房间的概率为 p(room)={0.1,0.3,0.6}.

4. 如果X在连续空间取值，p(x)称为概率密度函数(probability density function)，

p(x∈(a,b))=

 

                                                                                     图1. 概率密度函数曲线示例

5. 联合概率：p(X=x  and  Y=y)=p(x,y)，称为联合概率密度分布。如果X和Y是相互独立的随机变量，p(x,y)=p(x)p(y)。

6. 条件概率：p(X=x|Y=y)是在已知Y=y的条件下，计算X=x的概率。

                                                                                            p(x|y)=p(x,y)/p(y)

                                                                                      p(x,y)=p(x|y)p(y)=p(y|x)p(x)

 

    如果x和y相互独立，则：

                                                                                                  p(x|y)=p(x)

7. 全概率公式：

  离散情况下:

  连续情况下：

(二). 贝叶斯公式

2.1 贝叶斯公式

基于条件概率公式和全概率公式，我们可以导出贝叶斯公式：

• 这里面x一般是某种状态；y一般是代表某种观测。
• 我们称P(y|x)为causal knowledge，意即由x的已知情况，就可以推算y发生的概率，例如在图2的例子中，已知如果门开着，则z=0.5m的概率为0.6；如果门关着，则z=0.5m的概率为0.3。
• 我们称P(x)为prior knowledge，是对x的概率的先验知识。例如在图2的例子中，可设门开或关的概率各占50%
• P(x|y)是基于观测对状态的诊断或推断。贝叶斯公式的本质就是利用causal knowledge和prior knowledge来进行状态推断或推理。

例1:：

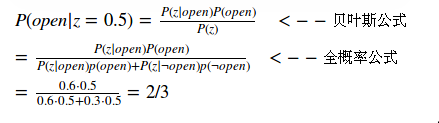
在图2所示的例子中，机器人根据观测的到门的距离，估算门开或关的概率，若测量到门的距离为z=0.5m，则可用条件概率描述门开着的概率:

                                                                                                   P(open|z=0.6)=?

 

                                                                            图 2.机器人根据观测计算门开或关的概率

 

2.2 贝叶斯公式的计算

可以看到贝叶斯公式的分母项P(y)，同P(x|y)无关，所以可以把它作为归一化系数看待：

 

所以基于causal knowledge和prior knowledge进行条件概率计算的过程如下：

Algorithm:

2.3 贝叶斯公式中融合多种观测

在很多应用问题中，我们会用多种观测信息对一个状态进行猜测和推理，贝叶斯公式中是如何融合多种观测的呢？

我们简单推导一下：

所以有：

2.4 贝叶斯递推公式

由此，我们来推导贝叶斯滤波的递推公式：

P(x|z1,…,zn)=?

我们把zn看做y，把z1,…,zn−1看做z，代入上面的公式：

再由Markov属性，在x已知的情况下，zn同{z1,…,zn–1}无关，所以：

从而我们得到贝叶斯的递推公式：

 

例2：在例1的基础上，如果机器人第二次测量到门的距离仍然为0.5米， 计算门开着的概率。

所以，第二次z=0.5m的观测增大了对门开着的概率的置信程度。

(三). 如何融入动作？

在实际问题中，对象总是处在一个动态变化的环境中，例如：

1. 机器人自身的动作影响了环境状态
2. 其它对象，比如人的动作影响了环境状态
3. 或者就是简单的环境状态随着时间发生了变化。

如何在Bayes模型中来描述动作的影响呢?

1. 首先，动作所带来的影响也总是具有不确定性的
2. 其次，相比于观测，动作一般会使得对象的状态更为模糊（或更不确定）。

我们用u来描述动作，在x′状态下，执行了动作u之后，对象状态改变为x的概率表述为：

                                                                                                             P(x|u,x′)

动作对状态的影响一般由状态转移模型来描述。如图3所示，表示了“关门”这个动作对状态影响的转移模型。这个状态转移模型表示：关门这个动作有0.1的失败概率，所以当门是open状态时，执行“关门”动作，门有0.9的概率转为closed状态，有0.1的概率保持在open状态。门是closed的状态下，执行“关门”动作，门仍然是关着的。

                                                                          图3. “关门”动作的状态转移模型

执行某一动作后，计算动作后的状态概率，需要考虑动作之前的各种状态情况，把所有情况用全概率公式计算：

• 连续情况下：

• 离散情况下：

例3：在例2的基础上，如果按照图3所示的状态转移关系，机器人执行了一次关门动作， 计算动作后门开着的概率？

所以，执行一次关门动作后，门开着的概率变为了0.08.

(四). 贝叶斯滤波算法

4.1 算法设定

由上述推导和示例，我们可以给出贝叶斯滤波的算法，算法的输入输出设定如下。

• 1.系统输入

1. 1到t时刻的状态观测和动作：dt={u1,z1…,ut,zt}
2. 观测模型：P(z|x)
3. 动作的状态转移模型：P(x|u,x′)
4. 系统状态的先验概率分布P(x)

• 2.期望输出
  1. 计算状态的后延概率，称为状态的置信概率：

4.2 算法基本假设

贝叶斯滤波的基本假设：

        1. Markov性假设: t时刻的状态由t−1时刻的状态和t时刻的动作决定。t时刻的观测仅同t时刻的状态相关，如图4所示：

                                                                                          图4. Markov模型

 

     2. 静态环境，即对象周边的环境假设是不变的

       3. 观测噪声、模型噪声等是相互独立的

4.3 Bayes滤波算法

基于上述设定和假设，我们给出贝叶斯滤波算法的推导过程：

其中第一步采用贝叶斯公式展开，第二步使用Markov性质(zt仅由xt决定)；第三步使用全概率公式对xt−1进行展开；第四步继续使用Markov性质(xt仅由xt−1和ut决定)；第五步继续使用Markov性质，因为xt−1同ut无关，最终得到Bel(xt)的递推公式。

可见递推公式中分为两个步骤，部分是基于xt−1,ut预测xt的状态；ηP(zt|xt)部分是基于观测zt更新状态xt.

4.3 Bayes滤波算法流程

所以，Bayes滤波的算法流程图如图5所示。如果d是观测，则进行一次状态更新，如果d是动作，则进行一次状态预测。

                                                                           图5. Bayes滤波的算法流程

我们看到，在进行状态预测时，需要对所有可能的x′状态进行遍历，使得基本的Bayes模型在计算上成本是较高的。

4.3 Bayes滤波算法的应用

Bayes滤波方法是很多实用算法的基础，例如：

• Kalman滤波
• 扩展Kalman滤波
• 信息滤波
• 粒子滤波

等，我们在下一节介绍Kalman滤波。

参考：

http://www.cnblogs.com/ycwang16/p/5995702.html

https://blog.csdn.net/sonictl/article/details/8787106