贝叶斯滤波

1.概率基础

概率论中，假设随机变量为$X$。
当$X$离散时，即$X$存在有限个取值$\{x_1,x_2,\dots ,x_n\}$，概率可表示为：
$$P(X=x_i)=p$$表示$X$的值为$x_i$的概率，
$$p(x)=\{\begin{array}{ll}P(X=x),& x\in \{x_1,x_2,\dots ,x_n\}\\ 0,& x\notin \{x_1,x_2,\dots ,x_n\}\end{array}$$$p(x)$称为概率质量函数(probability mass function)；

当$X$连续时，概率可表示为：
$$P(a<X<b)={\int }_a^{b}p(x)\mathrm{d}x$$表示$X$的取值在$(a,b)$区间内的概率，
$p(x)$称为概率密度函数(probability density function)。

联合概率
多个随机变量分别满足各自条件的概率，
离散时，$p(x,y)=P(X=x,Y=y)$，
连续时，$P(a<X<b,c<Y<d)={\int }_c^d{\int }_a^{b}p(x,y)\mathrm{d}x\mathrm{d}y$，$p(x,y)$为联合概率密度函数。

条件概率
$$p(x|y)=P(X=x|Y=y)$$表示在$Y=y$的条件下，$X=x$的概率。
$$\begin{gathered} p(x|y)=\frac{p(x,y)}{p(y)} \\ p(x,y)=p(x|y)p(y)=p(y|x)p(x) \end{gathered}$$

全概率公式
离散时，$$p(x)=\sum _{y}p(x,y)=\sum _{y}p(x|y)p(y)$$
连续时，$$p(x)=\int p(x,y)\mathrm{d}y=\int p(x|y)p(y)\mathrm{d}y$$
$p(x)$是$X$的边缘分布。

贝叶斯公式
$$p(x|y)=\frac{p(x,y)}{p(y)}=\frac{p(y|x)p(x)}{p(y)}$$在贝叶斯定理中，每个名词都有约定俗成的名称：
$p(x|y)$被称作后验概率(Posterior probability)；
$p(x)$和$p(y)$被称作先验概率(Prior probability) 或边缘概率；
$p(y|x)$是条件概率，也称为似然性/可能性(likelihood)

2.贝叶斯滤波

滤波是一种方法、手段，在时移（time-varying）系统中，通过对带有噪声的前k个观测$y_{1:k}$来估计隐状态$x_k$的处理方法，记作$x_k|y_{1:k}$；

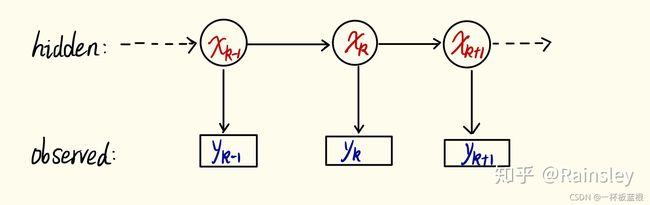
这就是随机动态系统中的滤波问题，我们需要根据带有误差的实际测量数据对目标的位置、速度、加速度等进行估计。在二战期间，它是由于军事方面的需要而产生的，在通讯、控制等领域获得了广泛的应用。根据上述特性，具体地在全球定位系统(GPS)、多目标追踪、导航等方面的应用很多。

贝叶斯滤波模型假设
我们考虑的是随机动态系统，自然要用概率来刻画，所以我们需要一个概率状态空间模型，要素如下：
$x_k$k时刻的状态
$y_k$k时刻的观测
$p(x_k|x_{k-1})$状态转移概率
$p(y_k|x_k)$观测概率

贝叶斯滤波方程及其推导
初始化：
初始状态的先验分布为$p(x_0)$
预测步：
利用前k-1个观测来估计第k个隐状态$x_k$，可以根据全概率公式：
$$p(x_k|y_{1:k-1})=\int p(x_k|x_{k-1})p(x_{k-1}|y_{1:k-1})\mathrm{d}{x}_{k-1}$$
更新步：
利用预测和新加入的第k个观测$y_k$，结合贝叶斯公式：
$$p(x_k|y_{1:k})=\frac{1}{Z_k}p(y_k|x_k)p(x_k|y_{1:k-1})$$
其中$$Z_k=\int p(y_k|x_k)p(x_k|y_{1:k-1})\mathrm{d}{x}_k$$

这样的话，我们就确定了贝叶斯滤波框架，在这个框架下，我们就可以导出下面一系列的滤波：卡尔曼滤波、三种非线性滤波等等。