Machine learning week 9(Andrew Ng)

Recommender systems

1.Collaborative filtering

1.1 Making recommendations

Introduction

1.2 Using per-item features

Cost function：

1.3 Collaborative Filtering algorithm

Predict x feature via the known parameters $w$ and $b$

The cost function is similar to before.

# Y (4778, 443) R (4778, 443)
# X (443, 10)
# W (443, 10)
# b (1, 443)
# num_features 10
# num_movies 4778
# num_users 443
def cofi_cost_func(X, W, b, Y, R, lambda_):
    """
    Returns the cost for the content-based filtering
    Args:
      X (ndarray (num_movies,num_features)): matrix of item features
      W (ndarray (num_users,num_features)) : matrix of user parameters
      b (ndarray (1, num_users)            : vector of user parameters
      Y (ndarray (num_movies,num_users)    : matrix of user ratings of movies
      R (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th user
      lambda_ (float): regularization parameter
    Returns:
      J (float) : Cost
    """
    nm, nu = Y.shape
    J = 0
    ### START CODE HERE ###  
    for j in range(nu):
        w = W[j,:]
        b_j = b[0,j]
        for i in range(nm):
            x = X[i,:]
            J += R[i,j] * ((np.dot(w,x) + b_j - Y[i,j])**2)
    J /= 2 
    J += (lambda_ / 2) * (np.sum(np.square(W)) + np.sum(np.square(X)))
    ### END CODE HERE ### 

    return J


def cofi_cost_func_v(X, W, b, Y, R, lambda_):
    """
    Returns the cost for the content-based filtering
    Vectorized for speed. Uses tensorflow operations to be compatible with custom training loop.
    Args:
      X (ndarray (num_movies,num_features)): matrix of item features
      W (ndarray (num_users,num_features)) : matrix of user parameters
      b (ndarray (1, num_users)            : vector of user parameters
      Y (ndarray (num_movies,num_users)    : matrix of user ratings of movies
      R (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th user
      lambda_ (float): regularization parameter
    Returns:
      J (float) : Cost
    """
    j = (tf.linalg.matmul(X, tf.transpose(W)) + b - Y)*R
    J = 0.5 * tf.reduce_sum(j**2) + (lambda_/2) * (tf.reduce_sum(X**2) + tf.reduce_sum(W**2))
    return J

1.4.Binary labels: favs, likes and clicks

Judge whether the customer likes it（Binary labels）

1.5.Mean normalization

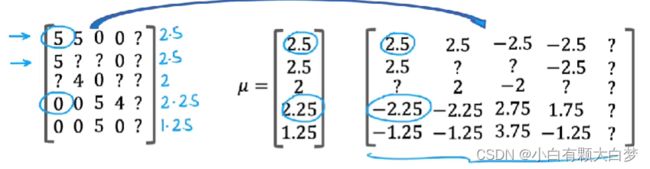
And in fact, the effect of this algorithm is it will cause the initial guesses for the new user Eve to be just equal to the mean of whatever other users have rated these five movies. And that seems more reasonable to take the average rating of the movies rather than to guess that all the ratings by Eve will be zero.

1.6.TensorFlow

1.7.Finding related items

2. Content-based filtering

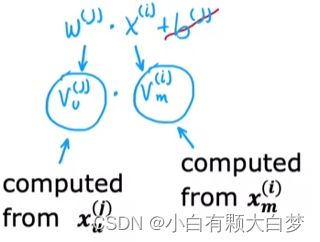
2.1. Collaborative filtering vs Content-based filtering

Our purpose is to predict the value, so we should transform the features of users and movies to vector $v_u,v_m$, which have the same dimension.

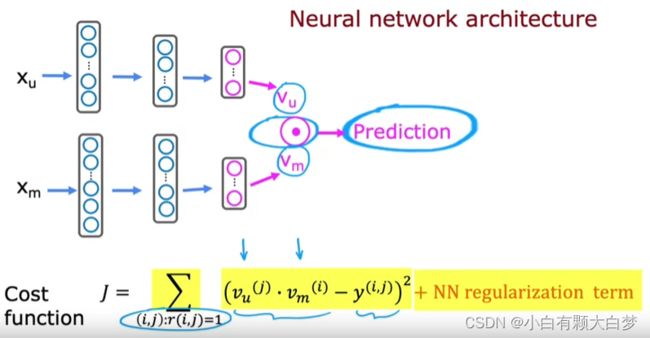
2.2. Deep learning for content-based filtering

Both of them have 32 numbers although $x_u$ and $x_m$ are different.

And $||v_m^{(k)}-v_m^{(i)}|{|}_{min}^2$ is the most similar movie to movie $i$.

2.3. Recommending from a large catalog

When the catalog is too large, thousands of millions of times every time a user shows up on your website becomes computationally infeasible. So, we should prepare before.
Having precomputed the most similar movies to every movie, we can just pull up the results using a look-up table. And then we can retrieval and rank

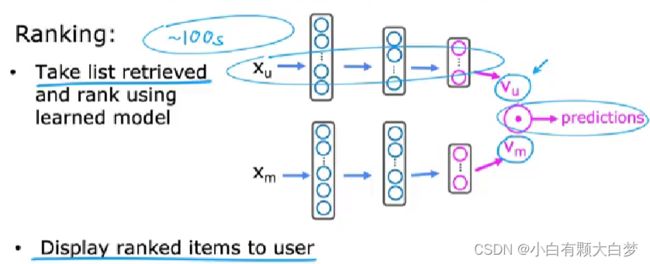
Rank them by the prediction value from high to low.