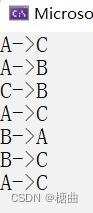【数据结构】深度讲解栈、栈的应用举例、栈和递归的实现教你全面认识栈
目录
- 一.栈
-
- 1.栈的概念及结构
- 2.栈的实现
-
- stack.h
- Stack.c
- 二.栈的应用举例
-
- 1.数制转换
- 2.有效的括号
- 3.迷宫求解
- 三.栈与递归的实现
-
- 1.栈和递归
- 2.迷宫问题递归实现
- 3.汉诺塔栈实现
一.栈
1.栈的概念及结构
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。**进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。**栈中的数据元素遵守后进先出LIFO(last in first out)的原则。
进栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫出栈。出数据也在栈顶。
2.栈的实现
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小,而且栈对数组头部的操作只有在栈中数据个数为1或0时,才对数组头部进行操作,数组完全符合栈的条件,相对于链表优势更大,实现更简单。
通常我们将top指针指向栈顶的下一个位置,表示该位置为下一个数据入栈存储的位置。当top = 0时表示空栈。
另一方面,栈在使用的过程中所需要最大空间的大小很难估计,因此,一般来说,在初始化设空栈时不设置栈的最大容量,而是根据实际需求动态增加空间。
stack.h
头文件,包含栈所有的函数声明、结构体声明
#pragma once
#includeStack.c
包含所有函数的定义
1.初始化栈
//初始化栈
void StackInit(Stack* ps)
{
assert(ps);
//初始化两种方式
//方式1
ps->top = 0;
ps->capcity = 0;
ps->st = NULL;
//方式2
// 使用该方法,下面的入栈函数需要修改
//ps->st = (STDataType*)malloc(sizeof(STDataType) * 4);
//if (!ps->st)
//{
// perror("malloc fail");
// exit(-1);
//}
//ps->capcity = 4;
//ps->top = 0;
}
方法1:直接将栈的容量赋值为0,对存放数据的数组赋为NULL,入栈操作时,在进行赋值
方法2:在初始化时,向内存申请空间并赋给存放数据的指针,将申请空间的大小就是栈的容量。
这两种方法都可以使用。
2.入栈
//入栈
void StackPush(Stack* ps, STDataType x)
{
assert(ps);
if (ps->capcity == ps->top)
{
int size = (ps->top == 0) ? 4 : ps->top * 2;
STDataType* tmp = (STDataType*)realloc(ps->st, sizeof(STDataType) * size);
if (!tmp)
{
perror("realloc fail!");
exit(-1);
}
ps->capcity = size;
ps->st = tmp;
}
ps->st[ps->top] = x;
ps->top++;
}
首先,判断栈剩余的的空间是否足够,若是不够,进行扩容操作,向内存申请更多的空间,并修改栈的容量。
其次,将首元素存入栈顶,在将栈顶加1,
因为初始时,栈顶的位置为0,存放1个元素时,栈顶的位置为1,存放第二个元素时,栈顶的位置为2,每增加一个元素,栈顶移动一位。
3.出栈
//出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);//判断栈中是否还有数据
ps->top--;
}
出栈操作十分简单,先使用断言栈中是否还有数据,若是有进行出战操作,否则提示出错(无法对空的栈进行出栈操作)。
最后,将栈顶减1即可,因为每次入栈和从栈中取数据都是依据栈顶来实现的,直接将对栈顶进行操作,当下次入栈时就会覆盖掉之前的数据,从栈中取数据也是取减1后栈顶的数据,这样写是合适的。
4.获取栈顶元素
//获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->st[ps->top-1];
}
同时,判断栈中是否还有数据。
因为栈顶是要比存入栈的最后一个数据的下标高一位,返回下标为栈顶-1的数据即可
5.获取栈中有效元素个数
//获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
assert(ps->top >= 0);
return ps->top;
}
返回栈顶的即可,栈顶是多少,栈中就有多少个数据。
6.检测栈是否为空
//检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->top == 0;
}
如果栈顶为0,表示栈为空,返回1,否则为假,返回0
7.销毁栈
//销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->st);
ps->st = NULL;
ps->capcity = 0;
ps->top = 0;
}
栈中存储数据的空间是向内存申请的需要释放,否则会造成内存泄漏。
Stack.c代码
#define _CRT_SECURE_NO_WARNINGS 1
#include "Stack.h"
//初始化栈
void StackInit(Stack* ps)
{
assert(ps);
//初始化两种方式
//方式1
ps->top = 0;
ps->capcity = 0;
ps->st = NULL;
//方式2
// 使用该方法,下面的入栈函数需要修改
//ps->st = (STDataType*)malloc(sizeof(STDataType) * 4);
//if (!ps->st)
//{
// perror("malloc fail");
// exit(-1);
//}
//ps->capcity = 4;
//ps->top = 0;
}
//入栈
void StackPush(Stack* ps, STDataType x)
{
assert(ps);
if (ps->capcity == ps->top)
{
int size = (ps->top == 0) ? 4 : ps->top * 2;
STDataType* tmp = (STDataType*)realloc(ps->st, sizeof(STDataType) * size);
if (!tmp)
{
perror("realloc fail!");
exit(-1);
}
ps->capcity = size;
ps->st = tmp;
}
ps->st[ps->top] = x;
ps->top++;
}
//出栈
void StackPop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
//获取栈顶元素
STDataType StackTop(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->st[ps->top-1];
}
//获取栈中有效元素个数
int StackSize(Stack* ps)
{
assert(ps);
assert(ps->top >= 0);
return ps->top;
}
//检测栈是否为空,如果为空返回非零结果,如果不为空返回0
int StackEmpty(Stack* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->top == 0;
}
//销毁栈
void StackDestroy(Stack* ps)
{
assert(ps);
free(ps->st);
ps->st = NULL;
ps->capcity = 0;
ps->top = 0;
}
二.栈的应用举例
由于栈结构具有后进先出的固有特性,使得栈成为程序设计中的有用工具。接下来我们将讨论几个栈应用中典型的例子。
1.数制转换
十进制数N和其他d进制数的转换是计算机实现计算的基本问题,其解决方法很多,其中一个简单算法基于下列原理:

例如:(1348)10 = (2504)8 其运算过程如下:

这道题使用栈来实现是非常简单的,将N和8求余的结果放入栈中,最终依次出栈即为最终结果。也许,有人就会有疑问:用数组直接实现不也很简单?对的,用数组直接实现也不难,但栈的引用简化了程序设计的问题,使思考范围缩小。使用数组真正要去想的不是解出这道题的思路,而是去考虑数组下标增减等细节问题。
//对于输入的任意一个非零的十进制整数,打印出与它等值的八进制数
void conversion()
{
Stack s;
StackInit(&s);//创建空栈
int N = 0;
printf("十进制:");
scanf("%d", &N);
while (N)
{
StackPush(&s, N % 8);
N = N / 8;
}
printf("八进制:");
while (!StackEmpty(&s))
{
printf("%d", StackTop(&s));
StackPop(&s);
}
}
2.有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = “()”
输出:true
示例 2:
输入:s = “()[]{}”
输出:true
示例 3:
输入:s = “(]”
输出:false
(这是Leetcode上的一道题,大家可以直接点击标题进入网站答题。)
解题思想:
我们将“ [ { ( ”这三种开括号放入栈中,如果出现另外三种闭括号,将该闭括号与栈顶的元素做对比,这样简单的入栈出栈操作即可确定括号是否匹配。

bool isValid(char* s) {
Stack st;
StackInit(&st);
while (*s)
{
if (*s == '[' || *s == '{' || *s == '(')
{
StackPush(&st, *s);//将出现的开括号全都放入栈中
s++;
}
else//当出现闭括号,将其与栈顶数据做对比
{
if (StackEmpty(&st))//如果此时栈为空,匹配失败
return false;
char tmp = StackTop(&st);
StackPop(&st);
if (*s == ']' && tmp == '[')
{
s++;
continue;
}
else if (*s == '}' && tmp == '{')
{
s++;
continue;
}
else if (*s == ')' && tmp == '(')
{
s++;
continue;
}
return false;
}
}
if (!StackEmpty(&st))//如果此时栈不为空,表示括号不匹配
return false;
return true;
}
3.迷宫求解
求迷宫中从入口到出口的所有路径使一个经典的程序设计问题。由于计算机解迷宫时,通常用的是“穷举求解”的方法,即从入口出发,顺某一方向向前探索,若能走通,则继续往前走;否则沿原路退回,换一个方向继续探索,甚至所有可能的通路都探索到为止。为了保证在任何位置上都沿原路退回,显然需要一个后进先出的结构保存从入口到当前位置的路径。因此,在求迷宫通路的算法中应用“栈”也就是自然而然的事。

思想
- 白方块:通道
- 阴影线方块:墙
假设当前位置为“在搜索过程中某一时刻所在图中某个方块位置”,则求迷宫中一条路径的算法基本思想为:
当前路径可通,入栈,继续探索下一个位置,若当前路径不可通,则出栈,出栈后判断此时栈顶位置其他的下一个位置;若该通道块四周的4个方块均不可通,则继续出栈,如此重复直到到达出口。
“当前位置”的四个方块为相邻的上、下、左、右上相邻的方块。
注意:所谓的可通指的是未曾走到过的通道块,即要求该方块位置不仅是通道块,而且即不在当前路径上,也不是曾经纳入过的路径的通道块,否则只能进入死循环。
typedef struct location
{
int x; //当前位置的横坐标
int y; //当前位置的纵坐标
int next; //指向的下一个位置
}local;//栈的元素类型
int n = 8;
char Maze[8][8] =
{ {'O','X','X','X','X','X','X','X'},
{'O','O','O','O','O','X','X','X'},
{'X','O','X','X','O','O','O','X'},
{'X','O','X','X','O','X','X','O'},
{'X','O','X','X','X','X','X','X'},
{'X','O','X','X','O','O','O','X'},
{'X','O','O','O','O','X','O','O'},
{'X','X','X','X','X','X','X','O'}
};
int H[4] = { -1,0,1,0 };
int V[4] = { 0,1,0,-1 };
void MazePrint()
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%c ", Maze[i][j]);
}
printf("\n");
}
}
void DFS(Stack* st)
{
StackInit(st);
local start = { 0,0,0 };
StackPush(st, start);
Maze[start.x][start.y] = ' '; //将入栈的位置变为空字符方便区分
while (!StackEmpty(st))
{
int top = StackSize(st) - 1; //取栈顶元素的下标
while (st->st[top].next < 4)//每个当前位置共用四个方位可以选择,每个方向遍历一遍
{
if (st->st[top].x == n - 1 && st->st[top].y == n - 1)//判断是否到达出口
{
MazePrint();
return;
}
if (Maze[st->st[top].x + H[st->st[top].next]][st->st[top].y + V[st->st[top].next]] == 'O')//判断该位置是否入栈
{
Maze[st->st[top].x + H[st->st[top].next]][st->st[top].y + V[st->st[top].next]] = ' ';//将入栈位置变为空字符
local cur = { st->st[top].x + H[st->st[top].next], st->st[top].y + V[st->st[top].next], 0 };//创建新的当前位置结点,方便入栈
st->st[top].next++;//修改当前位置的四个方向标记,表示此方向已经遍历,无论是否出栈,将不会在遍历
StackPush(st, cur);//入栈
top = StackSize(st) - 1;
continue;
}
st->st[top].next++;//修改当前位置的四个方向标记,表示此方向已经遍历,无论是否出栈,将不会在遍历
}
Maze[st->st[top].x][st->st[top].y] = 'O';//出栈前先将当前位置代表的字符回复,表示此路不通
StackPop(st);//出栈
}
}
三.栈与递归的实现
栈还有一个重要应用就是在程序设计语言中实现递归。一个直接调用自己或通过一系列的调用语句间接地调用自己的函数,称为递归函数。递归是算法中最常见的手段之一,它通常可以将一个复杂的大型的问题简化的简洁而清晰,很多递归算法常常要比非递归算法更容易设计,当问题本身涉及的数据结构是递归定义的时候,使用递归方法就更合适。
既然递归这么好,那我们为什么还要学着用栈去实现递归?
第一:在很多面试或笔试当中要求我们有这样的能力。比如快排的非递归写法就时常被拿来考察面试者。
第二:递归算法虽好,但它还是有很大的局限性,想要拥有一些东西,就必须要放弃一些。比如二叉树用递归遍历和非递归遍历就各有各的优势,我们可以用这两种方法达到不同的目的。
1.栈和递归
栈和递归的相互转换,采用相同的思想:
将第一个问题中的数据入栈或进入下一层递归,判断下一个问题的可执行性,继续保存当前数据继续入栈或进入下一次递归。
以此达到保存之前数据去解决新的问题的目的。
- 这里我们用之前讲的迷宫问题的递归实现和汉诺塔的栈实现来讲解栈和递归的联系。
2.迷宫问题递归实现
栈操作是将迷宫的下一个位置入栈,当无路可走时,做出栈操作,查找新的可以入栈的位置。
递归采用相同的思想:
代码
int n = 8;
char Maze[8][8] =
{ {'O','X','X','X','X','X','X','X'},
{'O','O','O','O','O','X','X','X'},
{'X','O','X','X','O','O','O','X'},
{'X','O','X','X','O','X','X','O'},
{'X','O','X','X','X','X','X','X'},
{'X','O','X','X','O','O','O','X'},
{'X','O','O','O','O','X','O','O'},
{'X','X','X','X','X','X','X','O'}
};
int H[4] = { -1,0,1,0 };
int V[4] = { 0,1,0,-1 };
void MazePrint()
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
printf("%c ", Maze[i][j]);
}
printf("\n");
}
}
void DFS(int x, int y)
{
if (x == n - 1 && y == n - 1)//判断是否道道出口
{
Maze[x][y] = ' ';
MazePrint();
return;
}
else
{
for (int i = 0; i < 4; i++)//将当前位置的周围四个位置依次遍历
{
if (x>0 && x<n && y>0 && y<n && Maze[x][y] == 'O')//判断当前位置是否是通道是否越界(我使用的VS2019不判断越界也可得到答案)
{
Maze[x][y] = ' ';//置为空字符,表示可行通道
DFS(x + H[i], y + V[i]);
Maze[x][y] = 'O';//该位置不可行,返回原值
}
}
}
}
int main()
{
int x = 0, y = 0;
DFS(x, y);
return 0;
}
- 从思想上看这和使用栈实现相同,但代码量明显减少。
- 在实际代码运行中,找到最终的出口就会输出,但是如上图的返回操作是递归到最后一层后依次退回之前递归的函数操作。
3.汉诺塔栈实现
汉诺塔我相信接触过递归的人都应该知道,如果对此了解不深的可以看这篇博客青蛙跳台阶和汉诺塔问题。
思路:
- 这里我们要使用栈去解决,栈的元素是什么?——结构体,汉诺塔需要定位三个位置和一个数量,如果一个个入栈在出栈,不方便
typedef struct node
{
int n; //传递盘数
char begin; //起始
char mid; //中转
char end; //放置位置
}Node;
- 循环的实现,和递归相同。
当传递盘数为1时,begin->end;
当传递盘数不为1时,进行分化:- 将n-1个盘子从begin移动到mid
- 将最后一个盘子从begin移动到end
- 将n-1个盘子从mid移动到end
因为是在栈上操作,每次进行循环时,都是对栈顶操作,如果按照123的顺序入栈,那就是在1还没有进行,n-1个盘子还没有移动到mid就继续操作,这明显是不对的。
所以我们按照321的顺序入栈,依次继续操作。
代码:
typedef struct node
{
int n; //传递盘数
char begin; //起始
char mid; //中转
char end; //放置位置
}Node;
void hanoi(Stack* st)
{
while (!StackEmpty(st))
{
Node cur = StackTop(st);
StackPop(st);
if (cur.n == 1)
printf("%c->%c\n", cur.begin, cur.end);
else
{
Node tmp1 = { cur.n - 1,cur.mid,cur.begin,cur.end };
StackPush(st, tmp1);
Node tmp2 = { 1,cur.begin,cur.mid,cur.end };
StackPush(st, tmp2);
Node tmp3 = { cur.n - 1,cur.begin,cur.end,cur.mid };
StackPush(st, tmp3);
}
}
}
int main()
{
Stack st;
StackInit(&st);
Node nd = { 3,'A','B','C' };
StackPush(&st,nd);
hanoi(&st);
return 0;
}