基于模型预测控制MPC的光伏并网系统设计|太阳能发电|模型预测控制

        本课题提出一种基于最大功率点跟踪与有限集模型预测控制结合的光伏并网逆变策略，首先，针对模型预测控制算法在电网模型预测与控制时域中实时性不足等问题，引用快速求解MATMPC工具箱，降低MPC算法的单轮运算时间，显著提高系统的实时性与控制效果。再者，针对功率波动、电流震荡与延时等问题，利用改进的扰动跟踪法对最大功率点进行跟踪，采用2个采样周期预测值对计算和采样导致的延时进行补偿，有功功率能根据光照强度自适应调整，无功功率能迅速降到0左右，功率因数接近1，有效地提高了入网电流跟踪精度，降低了入网的电流畸变率。有限控制集模型预测控制(FCS-MPC)算法具有动态响应快、无超调、非线性和多目标控制等优点，因而在逆变器并网控制领域引起了广泛研究。但是FCS-MPC存在开关频率不固定和控制精度低的问题，使得并网滤波器的参数难以设计，同时在低调制比工况下，入网电能品质难以得到保证。本文主要研究解决FCS-MPC算法应用于三电平逆变器并网控制时开关频率不固定和控制精度低的问题。根据FCS-MPC算法的基本原理，首先建立了三电平逆变器交流侧入网电流的预测模型，并构建了多控制目标的目标函数。在此基础上，分析了计算和采样延时对电流跟踪控制的影响，并提出采用两步预测计算法对延迟进行补偿。同时结合参考电压矢量计算和扇区划分，对三电平逆变器的基本电压矢量进行离线预选，以实现降低在线寻优计算量的目的。本文设计了一套基于二极管中点钳位式三电平逆变器拓扑的并网的Simulink仿真平台，静态和动态并网实验结果表明，本文所提出的基于虚拟电压矢量输入控制集合的FCS-MPC具有动态响应快且无超调的优点，同时能够集中三电平逆变器桥臂的输出电压频谱，有效地提高入网电流跟踪精度，降低入网电流畸变率。仿真结果表明本文提出的方法能够取得更低的电流THD和更高的电流跟踪精度，切实有效地提高了入网电能品质。

背景及意义

光伏发电具有其具有显著的清洁性、安全性、广泛性、经济性，被认为是最优质的绿色能源之一，在长期的能源战略中具有重要地位；2021年3月，中央财经委员会第九次会议中指出“要构建清洁低碳安全高效的能源体系，控制化石能源总量，着力提高利用效能，深化电力体制改革，构建以新能源为主体的新型电力系统”我国是太阳能资源丰富的国家之一。在中国很多地区，每年的日照量都在2000小时以上，是太阳能资源大国。

存在问题

        光照强度变化、采样、计算等引起的功率波动、电流震荡与相位滞后问题与模型预测控制求解带约束的优化问题时计算代价较大，难以保证控制的实时性。

解决思路

        利用扰动观测法对光伏阵列的最大功率点进行跟踪，并网功率根据光照强度实现自适应调整，MPC中采用2个采样周期预测值对计算和采样导致的延时进行补偿，引入基于不精确灵敏度更新策略的快速计算MATMPC工具箱。

包含光伏阵列，逆变器及其负载，电网，锁相环，基于扰动观测法的MPPT，参考值计算，预测模型，目标函数，寻优算法。 

最大功率点跟踪原理

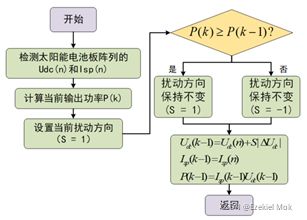
最大功率点追踪(MPPT)的目的就是对在任意时刻光伏阵列的工作电压值进行取样，通过一定的控制策略使其稳定工作在最大功率点Pm对应的工作电压Um处，在任意的环境变化中（如突然减少光强，温度剧烈上升等）都可以维持最大输出量，持续稳定的提供优质电能。扰动观察法（Perturbation and observation，P&O）的原理是当光伏阵列运行在某一工作电压下时，检测其输出功率，然后在这个工作电压基础上，添加一个比较小的扰动电压，以改变其输出功率的大小。若添加扰动电压之后，其输出功率增加，则说明添加的扰动电压方向是正确的，下一周期可以继续添加该方向的扰动电压;若添加扰动电压之后，其输出功率降低，则说明添加的扰动电压方向是不正确的，下一周期需要添加与该扰动电压方向相反的另一扰动电压。控制流程如图2-3所示。

模型预测控制设计

快速计算MATMPC工具箱：GitHub - chenyutao36/MATMPC

 SImulink仿真设计

 

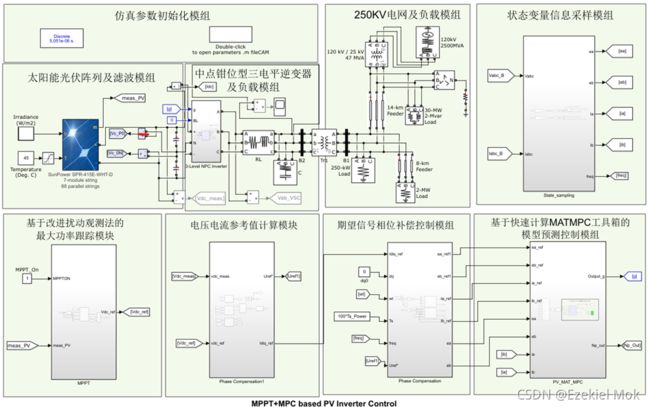
整体的仿真模型可以分为太阳能光伏阵列及滤波模组、250KV电网及负载模组、中点钳位型三电平逆变电路及负载模组、基于改进扰动观测法的最大功率点跟踪控制模块、期望信号相位补偿控制模组和基于快速计算MAT-MPC工具箱的模型预测控制模组。太阳能光伏阵列及滤波模组中太阳能电池板阵列选用的是SunPower SPR-415E-WHT-D，光伏阵列由86个平行串组成，每个串有7个串联的SunPower SPR-415E模块，光伏阵列块包含了五个参数模型，分别为电流源IL（光生电流）、二极管（I0和nI参数）、串联电阻Rs和并联电阻Rsh来表示模块的辐照度和温度相关I-V特性，该模块的阵列的I-V和P-V特性如图2-2所示，由图中可直接读出在45ºC的开路电压为575V、短路电流为550A，最大输出功率可达2.3KW。

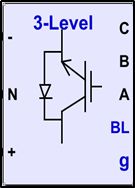
 根据图中三电平并网逆变器结构，该模块实现选定强制换向的中点钳位型三电平逆变电桥。串联RC缓冲电路与每个开关装置并联连接,在仿真中选取IGBT二极管作为功率电子器件，逆变器扼流圈RL和谐波滤波器C用于过滤IGBT电桥产生的谐波。Simulink模型如图所示。

 电网及负载电路包含了250 kVA 250V/25kV三相变压器将逆变器连接至公共配电系统。该电网被建模为典型的配电网。结构如图3-4所示。它包括两个25 kV反馈线、负载、接地变压器和一个等效的120 kV输电系统。接地变压模块用于在三相三线制系统中提供中性点，该变压器由三个之字形连接的双绕组变压器组成。

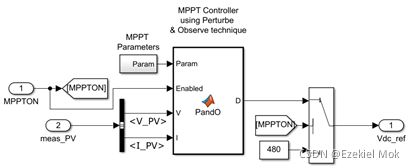
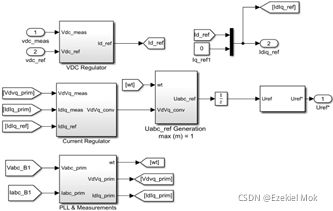
最大功率点跟踪（MPPT）控制器基于“扰动和观测”技术，该MPPT系统自动改变逆变器VDC调节器的VDC参考信号，以获得将从光伏阵列提取最大功率的直流电压。VDC调节器用于确定电流调节器所需的Id（有功电流）参考。在我们的示例中，Iq参考设置为零。PLL测量模块用于同步和电压/电流测量的需要。PWM发生器根据所需参考电压向IGBT生成触发信号。在我们的示例中，载波频率设置为1980 Hz，具体的Simulink模型如图所示

电压与电流参考值计算模块包含一个直流电压调节器，如图3-6所示，通过对参考直流电压与期望直流电压偏差的比例积分计算出直流分量作为参考电流Id和Iq（无功电流）,再经过锁相环获取期望信号相位，输入电流比例积分调节器与参考电压生成器产生模型预测控制器所需的期望控制电压信号。 

电压与电流参考值计算模块包含一个直流电压调节器，通过对参考直流电压与期望直流电压偏差的比例积分计算出直流分量作为参考电流Id和Iq（无功电流）,再经过锁相环获取期望信号相位，输入电流比例积分调节器与参考电压生成器产生模型预测控制器所需的期望控制电压信号。

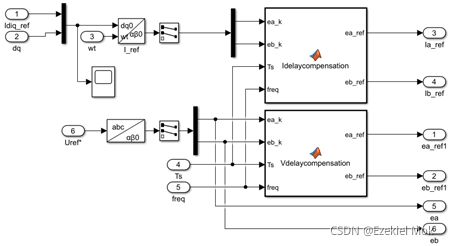
期望信号相位补偿模块包含一个电压补偿与电流补偿器，如图3-7所示，产生模型预测控制器所需要的期望信号的两步预测值。

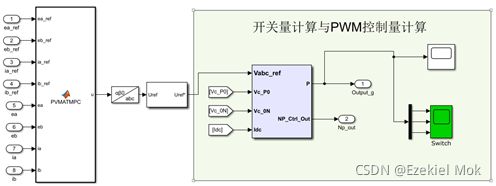
 基于快速计算MATMPC工具箱的模型预测控制模组模块了预测信息生成模块、模型预测控制模块开关量计算与PWM控制量计算模组，如图3-8所示，接收来自最大功率点跟踪模组生成的电流电压信号作为观测值。

 本模块采用两步预测消除延迟时间，然后通过矢量角补偿法在线计算所有受控变量在k+1时刻的预测值，选择代价最小的状态作为k时刻的最优状态并应用，可实现受控变量的误差最小，产生的控制量信号经过载波的调制产生PWM信号作用于逆变器电桥端。模型预测控制的算法流程包括光伏阵列经过光电转换将太阳能转换为电能，对输出的光伏直流电压与电流进行采样分析，将采样到的数据传递到MPC控制器与最大功率点跟踪控制器中作为实际输出值与参考值，最大功率点跟踪控制采用自适应补偿扰动观测法进行对输出功率点的实时动态跟踪，并将运算得到的参考三相电压输送到模型预测控制器中根据预设的代价函数滚动时域最优化输出PWM开关量到三电平逆变器，对逆变器电路中的开关电子管进行控制，实现最大功率跟踪，并把电流的THD降低到电网容许的范围之内。

仿真分析

设置总的仿真时长为0.5s，给定光伏阵列模型的初始输入辐照度为1000 W/m2，随后分别在0.2s与0.4s的时候降低到500 W/m2后返回到1000 W/m2，工作温度设定为45℃。如图所示，当达到稳态（约t=0.08秒）时，我们得到481 V的光伏电压（Vdc_mean），从光伏组件产生的功率（Pdc_mean）为236 KW,上述数值与光伏组件制造商的标准预期值是非常吻合的。 

太阳能电池阵列的输出功率和电压电流变化曲线如图所示，t=0.2秒时，太阳辐照度从1000 W/m^2迅速下降到500 W/m^2。由于MPPT运行，控制系统根据上述原理改变VDC参考电压，以便从光伏阵列中提取平均功率118 kW。可见太阳能电池的实际输出功率与太阳能电池阵列的理论最大功率接近，可见系统实现了最大功率跟踪。 

 

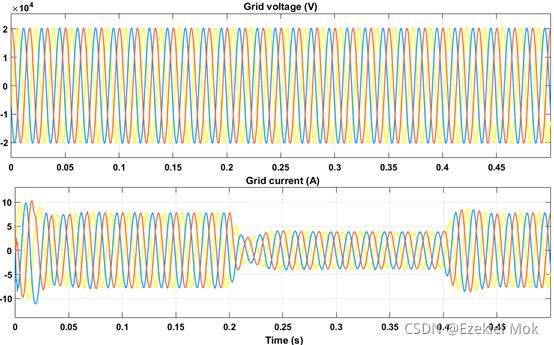
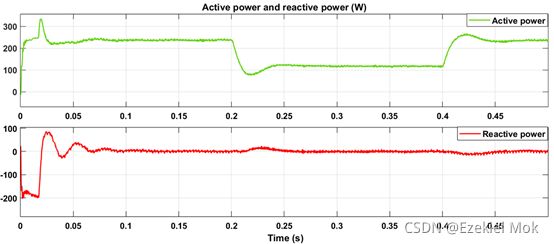
 图中表明并网电流与电网电压同频同相，即实现了单位功率因数并网。由图所示，由于光照度的变化，功率的振荡频率有所改善，系统的有功功率工作在最大功率点附近，无功功率恒定在0附近。可以得知由于扰动观察法和MPC算法的相结合共同控制开关量计算与PWM控制量计算模组T时，可以使得光伏阵列的输出功率尽可能的增大，减少功率的损失。

如图所示，当光伏输出功率由光照产生阶跃变化时，本文控制策略相较于传统的PI控制，并网电流能够更快速地响应到稳态正弦波。如图4-8所示，两步预测地并网电流总谐波畸变率为1.36%。可见两步基于有限状态集合模型预测控制方法与最大功率跟踪控制的有效性，在静态与动态条件下具有优越的响应性能。如图所示，最大功率跟踪过程中，实际电压能跟踪上参考轨迹。

function u = pvmpc(ea_ref,eb_ref,ia_ref, ib_ref, ea, eb, ia, ib)
import casadi.*
N = 2; % 离散区间数
Ts = 100*(5.051e-6); % 每个离散区间的长度
LR = [9.935088167568475e-05,3.745440000000000e-04];
% LR = [0.15;0.0015];
L=LR(1);
R=LR(2);
% 模型变量

I_a = SX.sym('I_a');
I_b = SX.sym('I_b');
I = [I_a; I_b];

u_a = SX.sym('u_a');
u_b = SX.sym('u_b');
u = [u_a; u_b];

I_a_ref = SX.sym('I_a_ref'); % 参数
I_b_ref = SX.sym('I_b_ref');
u_a_rel = SX.sym('u_a_rel'); % 参数
u_b_rel = SX.sym('u_b_rel'); % 参数
ref = [I_a_ref ;I_b_ref;u_a_rel ; u_b_rel];



I_0=[ia,ib]; %Vehicle 起始点位置向量



  xdot =(Ts/L)* [u(1)-ref(3); u(2)-ref(4) ];% +(1-(R*Ts/L))*[I(1);I(2)]; % 最后的动态模型

% 目标函数
 OBJ = 10*(I_a-ref(1))^2+(I_b-ref(2))^2;

% 构建动态方程
 f = Function('f', {I, u, ref}, {xdot, OBJ});
  


% 构建离散函数
X0 = MX.sym('X0', 2);
U = MX.sym('U',2);
P = MX.sym('P',4);
X = X0;
Q = 0;
[k,k_q]=f(X0,U,P);
X=(1-(R*Ts/L))*X +k;
Q=k_q;  
F = Function('F', {X0, U, P}, {X, Q}, {'x','u','p'}, {'xf', 'qf'});



%% 构建优化问题
w={};
w0 = [];
lbw = [];
ubw = [];
J = 0;
g={};
lbg = [];
ubg = [];

Para = MX.sym('Para',N,4);
% 初始条件
Xk = MX.sym('X0', 2);

w = [w, {Xk}];
lbw = [lbw; I_0'];
ubw = [ubw; I_0'];
w0 = [w0; I_0'];

% Formulate the NLP
for k=0:N-1
    
    % 输入变量
    Uk = MX.sym(['U_' num2str(k+1)], 2);
    w = [w, {Uk}];
     lbw = [lbw; -inf; -inf];
     ubw = [ubw; inf; inf];

    
    Fk = F('x', Xk, 'u', Uk, 'p', Para(k+1,:)');
    Xk_end = Fk.xf;
    J=J+Fk.qf;

    % 状态变量
    Xk = MX.sym(['X_' num2str(k+1)], 2);
    w = [w, {Xk}];
    lbw = [lbw; -inf; -inf];
    ubw = [ubw;  inf;  inf];

    g = [g, {Xk_end-Xk}]; 
    lbg = [lbg; 0; 0];
    ubg = [ubg; 0; 0];
end
% 预设轨迹作为参数
% 
% e_x_set = [ ea_ref(1), ea_ref(2)];
% e_y_set = [ eb_ref(1), eb_ref(2)];
e_x_set = [ ea, ea_ref(1)];
e_y_set = [ eb, eb_ref(1)];
x_set = [ia_ref(1), ia_ref(2)];
y_set = [ ib_ref(1), ib_ref(2)];
% x_set = [ia, ia_ref(1)];
% y_set = [ ib, ib_ref(1)];

p_set = [x_set; y_set;e_x_set; e_y_set]';
% 求解
prob = struct('f', J, 'x', vertcat(w{:}), 'g', vertcat(g{:}), 'p',Para);

opts.ipopt.print_level= 0;
opts.print_time = 0;
% solver = nlpsol('nlpsol', 'ipopt', prob, opts);


solver = nlpsol('solver', 'ipopt', prob, opts);
sol = solver('lbx', lbw, 'ubx', ubw,'lbg', lbg, 'ubg', ubg,'p',p_set);
s_opt = full(sol.x);

ia_opt = s_opt(1:4:end);
ib_opt = s_opt(2:4:end);
ua_opt = s_opt(3:4:end);
ub_opt = s_opt(4:4:end);

u = [ua_opt(1);ub_opt(1);0];
end