《机器学习》及实战三、决策树理论及实战

• Python版本： Python3.x
• 运行平台： Windows
• IDE： PyCharm
• 参考资料：《机器学习》（西瓜书）《机器学习实战》（王斌）
• 转载请标明出处：https://blog.csdn.net/tian121381/category_9748511.html
• 资料下载，提取码：9k59
  

一、前言

上节介绍的k-近邻算法可以很好地完成分类任务，但是它最⼤的缺点就是⽆法给出数据的内在含义，决策树的主要优势就在于数据形式非常容易理解。决策树的⼀个重要任务是为了数据中所蕴含的知识信息，因此决策树可以使⽤不熟悉的数据集合，并从中提取出⼀系列规则，在这些机器根据数据创建规则时，就是机器学习的过程。下面就详细的说一下决策数吧！

二、决策树的理论知识

1 什么叫决策树

决策树(decision tree) 是一类常见的机器学习方法，以二分类任务为例，我们希望从给定训练数据集学得一个模型用以对新示例进行分类，这个把样本分类的任务，可看作对"当前样本属于正类吗?“这个问题的"决策"或"判定"过程.顾名思义，决策树是基于树结构来进行决策的，这恰是人类在面临决策问题时一种很自然的处理机制。例如，我们要对"这是好瓜吗?“这样的问题进行决策时，通常会进行一系列的判断或"子决策"我们先看"它是什么颜色?”，如果是"青绿色”，则我们再看"它的根蒂是什么形态?"，如果是"蜷缩"，我们再判断"它敲起来是什么声音?"，最后我们得出最终决策:这是个好瓜。如下图。

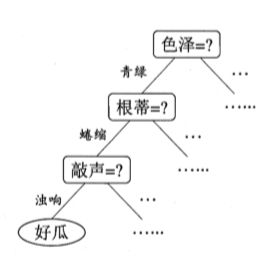
这时你可能会想：为什么一开始要先判断色泽呢？而不是敲声？这就涉及到了下节讲到的决策树的划分选择了。

2 决策树中的划分选择

在构造决策树时，我们需要解决的第⼀个问题就是，当前数据集上哪个特征在划分数据分类时起决定性作⽤（也就是在众多特征中找根节点，它的影响最大，然后再画它的子节点，影响稍微小点的特征，依次往下）。为了找到决定性的特征，划分出最好的结果，我们必须评估每个特征。完成测试之后，原始数据集就被划分为几个数据子集。这些数据⼦集会分布在第一个决策点的所有分支上。一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的"纯度" (purity)越来越高.
划分数据集的原则是：将无序的数据变得更加有序。我们可以使用多种方法划分数据集，但是每种⽅法都有各⾃的优缺点。在可以评测哪种数据划分⽅式是最好的数据划分之前，我们必须学习如何计算信息增益。

1). 信息增益

信息增益是在划分数据集之前之后信息发⽣的变化，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最⾼的特征就是最好的选择（就是我们要的根节点）。
“信息熵” (information entropy)是度量样本集合纯度最常用的一种指标. 假定当前样本集合 D 中第 k 类样本所占的比例为 Pk (k = 1,2,. . . , IyI)，则 D 的信息熵定义为

仔细看看这个公式，负号的位置为了好记忆是不是可以换换呀？

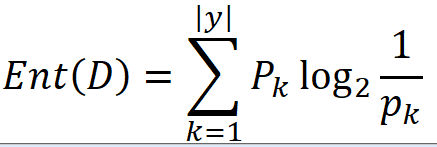
换一下位置不就成了概率乘log下概率的倒数了嘛？清爽很多了吧。这是总体样本的信息熵。那么一个属性各自取值的信息熵呢？就以有自己取值的所有样例作为一个集合，通过正反例算信息熵。最后乘各自的概率相加即可。
有了总体样本的信息熵，又求得了各自属性的信息熵，它们的信息增益直接相减即可得到。我们需要判断的是看哪个属性的信息增益大，大的就为决定性的因素。

语言是苍白的，关键时刻还得上例子。
现有如下数据集。

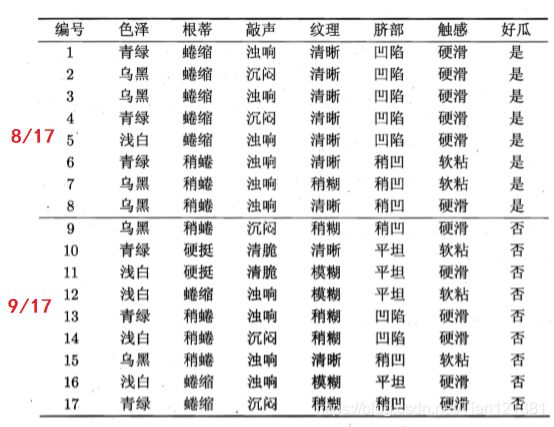
上图知数据集包含 17 个训练样例，用以学习一棵能预测设剖开的是不是好瓜的决策树.显然， IyI = 2（好坏瓜）。在决策树学习开始时，根结点包含 D 中的所有样例，其中好瓜的概率是8/17，坏瓜的是9/17。信息熵通过上述公式得。

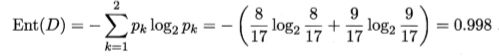
之后，我们要计算出当前属性集合{色泽，根蒂，敲声，纹理，脐部，触感} 中每个属性的信息增益。以属性"色泽"为例，它有 3 个可能的取值: {青绿，乌黑，浅白}。
先看取值青绿的集合，设为D1，它占总样本的6/17，其中共有6个样例，分别是编号 {1, 4, 6, 10, 13, 17} ，正例占 p1=3/6， 反例占p2=3/6；它的信息熵求的。

同理，用D2表示乌黑，D3表示浅白，得到它们信息熵为。

通过信息增益公式得。

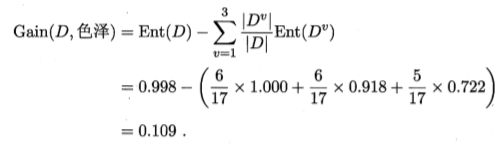
类似的，我们可计算出其他属性的信息增益:

显然，属性"纹理"的信息增益最大，于是它被选为划分属性.下图给出了基于"纹理"对根结点进行划分的结果，各分支结点所包含的样例子集显示在结点中。

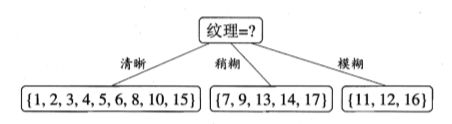
然后，决策树学习算法将对每个分支结点做进一步划分。以图上图中第一 个分支结点( “纹理=清晰” )为例，该结点包含的样例集合 D1 中有编号为 {1, 2, 3, 4, 5, 6, 8, 10, 15} 的 9 个样例，可用属性集合为{色泽，根蒂，敲声，脐部，触感}。基于 D1 计算出各属性的信息增益:

“根蒂”、 “脐部”、 “触感” 3 个属性均取得了最大的信息增益，可任选其中之一作为划分属性。类似的，对每个分支结点进行上述操作，最终得到的决策树如下图所示。

是不是觉得计算好复杂呀，没什么好担心得，一切交给计算机。<(￣ c￣)y▂ξ （面包会有的，下面的代码也会有的）

2). 增益率

在上面的介绍中，我们有意忽略了表中的"编号"这一列。若把"编号"也作为一个候选划分属性，则根据信息增益公式可计算出它的信息增益为 0.998， 远大于其他候选划分属性。这很容易理解"编号"将产生 17 个分支，每个分支结点仅包含一个样本，这些分支结点的纯度己达最大.然而，这样的决策树显然不具有泛化能力，无法对新样本进行有效预测。
实际上，信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，著名的 C4.5 决策树算法(看不看的吧，知道有这个东西就行啦)不直接使用信息增益，而是使用"增益率" (gain ratio) 来选择最优划分属性。采用信息增益公式相同的符号表示，增益率定义为

其中

IV(α)这个东西不就是信息熵嘛。
需注意的是，增益率准则对可取值数目较少的属性有所偏好，因此，它并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式 先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

3 剪枝处理

剪枝(pruning)是决策树学习算法对付"过拟合"的主要手段.在决策树学习中，为了尽可能正确分类训练样本，结点划分过程将不断重复，有时会造成决策树分支过多，这时就可能因训练样本学得"太好"了，以致于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合.因此，可通过主动去掉一些分支来降低过拟合的风险。
决策树剪枝的基本策略有"预剪枝" (prepruning)和"后剪枝"(post" pruning)。预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点；后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。
如何判断决策树泛化性能是否提升呢?这可使用了第一章介绍的性能评估方法。本节假定采用留出法，即预留一部分数据用作"验证集"以进行性能评估.例如西瓜数据集，我们将其随机划分为两部分，下表所示，编号为 {1，2，3，6，7，10，14，15，16，17} 的样例组成训练集，编号为 {4，5， 8，9，11，12，13} 的样例组成验证集。再来看一个实例吧！

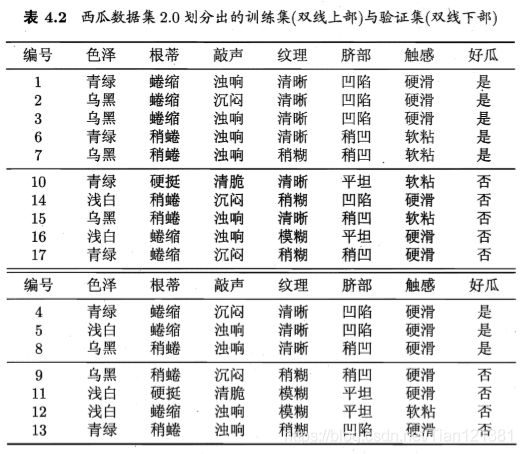
1). 预剪枝

我们先讨论预剪枝。基于信息增益准则，我们会选取属性"脐部"来对训练集进行划分，并产生 3 个分支。如下图。然而，是否应该进行这个划分呢?预剪枝要对划分前后的泛化性能进行估计。

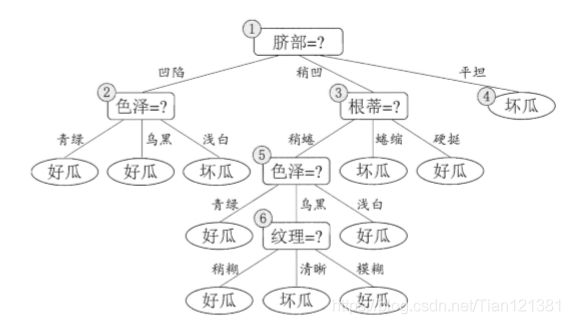
让我们来减一下吧！（图来源于致敬大神小姐姐）

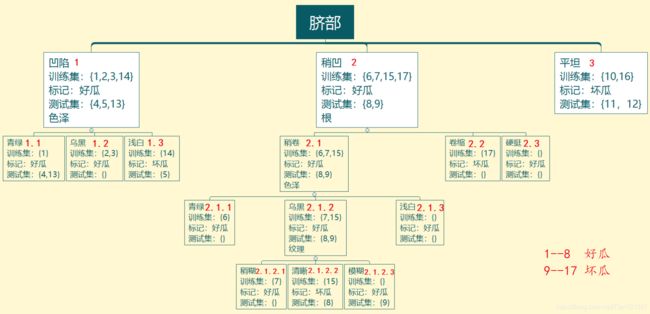
此图将各个属性的测试集，训练集样本序号全都标注上了，为了容易描述，我又给各属性加了序号。（注意样本序号，和节点标号呀！！！）
以脐部为例。脐部没有子节点时，它的正确率，就是测试集的正确率呗。3 / 7 = 42.9%（共7个测试集，3个正确的）。有序号为1 2 3的节点之后呢？分析一下，序号1的节点标记是好瓜（标记看训练集，那个标记数量多就是什么标记，如1节点中好瓜标记多，那它的标记就是好瓜），再看测试集，样本4，样本5正确。序号为2的节点，标记为好瓜，样本8正确。序号为3的节点中，标记是坏瓜，样本11，12都正确，这时7个样本对了2+1+2=5个，这时的精度就是5/7=71.4%了。划分后，精度提高了，也就不裁剪掉这些节点。
我现在的精度是71.4%了，也是说我判断是否裁剪掉第二代节点的子节点时，我划分前的精度为71.4%。以色泽为例。他是第二代节点，没有划分前是71.4%的精度。测试集中只有样本13错了。（这里不要用2 / 3 = 67%来求划分前的精度，要用上面求的71.4%）。划分后呢？
节点1.1标记好瓜，样本13错了。节点1.3中，标记是坏瓜，样本5错了。没划分前，错了一个，划分后还多错了一个，那它的精度就是
（5 - 1) / 7 = 57.1%，精度下降了，那就把它删去。如下图。

剩下的都是一样的做法的，可以自己看看。最终结果如下。

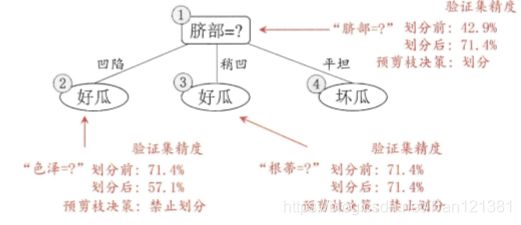
注： 精度相同的也裁剪，因为预剪枝的原则是：能减就减。

2). 后剪枝

后剪枝先从训练集生成一棵完整决策树，从后向前开始剪裁，它的原则是：能不减就不减。
还是那张图。

从下往上看（看所有的叶子节点）。以纹理（2.1.2）节点为例。裁剪之前：叶子节点1.1标记好瓜，样本4正确，样本13错误。没有样本的跳过。叶子节点1.3标记坏瓜，样本5错误。依次类推叶子节点2.1.1，2.1.2.1，2.1.2.2，2.1.2.3，2.1.3，2.2，2.3，3。得到共3个正确的，精度为3 / 7 = 42.9%。如果我裁剪掉纹理的子节点呢？（把2.1.2.x的挡着看）看所有叶子节点，1.1，1.2，1.3，2.1.1，2.1.2，2.1.3，2.2，2.3，3。正确的样本有4个，精度为4 / 7 = 57.1%。精度上升了，那么我们就裁掉它吧。值得注意的是别忘了后剪裁的原则，能不减就不减。所以相同精度的我是保留的。最后得如下图所示。

三、构造一个简单的决策树

1). 决策树的⼀般流程

• 收集数据：可以使⽤任何⽅法。
• 准备数据：树构造算法只适⽤于标称型数据，因此数值型数据必须离散化。
• 分析数据：可以使⽤任何⽅法，构造树完成之 后，我们应该检查图形是否符合预期。
• 训练算法：构造树的数据结构。
• 测试算法：使⽤经验树计算错误率。
• 使⽤算法：此步骤可以适⽤于任何监督学习算法，⽽使⽤决策树可以更好地理解数据的内在含义。

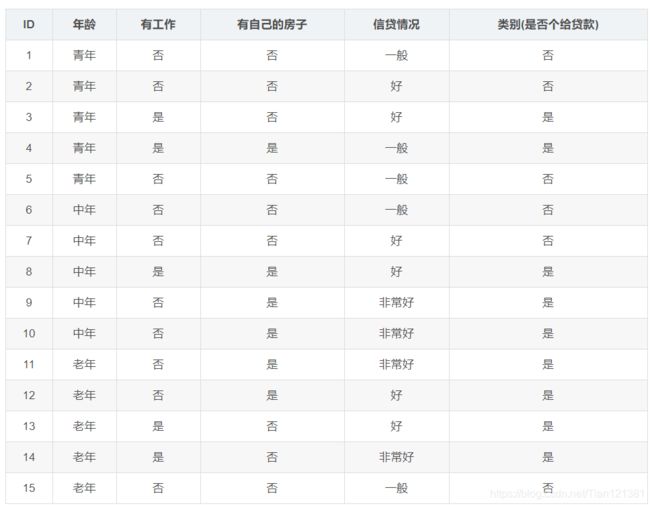
我们现有一组数据，里面有一个人的年龄，是否有工作，是否有房子，借贷信誉三个特征，标签是银行是否给他贷款，如图所示。

对数据集进行标注，为下面操作方便。

• 年龄：0代表青年，1代表中年，2代表老年；
• 有工作：0代表否，1代表是；
• 有自己的房子：0代表否，1代表是；
• 信贷情况：0代表一般，1代表好，2代表非常好；
• 类别(是否给贷款)：no代表否，yes代表是。

按照上表，咱们来写个简单的数据集吧！

2). 构造决策树

首先，引入相关包

"""
构建一个决策树
@Author:Yuuuuu、Tian
Fri Feb 14 10:40:06 2020
"""
from math import log
import operator
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

#创建数据集。

def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],         #数据集
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels = ['年龄','有工作','房子','信贷情况']
    return dataSet,labels

数据集咱们已经写好了，然后看看前面理论那里说的，一开始要先计算信息熵。

def calcShannonEnt(dateSet):
        numEntires = len(dateSet)
        labelCount = {}
        for featVec in dateSet:
                currentLabel = featVec[-1]   #获得标签
                labelCount[currentLabel] = labelCount.get(currentLabel,0) + 1      #统计各标签的数量
        #初始熵
        shannonEnt = 0
        for key in labelCount:
                prob = labelCount[key] / numEntires
                shannonEnt += -(prob * log(prob,2))   #信息熵公式
        return shannonEnt
#---------------测试--------------------------------------------------------------------
if __name__ == '__main__':
        dateSet,labels = createDataSet()
        shannonEnt = calcShannonEnt(dateSet)
        print(shannonEnt)

结果：

0.9709505944546686

信息熵求完后，我们就该计算一下信息增益，找到最优的特征了。
先引入一个信息增益的辅助函数，这个函数的主要功能是我们选了一个特征后，下面的叶子节点再分肯定就没这个特征取值了，目的就是去除这个特征取值，求剩下的特征矩阵。假设我们数据集中，已经分好了第2个特征（编号为1，数组嘛，第二列）值是0的了，下面我们继续划分要用那个数据集呢？对！就是咱们下面这个程序。

def splitDataSet(dataSet, axis, value):
    retDataSet = []                                        #创建返回的数据集列表
    for featVec in dataSet:                             #遍历数据集
        if featVec[axis] == value:
            #去掉中间数据，取前取尾
            reducedFeatVec = featVec[:axis]                #去掉axis特征
            reducedFeatVec.extend(featVec[axis+1:])     #将符合条件的添加到返回的数据集
            retDataSet.append(reducedFeatVec)
    return retDataSet
#-----测试------------------------------------------
dateSet,labels = createDataSet()
#我们数据集中，分好了第1个特征是0的了，下面我们用那个数据集继续划分呢？对！就是咱们运行完这个程序后的这个
a = splitDataSet(dateSet,1,0)  
print(a)
结果:

[[0, 0, 0, 'no'], 
[0, 0, 1, 'no'],
[0, 0, 0, 'no'], 
[1, 0, 0, 'no'], 
[1, 0, 1, 'no'], 
[1, 1, 2, 'yes'], 
[1, 1, 2, 'yes'],
[2, 1, 2, 'yes'], 
[2, 1, 1, 'yes'],
[2, 0, 0, 'no']]

去掉了所有第2个特征值是0的数据，剩下的矩阵如上。
看看结果，再看看前面的数据，理解一下。
然后开始信息增益啦。

#计算信息增益，求最优特征
def chooseBestFeatureToSplit(dataSet):
        #特征的数量，每个特征都要计算一下，求最大的。
        numFeateres = len(dataSet[0]) - 1   #减去标签，只剩数据
        #计算数据集总体的信息熵
        baseEntropy = calcShannonEnt(dataSet)
        #增益熵
        bestInfoGain = 0.0
        #假设最优的索引
        bestFeater = -1
        for i in range(numFeateres):
            #获取第i个特征的所有值
            featerlist = [example[i] for example in dataSet]
            uniqueVal = set(featerlist)    #去重
            #初始化经验熵
            newEntropy = 0
            for value in uniqueVal:
                subDataSet = splitDataSet(dataSet,i,value)
                prob = float(len(subDataSet) / len(dataSet))
                newEntropy += prob * (calcShannonEnt(subDataSet))    #计算各自特征分支节点的信息熵
            infoGain = baseEntropy - newEntropy    #增益熵
            print("第",i+1,"个增益熵是：",infoGain)
            if(infoGain > bestInfoGain):   #求最大信息熵
                bestInfoGain = infoGain 
                bestFeater = i
        return bestFeater   #返回最大信息熵的位置
#--------测试---------------------------------------------------------------
if __name__ == '__main__':
    dataSet, features = createDataSet()
    print("最优特征索引值:" + str(chooseBestFeatureToSplit(dataSet)))

结果：

	第 1 个增益熵是： 0.08300749985576883
	第 2 个增益熵是： 0.32365019815155627
	第 3 个增益熵是： 0.4199730940219749
	第 4 个增益熵是： 0.36298956253708536
	最优特征索引值:2

对比我们自己计算的结果，发现结果完全正确！最优特征的索引值为2，也就是特征3(有自己的房子)。
信息增益都求完了，那就构造决策树的主体部分呗。

#统计classList中出现此处最多的元素(类标签)
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        classCount[vote] = classCount.get(vote,0) + 1    #统计各值的数量
    #排序选数值最大的，就像前面西瓜的那个例子，选训练集值得数量最多的为它的值  
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)   
    return sortedClassCount[0][0]   
    
#创建决策树
def createTree(dataSet,labels,featLabels):
	#取出全部标签
    classList = [example[-1] for example in dataSet]
    #递归几次后，剩下的类别如果全部相等，则停止递归，因为不能再分了呀。
    if classList.count(classList[0]) == len(classList):   
        return classList[0]
    #遍历完所有特征，只剩下一个了，返回特征里值数量多的那个值。
    if len(dataSet[0]) == 1:  
        return majorityCnt(classList)    #返回出现特征值多的
    #选择最优特征
    bestFeat = chooseBestFeatureToSplit(dataSet)   #返回的是数组位置
    #最优的标签
    bestFeatLabel = labels[bestFeat]
    featLabels.append(bestFeatLabel)  #加入特征标签列表
    #根据最优标签，生成树
    myTree = {bestFeatLabel:{}}    #注意字典的结构。
    featValues = [example[bestFeat] for example in dataSet]  #得到训练集中所有最优特征的属性值
    uniqueVals = set(featValues)  #删除重复的
    for value in uniqueVals:
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),labels,featLabels) #递归
    return myTree
#----------测试------------------------------------------------------------
if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet,labels,featLabels)
    print(myTree)

结果：（最优的包着第二优的，第二优的包着第三优的，没有的就是不值得分的了）

	{'房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}

3). 使用Matplotlib 注解绘制树形图----小例子

这节使⽤Matplotlib的注解功能绘制树形图，它可以对⽂字着⾊并提供多种形状以供选择，⽽且我们还可以反转箭头，将它指向⽂本框⽽不是数据点。在画上面决策树图之前，我们先来看一个小例子，这里用到了annotate（）函数，具体参数如下。
create_plot.ax1.annotate(node_txt, xy=parent_pt, xycoords=‘axes fraction’, xytext=center_pt,
textcoords=‘axes fraction’, va=“center”, ha=“center”, bbox=node_type, arrowprops=arrow_args)

• node_txt: 节点的名字；
• centerPt表示那个节点框的位置。
• parentPt表示那个箭头的起始位置。
• xy: 被注解的东西的位置，在决策树中为上一个节点的位置
• xycoords:被注解的东西依据的坐标原点位置，是以图像还是坐标轴,参考点
• xytext: 注解内容的中心坐标
• textcoords:注解内容依据的坐标原点位置
• va: horizontal alignment 文本中内容竖向对齐方式
• ha: vertical alignment 文本中的内容 横向对齐方式
• arrowprops: 标记线的类型，是一个字典，如果字典中包含key为arrowstyle的，则默认类别有’->'等
• bbox: 对方框的设置

代码如下，具体看注释吧！

import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
#定义文本框和箭头的格式
decisionNode = dict(boxstyle = "sawtooth",fc = '0.8')
leafNode = dict(boxstyle = "round4",fc = '0.8')
arrow_arg = dict(arrowstyle = "<-")
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)        #设置中文字体
#描绘带箭头的注解
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
    #创建一个新框 ，annotate 注释的意思
    createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext = centerPt,
                            textcoords = 'axes fraction',va = 'center',ha = 'center',
                            bbox = nodeType,arrowprops = arrow_arg,FontProperties = font)
def createPlot():
    fig = plt.figure(1,facecolor='white')
    fig.clf()   # 将画图清空
    createPlot.ax1 = plt.subplot(111,frameon = False) # 设置一个多图展示，但是设置多图只有一个
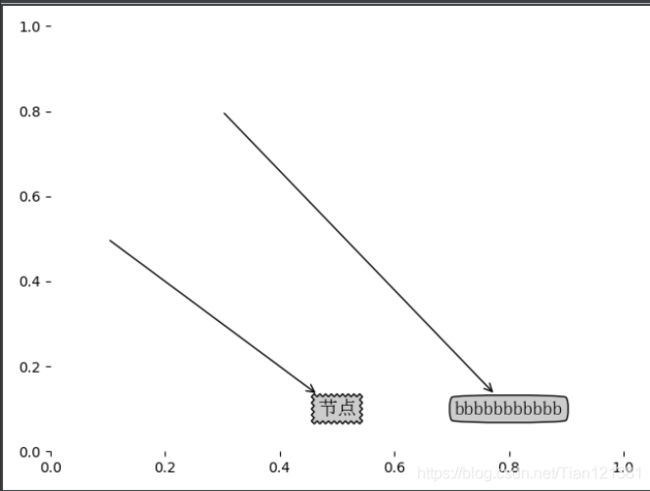
    plotNode('决策节点',(0.5,0.1),(0.1,0.5),decisionNode)
    plotNode('叶子节点',(0.8,0.1),(0.3,0.8),leafNode)
    plt.show()
createPlot()

结果：

4). 使用Matplotlib绘制决策树

可视化需要用到的函数：

• getNumLeafs：获取决策树叶子结点的数目
• getTreeDepth：获取决策树的层数
• plotNode：绘制结点
• plotMidText：标注有向边属性值
• plotTree：绘制决策树
• createPlot：创建绘制面板

接下来就依次写一下这些函数。
获取决策树叶子结点的数目。思路：通过判断是否是字典类型，是字典的话，则也是一个判断点，不是的话，就是叶子节点。

def getNumLeafs(myTree):
    numLeafs = 0
    # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性，
    # 可以使用list(myTree.keys())[0]
    firstStr = list(myTree.keys())[0]
    #获取下一组字典
    secondDict = myTree[firstStr]   #获取下一组字典
    #print(secondDict.keys())
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':  # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            numLeafs += getNumLeafs(secondDict[key])
            #print(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs
#--------------测试---------------------------------------------
if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    print(myTree)
    numLeafs = getNumLeafs(myTree)
    print(numLeafs)

结果：

3

获取决策树的层数。

def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    #thisDepth = 1
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        # 测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
        #print(secondDict.keys())
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
            # print(thisDepth)
            # print(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:maxDepth = thisDepth
    return maxDepth
#----------测试--------------------------------------------------
if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    #print(myTree)
    depth = getTreeDepth(myTree)
    print("深度：",depth)

结果：

	深度： 2

绘制节点。

def plotNode(nodeTxt,centerPt,parentPt,nodeType):
    # 定义箭头格式
    arrow_arg = dict(arrowstyle = '<-')
    # 设置中文字体
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    # 绘制结点
    #创建一个新框，用到了上面小例子里的函数。
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt,
                            textcoords='axes fraction', va='center', ha='center',
                            bbox=nodeType, arrowprops=arrow_arg,FontProperties = font)

标注有向边的属性值

def plotMidText(cntrPt,parentPt,txtString):
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    createPlot.ax1.text(xMid,yMid,txtString,va = 'center',ha = 'center',rotation = 30)

描绘决策树

def plotTree(myTree, parentPt, nodeTxt):
    decisionNode = dict(boxstyle="sawtooth", fc="0.8")         #设置结点格式
    leafNode = dict(boxstyle="round4", fc="0.8")               #设置叶结点格式
    numLeafs = getNumLeafs(myTree)                             #获取决策树叶结点数目，决定了树的宽度
    depth = getTreeDepth(myTree)                               #获取决策树层数
    firstStr = list(myTree.keys())[0]                          #下个字典
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)    #中心位置
    plotMidText(cntrPt, parentPt, nodeTxt)                     #标注有向边属性值
    plotNode(firstStr, cntrPt, parentPt, decisionNode)         #绘制结点
    secondDict = myTree[firstStr]                              #下一个字典，也就是继续绘制子结点
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD        #y偏移
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':             #测试该结点是否为字典，如果不是字典，代表此结点为叶子结点
            plotTree(secondDict[key],cntrPt,str(key))          #不是叶结点，递归调用继续绘制
        else:                                                  #如果是叶结点，绘制叶结点，并标注有向边属性值
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

创建绘制面板

def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')         #创建fig
    fig.clf()                                      #清空fig
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)      #去掉x、y轴
    plotTree.totalW = float(getNumLeafs(inTree))                     #获取决策树叶结点数目
    plotTree.totalD = float(getTreeDepth(inTree))                    #获取决策树层数
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;       #x偏移
    plotTree(inTree, (0.5,1.0), '')                                  #绘制决策树
    plt.show()                                                       #显示绘制结果
#看一下咱们的决策树吧！
#--------测试---------------------------
if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    print(myTree)
    createPlot(myTree)

看出来了，银行贷不贷款和年龄没关系呀。
是不是看到画图的有些懵逼呀，一个图还要写这么多函数。放心，决策树图画法有更简单的方法（下个实例讲）Hi~ o(￣▽￣)ブ

5). 使用决策树

依靠训练数据构造了决策树之后，我们可以将它⽤于实际数据的分类。在执⾏数据分类时，需要决策树以及⽤于构造树的标签向量。然后，程序⽐较测试数据与决策树上的数值，递归执行该过程直到进⼊叶子节点；最后将测试数据定义为叶子节点所属的类型。 代码实现一下吧！

def classify(inputTree,featLabels,testVec):
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__ == 'dict':     
                classLabel = classify(secondDict[key], featLabels, testVec)   #依次递归，直到叶子节点。
            else:
                classLabel = secondDict[key]
    return classLabel

------测试---------------------

if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    myTree = createTree(dataSet, labels, featLabels)
    testVec = [0,1]            #测试数据   （没房子 有工作）
    result = classify(myTree, featLabels, testVec)
    if result == 'yes':
        print('放贷')
    if result == 'no':
        print('不放贷')

结果：

放贷

四、实例-使用决策树预测隐形眼镜类型 （SKlearn）

本节我们将通过⼀个例⼦讲解决策树如何预测患者需要佩戴的隐形眼镜类型。使⽤小数据集，我们就可以利⽤决策树学到很多知识：眼科医⽣是如何判断患者需要佩戴的镜片类型；⼀旦理解了决策树的⼯作原理，我们甚至也可以帮助⼈们判断需要佩戴的镜⽚类型。

1). 理论流程

使用决策树预测隐形眼镜类型流程：

1. 收集数据：置顶资料下载处。
2. 准备数据：分隔的数据行。
3. 分析数据：快速检查数据，确保正确地解析数据内容，绘制最终的树形图。
4. 训练算法：使⽤sklearn的模块。
5. 测试算法：编写测试函数验证决策树可以正确分类给定的数据实例。
6. 使⽤算法：存储树的数据结构，以便下次使用时 无需重新构造树。

2). 前提小知识

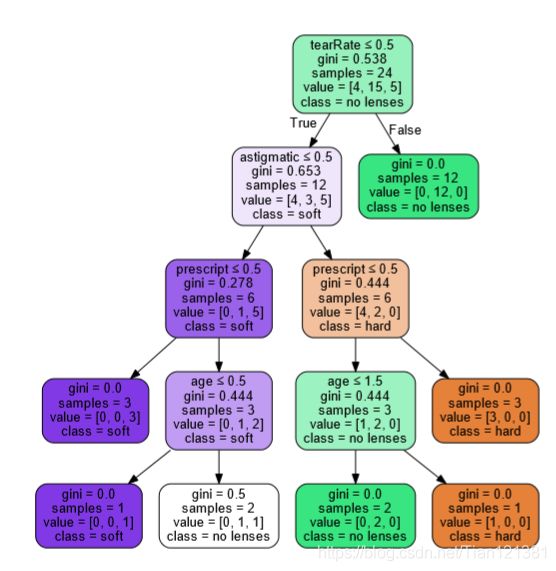
隐形眼镜数据集1是⾮常著名的数据集，它包含很多患者眼部状况的观察条件以及医⽣推荐的隐形眼镜类型。隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。数据来源于UCI数据库，为了更容易显示数据，本节对数据做了简单的更改，数据存储在源代码下载路径的⽂本⽂件中。一共有24组数据，数据的Labels依次是age、prescript、astigmatic、tearRate、class，也就是第一列是年龄，第二列是症状，第三列是是否散光，第四列是眼泪数量，第五列是最终的分类标签。
此实战使用的是sklearn的DecisionTreeClassifier函数，用于决策树的构造。
我给出了sklearn的官方文档，可以详细的看看这个函数中参数解释。
slearn中决策树的介绍，简单的小例子。
可视化工具我们使用了 export_graphviz。它的操作需要先下载包：pydotplus。

然后安装Graphviz，安装包在我置顶资料下载处，安装完成后还需要坏境变量的配置。

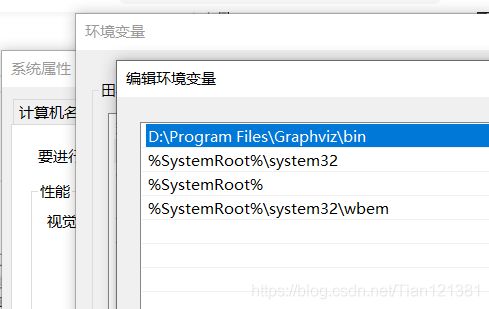
环境：Path = 安装路径\Graphviz\bin    
注意：装完还要重启IDE，不然会报GraphViz's executables not found

fit()函数不能接收string类型的数据，通过打印的信息可以看到，数据都是string类型的。在使用fit()函数之前，我们需要对数据集进行编码。
我用的是LabelEncoder函数，它可以将标签分配一个0—n_classes-1之间的编码，如下。

为了对string类型的数据序列化，需要先生成pandas数据，这样方便我们的序列化工作。这里我使用的方法是，原始数据->字典->pandas数据，pd.DataFrame()函数解析
所用到的小知识点就这些，开始代码编写(ง •_•)ง。

3). 代码编写

详看注释(￣︶￣*))，我自己测试的print()没删，不理解的话，可以print()一下，看看输出情况。
导入相关库。

"""
使用Sklearn实战一个决策树预测隐形眼镜的类型
@Author:Yuuuuu、Tian
Sun Feb 16 15:24:59 2020
"""
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.externals.six import StringIO
from sklearn import tree
import pandas as pd
import numpy as np
import pydotplus

决策树主体代码。

if __name__ == "__main__":
    fr = open('0503 decision_tree_Sklearn/lenses.txt')   
    lenses = [inst.strip().split('\t') for inst in fr.readlines()]
    lenses_target = []  #提取每组数据的类别，保存在列表里
    #print(lenses)
    for each in lenses:
        lenses_target.append(each[-1])   
    #特征标签
    lensesLabels = ['age','prescript','astigmatic','tearRate']
    lenses_list = []  #保存lenses数据的临时列表
    lenses_dict = {}  #保存lenses数据的字典，用于生成pandas
    for each_label in lensesLabels:
        for each in lenses:
            lenses_list.append(each[lensesLabels.index(each_label)])
            #print('aaa',lenses_list)
        #print('ddd',each_label)
        lenses_dict[each_label] = lenses_list
        # print('ccc:', lenses_dict[each_label])
        # print('bbb',lenses_list)
        lenses_list = []   #置0循环
    #print('ccc:',lenses_dict)
    #pd.DataFrame(数据, index=list('行表'), columns=list('列表C'))
    #使用字典创建 pd.DataFrame(dic1)
    lenses_pd = pd.DataFrame(lenses_dict)
    print(lenses_pd)
    le = LabelEncoder()  #创建LabelEncoder()对象，用于序列化。 将字符串转换为增量值
    for col in lenses_pd.columns:  ##为每一列序列化
        lenses_pd[col] = le.fit_transform(lenses_pd[col])   #处理数据
    print(lenses_pd)
    clf = tree.DecisionTreeClassifier(max_depth=4)  # 创建DecisionTreeClassifier()类，我们只定义了树的深度。
    clf = clf.fit(lenses_pd.values.tolist(), lenses_target)  #拟合，构建决策树   tolist()将数组或者矩阵转换成列表
    #绘制图像
    dot_data = StringIO()
    #print('qqq:',lenses_pd.keys())
    #print('www:',clf.classes_)
    tree.export_graphviz(clf, out_file=dot_data,  # 绘制决策树
                         feature_names=lenses_pd.keys(),  #属性
                         class_names=clf.classes_,   #结果
                         filled=True, rounded=True,
                         special_characters=True)
    graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
    graph.write_pdf("tree.pdf")   #讲图输出
    #----测试-----------------------预测结果
    print('1,1,1,0的预测：',clf.predict([[1,1,1,0]]))

结果：

	1,1,1,0的预测： ['hard']

以上就是我理解的决策树的所有内容了。

五、总结

讲了决策树，那决策树的优缺点就不能不说了。
决策树的优点：

• 易于理解和解释。树木可以可视化。
• 需要很少的数据准备。其他技术通常需要数据规范化，需要创建伪变量并删除空白值。但是请注意，此模块不支持缺少的值。
• 使用树的成本（即预测数据）与用于训练树的数据点数量成对数。
• 能够处理数字和分类数据。其他技术通常专用于分析仅具有一种类型的变量的数据集。
• 能够处理多输出问题。
• 使用白盒模型。如果模型中可以观察到给定的情况，则可以通过布尔逻辑轻松解释条件。相反，在黑匣子模型中（例如，在人工神经网络中），结果可能更难以解释。
• 可以使用统计测试来验证模型。这使得考虑模型的可靠性成为可能。
• 即使生成数据的真实模型在某种程度上违反了它的假设，也可以表现良好。

决策树的缺点：

• 决策树学习者可能会创建过于复杂的树，从而无法很好地概括数据。这称为过度拟合。为避免此问题，必须使用诸如修剪（当前不支持），设置叶节点处所需的最小样本数或设置树的最大深度之类的机制。
• 决策树可能不稳定，因为数据中的细微变化可能会导致生成完全不同的树。通过使用集成中的决策树可以缓解此问题。
• 有些概念很难学习，因为决策树无法轻松表达它们，例如XOR，奇偶校验或多路复用器问题。
• 如果某些类别占主导地位，决策树学习者会创建有偏见的树。因此，建议在与决策树拟合之前平衡数据集。

第2章、第3章讨论的是结果确定的分类算法，数据实例最终会被明确划分到某个分类中。下⼀章我们讨论的分类算法将不能完全确定数据实例应该划分到某个分类，或者只能给出数据实例属于给定分类的概概率。下章----贝叶斯分类器见(。・∀・)ノ

• 本文结合各位大牛所思所想，不胜感激！
• 如有错误，请不吝指正！
• 喜欢的请点赞呀(★ ω ★)