基于seed数据集的脑电情绪识别(附论文和源码)(改进的循环神经网络(简单循环单元神经网络)和集成学习)并提取了微分熵、功率谱等特征
论文和源码链接见个人主页:基于seed数据集的脑电情绪识别(附论文和源码)(改进的循环神经网络和集成学习)并提取了微分熵、功率谱等特征。
https://download.csdn.net/download/qq_45874683/83935782
介绍一篇2020年的基于seed数据集的脑电情绪识别的论文
摘要
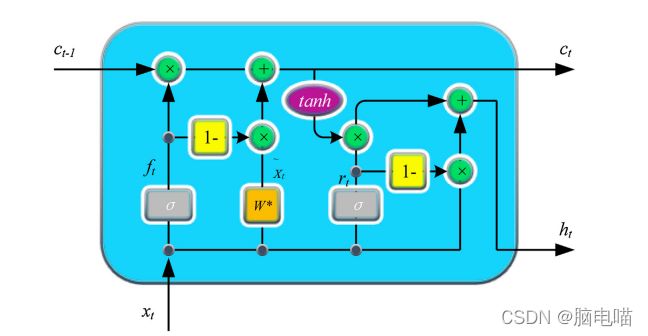
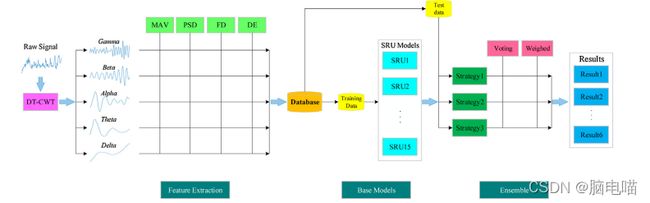
本研究的目的是开发一个基于脑电图的情绪识别系统,用于识别三种情绪:积极情绪、中性情绪和消极情绪。到目前为止,各种用于自动情感识别的建模方法已经被报道。然而,情感过程中的时间依赖性并没有得到充分考虑。为了掌握脑电的时间信息,我们采用了深度循环(SRU)神经网络,该网络不仅能够处理序列数据,而且能够解决常规循环神经网络(RNN)中长期依赖的问题。在训练情绪模型之前,采用双树复小波变换(DT-CWT)将原始脑电信号分解为五个子带,然后利用时间、频率和非线性分析从中提取特征。接下来,利用五个频带上的四种不同特征(功率谱密度和微分熵等特征)建立了深层SRU模型,发现良好的结果与更高的频带有关。最后,采用三种集成策略对基本SRU模型进行集成,以获得更理想的分类性能。我们评估和比较了浅层模型、深层模型和集成模型的性能。实验结果表明,基于SRU网络和集成学习的情感识别系统能够以相对经济的计算成本获得满意的识别性能。最终准确率达到80%。
首先将seed数据集划分为三种情绪类型,积极、中性和消极。(SEED数据集包含15名受试者观看4分钟电影片段时的脑电信号)
本论文使用的主要方法:
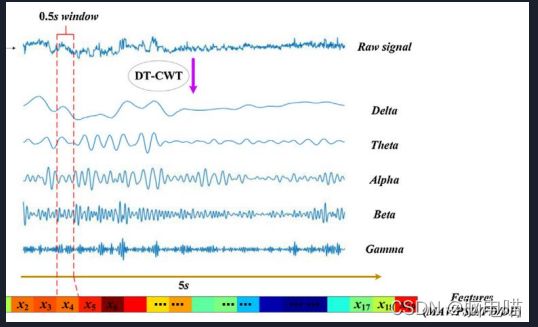
● 使用DT-CWT进行脑电信号数据预处理。
● 利用分解后的脑电信号进行特征提取。
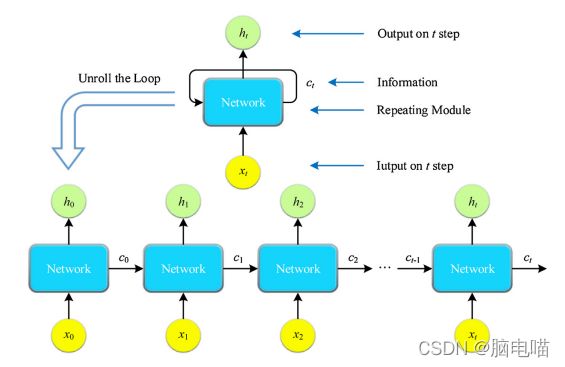
● 使用SRU建立模型。
● 整体学习
本论文所提取的特征:
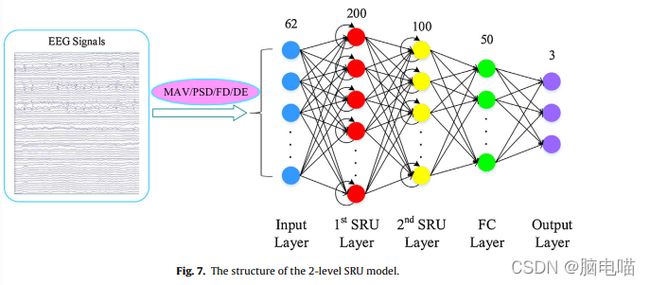
1.时域特征:时间分析(平均绝对值)(MAV)
2.频域特征:频率分析(功率谱密度)(PSD)
3.时频域特征:复杂性分析(分形维数和微分熵)(FD 和 DE)
训练方法:
● 每个特征提取以19个时间间隔进行,为每个EEG信号生成19个时间步长。
● 每个EEG信号的62个通道作为模型的特征。
● 对每个DTCWT分解信号提取四种特征,并将其转换为19个序列长度。
● 每个样本的数据分为15部分,前9部分用于训练集,后面6部分用于测试,
数据维度:训练数据(19,9,62)和测试数据(19,6,62)(时间步、样本、特征)
模型图:
循环神经网络(RNN):
改进的循环神经网络:
二重的改进模型:
实验的完整步骤:
最终结果:
部分代码解析:
DC-TWT:
transform = dtcwt.Transform1d()
for row in range(data.shape[0]):
for col in data.columns:
#checking if size of eeg_data is even
if(len(data.loc[row,col])%2!=0):
eeg_data=np.array(data.loc[row,col][:-1])
else:
eeg_data=np.array(data.loc[row,col])
vecs_t = transform.forward(eeg_data, nlevels=5)
data_dtcwt_delta.loc[row,col]=vecs_t.highpasses[0]
data_dtcwt_theta.loc[row,col]=vecs_t.highpasses[1]
data_dtcwt_alpha.loc[row,col]=vecs_t.highpasses[2]
data_dtcwt_beta.loc[row,col]=vecs_t.highpasses[3]
data_dtcwt_gamma.loc[row,col]=vecs_t.highpasses[4]
data_dtcwt.loc[row,col]= transform.inverse(vecs_t) 功率谱密度(PSD):
psd_delta=data_dtcwt_delta.copy()
psd_theta=data_dtcwt_theta.copy()
psd_alpha=data_dtcwt_alpha.copy()
psd_beta=data_dtcwt_beta.copy()
psd_gamma=data_dtcwt_gamma.copy()
# print(psd_delta.iloc[0,0][0:5])
psds=[psd_delta,psd_theta,psd_alpha,psd_beta,psd_gamma]
for (psd,data_) in zip(psds,data_dtcwt_list):
for row in range(data.shape[0]):
for col in data.columns:
#Get the eeg signal
sig=data_.loc[row,col]
#Calculate Power Spectral Density
PSD=[]
length=int(np.ceil(psd.loc[row,col].shape[0]/19))
for i in range(psd.loc[row,col].shape[0]//length+1):
psd_batch=np.mean(sig[length*i:length*(i+1)]*np.conj(sig[length*i:length*(i+1)]))/length
PSD.append(psd_batch)
PSD=np.array(PSD).astype('complex128')
# print(PSD.shape)
psd.loc[row,col]=PSD
# psd.shape
# psd_delta.shape微分熵(DE):
from scipy.stats import entropy
entropy_delta=data_dtcwt_delta.copy()
entropy_theta=data_dtcwt_theta.copy()
entropy_alpha=data_dtcwt_alpha.copy()
entropy_beta=data_dtcwt_beta.copy()
entropy_gamma=data_dtcwt_gamma.copy()
# print(entropy_delta.iloc[0,0][0:5])
entropys=[entropy_delta,entropy_theta,entropy_alpha,entropy_beta,entropy_gamma]
for (ent,data_) in zip(entropys,data_dtcwt_list):
for row in range(data.shape[0]):
for col in data.columns:
#Get the eeg signal
sig=data_.loc[row,col]
ENTROPY=[]
length=int(np.ceil(ent.loc[row,col].shape[0]/19))
for i in range(ent.loc[row,col].shape[0]//length+1):
#Get the eeg signal
sig_batch=np.real(sig[length*i:length*(i+1)])
sig_batch=np.squeeze(sig_batch)
pd_series = pd.Series(sig_batch)
#Get count of each value for calculating probabilty for entropy
counts = pd_series.value_counts()
#Calculate Entropy
entropy_batch = entropy(counts)
ENTROPY.append(entropy_batch)
# print(entropy.shape)
ENTROPY=np.array(ENTROPY)
ent.loc[row,col]=ENTROPY
entropy_delta.shape论文和源码链接见个人主页:基于seed数据集的脑电情绪识别(附论文和源码)(改进的循环神经网络和集成学习)并提取了微分熵、功率谱等特征。
https://download.csdn.net/download/qq_45874683/83935782