ST电机库的FOC部分解读笔记

1.前言

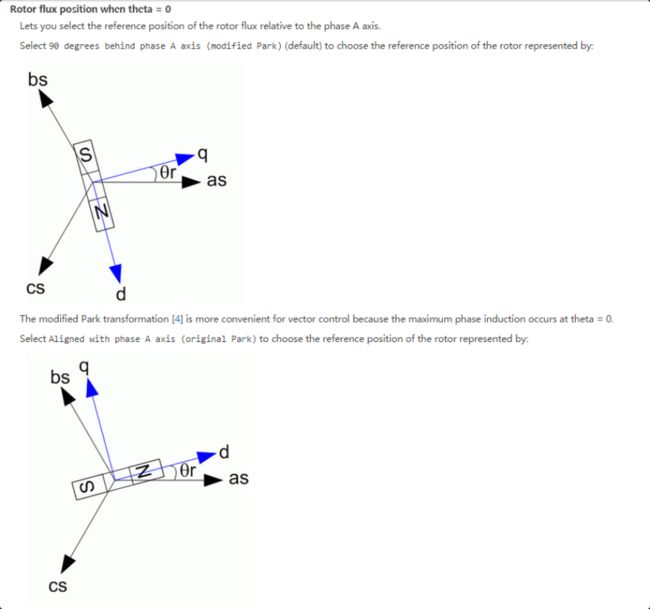
​ 如下图所示为ST培训资料的PPT中进行定义的坐标系，图中可以看出和常见的坐标系定义不同的主要有两点：

• ST定义的beta轴朝下，而常见的定义beta轴是朝上的。这个定义和欧洲人习惯定义y轴朝下有关，这个只会影响Clarke变换，让beta轴的结果和常见的结果差一个负号；
• ST定义的电角度theta是q轴和alpha轴的夹角，而常见的定义是d轴和alpha轴的夹角。这个会导致Park变换的结果和常见的结果完全相反（交换dq轴），实际上物理效果是一样的。

2.Clarke变换

1. 已解决：Clarke变换的函数比较容易看明白，问题也不是很大，由于没有涉及到电角度theta，所以结果只是beta轴的结果和常见的结果差一个负号。并且注意ST的Clarke变换中前面×了系数2/3。
2. 遗留：程序中第41行的问题，为什么要在最小值的地方限幅修改？此时其实并没有溢出，而且这个改动值也很小。

// Clarke变换问题不是很大，主要注意两点：
// 1.Clark变换中前面×了系数2/3
// 2.建立的坐标系alpha和常见的一样，但是beta坐标系是朝下的，所以和一般的结果差一个负号
alphabeta_t mc_clark(ab_t input)
{
	alphabeta_t output;

	int32_t a_divSQRT3_tmp, b_divSQRT3_tmp ;
	int32_t wbeta_tmp;
	int16_t hbeta_tmp;

	/* qIalpha = qIas*/
	output.alpha = input.a;  // 注意这里的clarke变换×了系数2/3

	a_divSQRT3_tmp = divSQRT_3 * ( int32_t )input.a;

	b_divSQRT3_tmp = divSQRT_3 * ( int32_t )input.b;

	/*qIbeta = -(2*qIbs+qIas)/sqrt(3)*/   // 这里是负的，也就是beta轴是朝下的
	wbeta_tmp = ( -( a_divSQRT3_tmp ) - ( b_divSQRT3_tmp ) -
	( b_divSQRT3_tmp ) ) >> 15;  
	// 这里>>15是因为上面是两个Q15格式的数据进行运算，结果是Q30格式，需要重新转换为Q15格式


	/* Check saturation of Ibeta */
	if ( wbeta_tmp > INT16_MAX )  // INT16_MAX = 32767
	{
		hbeta_tmp = INT16_MAX;
	}
	else if ( wbeta_tmp < ( -32768 ) )
	{
		hbeta_tmp = ( -32768 );
	}
	else
	{
		hbeta_tmp = ( int16_t )( wbeta_tmp );
	}

	output.beta = hbeta_tmp;

	// 这里的限幅是干什么的？把-32768限幅成-32767?
	if ( output.beta == ( int16_t )( -32768 ) )
	{
		output.beta = -32767;
	}

	return ( output );
}

3.Park和Rev-Park变换

3.1.不同的坐标系定义

​ Park（Rev-Park）变换应该是ST的电机库比较难理解的一点，因为程序的运算结果和常见的推导结果完全相反（交换了dq轴的结果）。这里和1.前言中说的ST的坐标定义有关。有关坐标定义，可以参照 FOC中坐标系和电角度的定义 。

​ 如果按照这个坐标系定义，又会出现一个难以理解的问题，因为常见的电角度定义为d轴和alpha轴的夹角，为什么这里定义为q轴和alpha轴的夹角也可以呢？这样结果不会出错吗？

​ 实际上，解答这个问题还是要从FOC的核心思想上来解答。FOC使用Clarke变换和Park变换是为了什么？就是为了生成超前转子（d轴，注意不论电角度怎么定义，dq轴定义总是不变的）90度的磁场，或者说超前转子90度的电流。那么电角度theta有什么用呢？其实它仅仅是为了指示当前转子在什么方向，从而生成一个超前转子90度的磁场，因为abc轴和alpha/beta轴都是固定的，而只有知道要生成的磁场相对这些固定的坐标轴在什么位置，才能进行在旋转坐标轴和固定坐标轴之间相互转换。所以说，电角度可以随便定义，它可以是q轴和alpha的夹角，也可以是d轴和alpha的夹角，甚至可以是d轴和（alpha轴与beta轴）的角平分线的夹角，因为电角度存在的意义只是为了指示当前转子在什么方向，然后生成一个超前转子90度的磁场，利用电角度，就可以把这个磁场分解到固定的坐标轴上去，然后控制PWM的生成。

​ 那么为什么常见的定义是d轴或者q轴和alpha轴的夹角呢？其实很简单，就是为了Park和反Park变换的方便，因为此时只需要在dq轴和alpha/beta轴之间相互投影即可，而投影的时候×的系数就是theta的三角函数值。由此看来，这个夹角定义成d轴或者q轴和beta轴的夹角也是可以的，它同样方便计算。但是如果定义成和其他轴（比如alpha和beta角平分线）的夹角，那么投影计算的时候就不好算了。

​ 总之记住：**所有的变换最终结果都是为了生成超前转子90度的磁场，而电角度只是为了提供转子的位置，方便磁场在各个坐标系之间进行变换。**这也是FOC的核心思想！

3.2.为什么给-90度电角度就能进行电角度预校准?

​ 参考解答

​ 为什么要进行电角度校准呢？也很简单，因为电机初始停在任意的一个位置，此时磁编码器是有一个读数的（而且极大的概率不是0）。但是从上面常见的坐标系的定义可以直到，电角度的零度是q轴或者d轴与alpha轴对齐的时候定义为电角度0度，此时编码器读出来的角度再×极对数就是偏置电角度。后面读取电角度的时候，只需要把编码器实际读出来的机械角度转换为电角度，然后再减去极对数，就是真正的电角度了。这里也可以发现，由于P对极的电机在初始对齐的时候可以有P个位置，也就对应有P个偏置电机度，实际上使用哪个偏置电角度都可以。（详见另一篇笔记）

​ 为什么给-90度电角度就能进行电角度预校准？答案还是和FOC的核心思想有关，那就是FOC控制要生成一个超前转子90度的磁场。

3.2.1.电角度定义为d轴和alpha轴的夹角

​ 如下图所示，电角度定义为d轴和alpha轴的夹角，此时为了校准电角度，也就是找到电角度0度的位置，那么要让d轴和alpha轴对齐，这个时候的电角度就是0度。为了让d轴和alpha轴对齐，那么就要生成alpha轴方向的磁场。由于是使用FOC控制，其核心就是控制生成一个超前转子90度的磁场，那么此时虚拟的转子应该在滞后alpha轴90度的方向，也就是在校准电角度的时候角度的反馈不是编码器来的，而是人为给定的，因为目的就是要生成一个想要的固定方向的磁场，从而吸引转子到这个方向，从而对齐电角度0度。所以此时虚拟的转子在图示位置，d轴也在这个位置，那么电角度是d轴和alpha轴的夹角，由图可知就是-90度。

3.2.2.电角度定义为q轴和alpha轴的夹角

​ 如下图所示，电角度定义为q轴和alpha轴的夹角，此时为了校准电角度，也就是找到电角度0度的位置，那么要让q轴和alpha轴对齐，这个时候的电角度就是0度。为了让q轴和alpha轴对齐，那么就要生成beta轴方向的磁场。由于是使用FOC控制，其核心就是控制生成一个超前转子90度的磁场，那么此时虚拟的转子应该在滞后beta轴90度的方向，也就是在校准电角度的时候角度的反馈不是编码器来的，而是人为给定的，因为目的就是要生成一个想要的固定方向的磁场，从而吸引转子到这个方向，从而对齐电角度0度。所以此时虚拟的转子在图示位置，d轴也在这个位置，此时的q轴在生成的FOC磁场的方向，那么电角度是q轴和alpha轴的夹角，由图可知电角度就是-90度。

// Park变化问题比较大，目前还没有弄明白
// 解决！终于明白了这里的Park变换为什么不对了！
// 坐标系的定义：https://www.cnblogs.com/neriq/p/14800876.html
qd_t mc_park(alphabeta_t input, int16_t theta)
{
	qd_t output;
	int32_t d_tmp_1, d_tmp_2, q_tmp_1, q_tmp_2;
	trig_components local_vector_components;
	int32_t wqd_tmp;
	int16_t hqd_tmp;

	// 计算输入的角度的sin和cos值
	local_vector_components = mc_trig_functions(theta);

	/*No overflow guaranteed  无溢出保证*/
	q_tmp_1 = input.alpha * ( int32_t )local_vector_components.h_cos;

	/*No overflow guaranteed  无溢出保证*/
	q_tmp_2 = input.beta * ( int32_t )local_vector_components.h_sin;

	/*Iq component in Q1.15 Format */
	wqd_tmp = ( q_tmp_1 - q_tmp_2 ) >> 15;  // 这里就是在算iq
	// 注意这里>>15为还是因为前面的结果是两个Q15格式的运算，结果是Q30格式，需要重新转换为Q15格式
	
	/* Check saturation of Iq */
	if ( wqd_tmp > INT16_MAX )
	{
		hqd_tmp = INT16_MAX;
	}
	else if ( wqd_tmp < ( -32768 ) )
	{
		hqd_tmp = ( -32768 );
	}
	else
	{
		hqd_tmp = ( int16_t )( wqd_tmp );
	}

	output.q = hqd_tmp;

	if ( output.q == ( int16_t )( -32768 ) )
	{
		output.q = -32767;
	}

	/*No overflow guaranteed*/
	d_tmp_1 = input.alpha * ( int32_t )local_vector_components.h_sin;

	/*No overflow guaranteed*/
	d_tmp_2 = input.beta * ( int32_t )local_vector_components.h_cos;

	wqd_tmp = ( d_tmp_1 + d_tmp_2 ) >> 15;

	/* Check saturation of Id */
	if ( wqd_tmp > INT16_MAX )
	{
		hqd_tmp = INT16_MAX;
	}
	else if ( wqd_tmp < ( -32768 ) )
	{
		hqd_tmp = ( -32768 );
	}
	else
	{
		hqd_tmp = ( int16_t )( wqd_tmp );
	}

	output.d = hqd_tmp;

	if ( output.d == ( int16_t )( -32768 ) )
	{
		output.d = -32767;
	}

	return (output);
}
	
/**
  * @brief 反park变换:将同步旋转坐标系下的vqd，变换为静止坐标系的v_alpha,v_beta
  * @param volt_input: vqd
  * @param theta: 电角度值
  */
alphabeta_t mc_rev_park(qd_t volt_input, int16_t theta)
{
	int32_t q_v_alpha_tmp1, q_v_alpha_tmp2, q_v_beta_tmp1, q_v_beta_tmp2;
	trig_components local_vector_components;
	alphabeta_t volt_output;
	
	local_vector_components = mc_trig_functions(theta);

	q_v_alpha_tmp1 = volt_input.q * ( int32_t )local_vector_components.h_cos;
	q_v_alpha_tmp2 = volt_input.d * ( int32_t )local_vector_components.h_sin;
	
	volt_output.alpha = ( int16_t )( ( ( q_v_alpha_tmp1 ) + ( q_v_alpha_tmp2 ) ) >> 15 );
	

	q_v_beta_tmp1 = volt_input.q * ( int32_t )local_vector_components.h_sin;
	q_v_beta_tmp2 = volt_input.d * ( int32_t )local_vector_components.h_cos;
	
	volt_output.beta = ( int16_t )( ( q_v_beta_tmp2 - q_v_beta_tmp1 ) >> 15 );
	
	return (volt_output);
}