CRF详解（理论推导）

本篇是CRF的理论篇，对应的代码解读篇请戳crf++代码解读

基本定义

条件随机场定义

X,Y为随机变量，若Y构成一个由无向图G表示的马尔可夫随机场，即满足：$$P(Y_v|X,Y_w,w\ne v)=P\{Y_v|X,Y_w,w\in N(v)\}$$ 其中$N(v)$表示与点$v$直接相连的点的集合，则称条件概率分布$P(Y|X)$为条件随机场

而马尔可夫随机场满足一条很重要的定理：

Hammersley Clifford定理
一个无向图G是马尔可夫随机场，当且仅当其上的联合概率分布$P(Y)$可以写成G上所有最大团上的势函数的因式分解：$$P(Y)=\frac{1}{Z}\prod _C{\Psi }_C(Y_C)$$
其中规范化因子$Z={\sum }_Y{\prod }_Y{\Psi }_C(Y_C)$，势函数${\Psi }_C(Y_C)$是C上定义的严格正函数

定理的严格证明可参考https://en.wikipedia.org/wiki/Hammersley%E2%80%93Clifford_theorem

---

线性链条件随机场

由于实际应用当中的很多问题都是序列问题，所以我们可以将条件随机场进一步缩小到线性链条件随机场：

设$X=(X_1,...,X_n)和Y=(Y_1,...,Y_n)$均为线性链随机序列，若在给定X的条件下，$P(X|Y)$构成条件随机场，即满足马尔可夫性：$$P(Y_i|X,Y)=P(Y_i|X,Y_{i-1},Y_{i+1}),i=1,2,...,n$$则称$P(Y|X)$为线性链条件随机场

由上述Hammersley Clifford定理，可以给出线性链条件随机场$P(X|Y)$的因式分解式，由于是X和Y都是线性链，因此由Y构成的无向图G上的所有最大团为：$$(Y_1,Y_2),(Y_2,Y_3),...,(Y_{n-1},Y_n)$$
同时又要求${\Psi }_C(Y_C)$严格正，根据 最大熵原则，我们把${\Psi }_{C_i}(Y_{C_i})$定义为指数形式：${\Psi }_{C_i}(Y_{C_i})={\Psi }_i(Y_{i-1},Y_i,X)=exp[{\sum }_h{b}_h(Y_{i-1},Y_i,X,i)+{\sum }_l{u}_l(Y_i,X,i)]$
$$\begin{array}{rl}⟹P(Y|X)& =\frac{1}{Z}\prod _i{\Psi }_i(Y_{i-1},Y_i,X)\\ & =\frac{1}{Z}\prod _{i}exp[\sum _h{b}_h(Y_{i-1},Y_i,X,i)+\sum _l{u}_l(Y_i,X,i)]\\ & =\frac{1}{Z}exp[\sum _{h,i}{b}_h(Y_{i-1},Y_i,X,i)+\sum _{l,i}{u}_l(Y_i,X,i)]\end{array}\text{\hspace{1em}(1.1)}$$
其中$b_k和u_l$称为特征函数，$Z$同样是规范化因子。但在实际使用中，为了方便，通常将$b_k(Y_{i-1},Y_i,X,i)$和$u_l(Y_i,X,i)$定义为0-1函数（人工定义是0还是1），而将不同特征的权重单独记为${\lambda }_k$和${\mu }_l$，因此给定特征函数，特征的权重${\lambda }_k和{\mu }_l$就是线性链CRF的参数。我们可以将上式重新表示为：$$P(Y|X)=\frac{1}{Z}exp[\sum _{h,i}{\lambda }_h{b}_h(Y_{i-1},Y_i,X,i)+\sum _{l,i}{\mu }_l{u}_l(Y_i,X,i)]$$

将符号重新记作：
$$f_k(Y_{i-1},Y_i,X,i)=\{\begin{array}{ll}{b}_h(Y_{i-1},Y_i,X,i)& k=1,..,H\\ u_l(Y_i,X,i)& k=H+1,...,H+L\end{array}\text{\hspace{1em}(1.2)}$$

$$f_k(X,Y)=\sum _{i=1}^n{f}_k(Y_{i-1},Y_i,X,i),f(X,Y)=\sum _{k=1}^K{f}_k(X,Y)\text{\hspace{1em}(1.3)}$$

$$w_k=\{\begin{array}{ll}{\lambda }_h& k=1,..,H\\ {\mu }_l& k=H+1,...,H+L\end{array}\text{\hspace{1em}(1.4)}$$

那么目标函数可以表示为：
$$P(Y|X)=\frac{exp({\sum }_{k=1}^K{w}_k{f}_k(X,Y))}{{\sum }_{Y^{\prime }}exp({\sum }_{k=1}^K{w}_k{f}_k(X,Y^{\prime }))}\text{\hspace{1em}(1.5)}$$

---

特征函数的定义

以CRF++为例，它提供了两种特征模版的形式Unigram和Bigram以供使用者定义自己想用的特征函数。

北 N B
京 N E
欢 V B
迎 V M
你 N E

假如这是我们的数据，第一列的观测序列，第二列是与观测序列相关的feature，在这个数据中是词性，而最后一列需要放状态序列，这个数据里是分词的结果。

特征模板

1.Unigram模版

对应unigram特征函数$u_l(Y_i,X,i)$。形式：%x[row,col]，表示当前位置行数移动row，列数移动col的位置对当前位置output的影响。假设当前位置是"欢 V B"，那么%x[-1,1]就表示当前位置上一个位置的第一个feature，也就是"N"，对当前位置output的影响。再例如U01:%x[0,0]，表示当前位置的观测序列对output的影响，假设状态序列有M种可能的标签，而观测序列的vocabulary数为V，那么U01:%x[0,0]，可以生成$M\times V$个模版，这个例子中M=3，V=5，所以U01:%x[0,0]可以生成如下15个模版：

func1 = if(output = B & feature=U01:“北”) return 1 else return 0
func2 = if(output = M & feature=U01:“北”) return 1 else return 0
func3 = if(output = E & feature=U01:“北”) return 1 else return 0
func4 = if(output = B & feature=U01:“京”) return 1 else return 0
…
func13 = if(output = B & feature=U01:“你”) return 1 else return 0
func14 = if(output = M & feature=U01:“你”) return 1 else return 0
func15 = if(output = E & feature=U01:“你”) return 1 else return 0

从这里也可以看出线性链CRF中$Y_i$对X的依赖是全局的，而不是像HMM一样仅依赖于当前位置。
另：Unigram模版也可以定义为U02:%x[0,0]:%x[1,0]，这表示当前位置的output同时依赖当前位置和下一位置的观测值。

2.Bigram模版
对应bigram特征函数$b_h(Y_{i-1},Y_i,X,i)。$B01%x[0,0]表示当前位置观测序列以及上一位置output对当前位置ouput的影响，例如：

func1 = if(prev_output = B & output = B & feature=B01:“北”) return 1 else return 0
func1 = if(prev_output = M & output = B & feature=B01:“北”) return 1 else return 0
func1 = if(prev_output = E & output = B & feature=B01:“北”) return 1 else return 0
func1 = if(prev_output = B & output = M & feature=B01:“北”) return 1 else return 0
…

而这样的模版总共可以生成$M\times M\times V$个bigram特征函数。从这里也可以看出，如果想增加trigram甚至更高阶的特征函数，那么模型的参数也会程指数级上涨（当然更高阶的特征函数已经不符合CRF的定义范围了）

另：如果只定义为"B"，则表示只考虑prev_output和output，而不考虑观测序列。

---

HMM,MEMM,CRF的比较

1. HMM：
   $\underset{w}{\mathrm{argmax}}P(X,Y;w)=\underset{w}{\mathrm{argmax}}{\prod }_{i=1}^{n}P(y_i|y_{i-1};w)P(x_i|y_i;w)$

2. MEMM: $$\begin{array}{rl}\underset{w}{\mathrm{argmax}}P(Y|X)=& \underset{w}{\mathrm{argmax}}\prod _{i=1}^{n}P(y_i|y_{i-1},X;w)\\ \stackrel{\text{最大熵分类器}}{=}& \underset{w}{\mathrm{argmax}}\prod _{i=1}^n\frac{exp({\sum }_k{w}_k{f}_k(y_{i-1},y_i,X))}{Z_i}\end{array}$$
   其中$Z_i={\sum }_{y^{\prime }}exp({\sum }_k{w}_k{f}_k(y_{i-1}^{\prime },y_i^{\prime },X))$

3. CRF:
   $$\begin{array}{rl}\underset{w}{\mathrm{argmax}}P(Y|X)& =\underset{w}{\mathrm{argmax}}\frac{{\prod }_i{\Psi }_i(Y_{i-1},Y_i,X;w)}{Z}\\ & =\underset{w}{\mathrm{argmax}}\frac{exp({\sum }_k{\sum }_{i=1}^n{w}_k{f}_k(y_{i-1},y_i,X))}{{\sum }_{y^{\prime }}exp({\sum }_k{\sum }_{i=1}^n{w}_k{f}_k(y_{i-1}^{\prime },y_i^{\prime },X))}\end{array}$$

1.HMM和MEMM是有向图，其定义的转移概率是条件概率；CRF是无向图，定义的bigram特征是联合概率。

2.HMM是生成模型，除了用于序列标注，还可以用于数据生成等任务，但缺点是只能利用数据的统计信息，因此需要足够多的数据以保证采样到了数据的全貌；MEMM和CRF是判别模式，旨在找到类别的边界，而且与HMM不同，它们可以直接定义特征，并通过特征捕捉一些仅通过统计数据难以得到的信息，例如字母大小写，词尾信息等。

3.HMM中的观测序列是依赖于状态序列的，而MEMM和CRF中是状态序列依赖于观测序列。前者会导致$P(Y|X)$是无法直接度量的，必须通过贝叶斯法则$P(Y|X)=\frac{P(X,Y)}{P(X)}$来计算,这也解释了为什么HMM是生成模型，而且由于HMM中的未知量是状态向量，刚好契合了EM算法中隐变量的定义，因此还可以使用EM算法做无监督学习（不过无监督的效果会比有监督差很多，所以实践当中大部分还是用有监督方法，并且HMM的有监督方法非常简便，直接通过最大似然估计用频数求解即可）；而后两者则可以直接求解$P(Y|X)$。

4.在HMM中。当前状态$y_i$仅与上一时刻状态$y_{i-1}$和当前观测$x_i$相关，而MEMM和CRF中它是与整个观测序列$X$相关，可以定义$y_i$和观测序列$X$任意位置的关系。

5.MEMM是在将条件概率$P(Y|X)$分解之后再套用的最大熵模型，因此$\underset{w}{\mathrm{argmax}}{\prod }_{i=1}^n\frac{exp({\sum }_k{w}_k{f}_k(y_{i-1},y_i,X))}{Z_i}\rightleftharpoons \underset{w_k}{\mathrm{argmax}}\frac{exp({\sum }_k{w}_k{f}_k(y_{i-1},y_i,X))}{Z_i},\forall k$。也就是最大化每一个位置的条件概率，但这会导致局部最优化问题。而CRF中的归一化因子$Z$是针对整个序列的，它的优化目标是全局最优。

6.由于线性链CRF是马尔可夫随机场，由Hammersley Clifford定理可得，它的最大团只能是相邻的状态，因此线性链CRF只能捕捉到相邻状态之间的特征；而MEMM实际上可以不受这个限制，例如三元组MEMM中，$P(Y|X)={\prod }_{i}P(y_i|y_{i-2},y_{i-1},X)$（参考http://www.cs.columbia.edu/~mcollins/fall2014-loglineartaggers.pdf）

---

学习算法

与HMM类似，CRF的loss function也是根据最大似然估计来定义的:
$$\begin{array}{rl}& \underset{w}{\mathrm{argmin}}-L(w)\\ & =\underset{w}{\mathrm{argmin}}-logP(X,Y)\\ & =\underset{w}{\mathrm{argmin}}-logP(Y|X)P(X)\\ & =\underset{w}{\mathrm{argmin}}-log(\frac{exp({\sum }_{k=1}^K{w}_k{f}_k(X,Y))}{{\sum }_{Y^{\prime }}exp({\sum }_{k=1}^K{w}_k{f}_k(X,Y^{\prime }))})\\ & =\underset{w}{\mathrm{argmin}}-\{\sum _{k=1}^K{w}_k{f}_k(X,Y)-log{Z}_w\}\end{array}\text{\hspace{1em}(3.1)}$$
对$w_k$求导：
$$\begin{array}{rl}\frac{\partial L}{\partial w_k}& =-f_k(Y,X)+\frac{{\sum }_{Y^{\prime }}exp({\sum }_{k=1}^K)f_k(X,Y^{\prime })\ast f_k(X,Y)}{{\sum }_{Y^{\prime }}exp({\sum }_{k=1}^K)f_k(X,Y^{\prime })}\\ & =-f_k(Y,X)+\sum _{Y^{\prime }}P(Y^{\prime }|X)f_k(X,Y)\\ & =-f_k(Y,X)+\sum _{Y^{\prime }}P(Y^{\prime }|X)\sum _{i=1}^n{f}_k(Y_{i-1},Y_i,X,i)\\ & =-f_k(Y,X)+\sum _{i=1}^n\sum _{Y^{\prime }}P(Y^{\prime }|X)f_k(Y_{i-1},Y_i,X,i)\\ & =E_{P(Y^{\prime }|X)}[f_k(Y_{i-1},Y_i,X,i)]-f_k(Y,X)\end{array}\text{\hspace{1em}(3.2)}$$

而后面这一项如果直接计算的话，由于${\sum }_Y^{\prime }P(Y^{\prime }|X)={\sum }_{y_1,..y_n}P(Y_1=y_1,...,Y_n=y_n|X)$，计算复杂度高达$O(M^n\times n)$，所以我们可以采用利用了动态规划思想的前向-后向算法来减少计算量。首先将上式化简为：
$$\begin{array}{rl}\frac{\partial L}{\partial w_k}& =-f_k(Y,X)+E_{P(Y^{\prime }|X)}[f_k(Y_{i-1},Y_i,X,i)]\\ & =-f_k(Y,X)+\sum _{i=1}^n\sum _{Y^{\prime }}P(Y^{\prime }|X)f_k(Y_{i-1},Y_i,X,i)\\ & =-f_k(Y,X)+\sum _{i=1}^n[\sum _{y_i,y_{i-1}}{f}_k(Y_{i-1}=y_{i-1},Y_i=y_i,X,i)P(Y^{\prime },Y_{i-1}=y_{i-1},Y_i=y_i|X)+\sum _{y_i}{f}_k(Y_i=y_i,X,i)P(Y^{\prime },Y_i=y_i|X)]\end{array}\text{\hspace{1em}(3.3)}$$

下面我们首先介绍前向-后向算法，再用这个算法来计算$P(Y^{\prime },Y_{i-1}=y_{i-1},Y_i=y_i|X)$和$P(Y_i=y_i|X)$。

---

前向算法

定义：${\alpha }_i(y_i|X)=\hat{P}(Y_1,...,Y_{i-1},Y_i=y_i|X)$，其中$\hat{P}$是非规范化概率
初始化：$${\alpha }_0(y_0|X)=\{\begin{array}{cc}1& y_0=start\\ 0& y_0\ne start\end{array}$$
递推：
$$\begin{array}{rl}{\alpha }_i(y_i|X)& =\hat{P}(Y_1,...,Y_{i-1},Y_i=y_i|X)\\ & =[\sum _{y_{i-1}}{\Psi }_i(y_{i-1},y_i,X)[\sum _{y_{i-2}}{\Psi }_{i-1}(y_{i-2},y_{i-1},X)\cdots [\sum _{y_1}{\Psi }_1(y_2,y_1,X){\Psi }_0(y_{start},y_1,X)]]]\\ & =\sum _{y_{i-1}}{\Psi }_i(y_{i-1},y_i,X){\alpha }_{i-1}(y_{i-1}|X)\end{array}\text{\hspace{1em}(3.4)}$$

后向算法

定义：${\beta }_i(y_i|X)=\hat{P}(Y_{i+1},...,Y_n|Y_i=y_i,X)$，其中$\hat{P}$是非规范化概率
初始化：$${\beta }_{n+1}(y_{n+1}|X)=\{\begin{array}{cc}1& y_{n+1}=stop\\ 0& y_{n+1}\ne stop\end{array}$$
递推：
$${\beta }_i(y_i|X)=\hat{P}(Y_{i+1},...,Y_n|Y_i=y_i,X)=[\sum _{y_{i+1}}{\Psi }_{i+1}(y_i,y_{i+1},X)[\sum _{y_{i+2}}{\Psi }_{i+2}(y_{i+1},y_{i+2},X)\cdots [\sum _{y_n}{\Psi }_n(y_{n-1},y_n,X){\Psi }_{n+1}(y_n,y_{stop},X)]]]$$
$$⟹\sum _{y_i}{\Psi }_i(y_{i-1},y_i,X){\beta }_i(y_i|X)={\beta }_{i-1}(y_{i-1}|X)\text{\hspace{1em}(3.5)}$$

现在可以计算：
$$Z_w={\alpha }_n^T(X)\cdot 1=1^T\cdot {\beta }_1(X)\text{\hspace{1em}(3.6)}$$

$$\begin{array}{rl}P(Y,Y_i=y_i|X)& =P(Y_1,...,Y_{i-1},Y_i=y_i,Y_{i+1},...,Y_n|X)\\ & =P(Y_1,...,Y_{i-1},Y_i=y_i|X)P(Y_{i+1},...,Y_n|Y_i=y_i,X)\\ & =\frac{{\alpha }_i^T(y_i|X){\beta }_i(y_i|X)}{Z_w}\end{array}\text{\hspace{1em}(3.7)}$$

$$\begin{array}{rl}P(Y,Y_{i-1}=y_{i-1},Y_i=y_i|X)& =P(Y_1,...,Y_{i-2},Y_{i-1}=y_{i-1},Y_i=y_i,...,Y_n|X)\\ & =\frac{1}{Z_w}[\sum _{y_1}{\Psi }_0(y_{start},y_1,X){\Psi }_1(y_2,y_1,X)\cdots \sum _{y_{i-2}}{\Psi }_{i-1}(y_{i-2},y_{i-1},X)\ast \Psi (y_{i-1},y_i,X)\ast \sum _{y_{i+1}}{\Psi }_{i+1}(y_i,y_{i+1},X)\cdots \sum _{y_n}{\Psi }_n(y_{n-1},y_n,X){\Psi }_{n+1}(y_n,y_{stop},X)]\\ & =\frac{{\alpha }_{i-1}(y_{i-1}|X)\Psi (y_{i-1},y_i,X){\beta }_i(y_i|X)}{Z_w}\end{array}\text{\hspace{1em}(3.8)}$$

前面说到直接计算${\sum }_Y^{\prime }P(Y^{\prime }|X)$的计算复杂度是$O(M^n\times n)$，而我们前向-后向算法的计算复杂度仅为$O(M^2\times n)$，所以最终计算${\sum }_Y^{\prime }P(Y^{\prime }|X)$的计算复杂度为$O(M^3\times n)$。

---

正则化

前面有介绍到CRF的参数其实是非常多的，但其中并不是所有的特征函数都对最终的预测结果有重要影响。因此我们需要给目标函数加上正则化项来防止过拟合。常用的正则化项有：
L1正则化: ${\sum }_{k=1}^K|w_k|$，和L2正则化: ${\sum }_{k=1}^K{w}_k^2$。

L1，L2以及Elastic-Net

L1范数其实是L0范数的最优凸近似，因此它倾向于得到更稀疏的结果，即使得很多参数的值为0，所以也可以认为是一种特征筛选。

L2范数的特性会使得它对于大的数值更敏感，因此模型倾向于得到很多值很小的参数（但是不容易为0，而L1范数会直接使得参数为0）；而且由于L2范数是强凸函数，它可以改善目标函数的条件数，增大其凸性，使得求解过程更稳定。

另，参考https://blog.csdn.net/u010725283/article/details/79212762 可知，如果把L2正则项的系数控制在一个合理的范围，那么L2对不同参数的削减由损失函数在这个方向上的凸性强弱决定的：凸性越强，对这个方向上的参数的削减越弱；凸性越弱，则对这个方向上的参数削减越强。

而CRF既可以选择L1正则化，也可以选择L2正则化。为了同时使用两种范数的优点（L1的稀疏性，L2的稳定性）我们可以选择Elastic-Net Penalty：

$$\begin{array}{r}E(w)=L(w)+{\rho }_1\sum _{k=1}^K|w_k|+{\rho }_2\sum _{k=1}^K{w}_k^2\end{array}$$

尽管$E(w)$是凸函数，但是因为它的解析解无法计算，因此我们需要使用优化方法来求解这个问题。

---

优化算法

1.梯度下降法（一阶算法）
2.BFGS（二阶算法）
BFGS详见BFGS

（用BFGS优化CRF模型）

1. 初始化$w_0$，取$B_0=I$，给定特征函数$\{f_k(Y_{i-1},Y_i,X,i){\}}_{k=1}^K,\forall i=1,...,n$
2. 对第k步迭代，$g_k由公式(3.3)求得$。其中$P(Y^{\prime },Y_{i-1}=y_{i-1},Y_i=y_i|X)$和$P(Y^{\prime },Y_i=y_i|X)$由前向-后向算法得到
3. 搜索方向$d_k=-B_k^{-1}{g}_k$
4. 搜索步长${\lambda }_k=argmi{n}_{\lambda }f(w_k+{\lambda }_k{d}_k)$
5. 记${\delta }_k={\lambda }_k{d}_k$， 则有 $w_{k+1}=w_k+{\lambda }_k{d}_k$
6. 再利用前向-后向算法计算$g_{k+1}$，如果$||g_{k+1}||<ϵ$，则停止计算。否则 $B_{k+1}=B_k+\frac{y_k{y}_k^T}{y_k^T{s}_k}-\frac{B_k{s}_k{s}_k^T{B}_k}{s_k^T{B}_k{s}_k}$
7. $k=k+1$,转（3）

---

预测算法

CRF的预测算法与HMM一样，都是采用了利用动态规划思想的Viterbi算法。
由于$$\begin{array}{rl}{y}^{\ast }& =argma{x}_{y}P(Y=y|X=x)\\ & =argma{x}_y\frac{exp(w\ast F(x,y))}{Z(x)}\\ & =argma{x}_y\sum _{i=1}^{n}w\ast F_i(y_{i-1},y_i,x)\end{array}$$
其中$F(x,y)=[f_1(x,y),\cdots ,f_K(x,y){]}^T$，
$F_i(y_{i-1},y_i,x)=[f_1(y_{i-1},y_i,x),\cdots ,f_K(y_{i-1},y_i,x){]}^T$。
因此目标变为寻找使得${\sum }_{i=1}^{n}w\ast F_i(y_{i-1},y_i,x)$最大的路径。HMM中使用Viterbi算法的思想参见 https://zhuanlan.zhihu.com/p/148526621。下面我们直接给出CRF中Viterbi算法的公式：

定义： $${\delta }_i(l)=ma{x}_{y_1,...,y_{i-1}}P(Y_i=l,Y_1,...,Y_{i-1}|X)\text{\hspace{1em}(4.1)}$$
即${\delta }_i(l)$是到节点$(x_i,y_i=l)$的最佳路径的score
初始化： $${\delta }_1(l)=w\ast F_1(y_0=start,y_1=l,x)$$
递推式: $${\delta }_{i+1}(l)=ma{x}_j\{{\delta }_i(j)+w\ast F_{i+1}(Y_i=j,Y_{i+1}=l,X)\}\text{\hspace{1em}(4.2)}$$

另，每一步计算完${\delta }_{i+1}$，要保存$Y_1\to Y_{i+1}$且$Y_{i+1}=j$的最优路径里，$Y_i$的取值：${\psi }_{i+1}(j)=argma{x}_j\{{\delta }_i(j)+w\ast F_{i+1}(Y_i=j,Y_{i+1}=l,X)\}$

---

Viterbi与Beam Search

Viterbi和Beam Search都是序列标注中，用于求最优序列的解码方法。而对于一个长度为$T$，可能的标签数为$N$的序列来说，直接求解最优序列是一个在$N^T$空间上的搜索问题。

• Viterbi: 通过动态规划的方法，去除重复计算，将计算复杂度降到了$O(N^2\times T)$
• Beam Search: 由于Beam Search常用于机器翻译，对话生成等任务上。标签数$N$相当于动辄几万甚至十几万的词典/字典大小，因此即使是$O(N^2\times T)$的计算复杂度也是难以接受的。所以它直接放弃了求解全局最优解，通过在每一步都将候选序列限制在概率最高的top k个，找到一个局部最优解，其计算复杂度为$O(k\times N\times T)$

---

CRF与NN模型的拼接

以NER为例，不管是单独的CRF或者是单独的NN模型（例如LSTM，BiLSTM，Bert等）其实都是可以直接用来做NER的，那为什么要将两个拼接起来呢？这样做的好处是什么？

首先说NN模型，尽管LSTM已经可以考虑到不同时刻对某一位置输出的影响了，但output端始终只能看到input的内容，而看不到output端前后的输出，但在NER任务里，这种前后位置的输出对于判断当前位置的输出是很有帮助的。例如，用NN模型做分词可能出现$<E><B>$这种结果，但是实际上这样的结果是不可能正确的。而CRF恰恰可以解决这样的问题，因此在LSTM后接一个CRF模型，可以通过利用output端前后位置的输出，帮助提高模型的准确度

然后对于CRF模型，由于CRF模型对于人工特征的依赖性比较强（这一点从前面介绍CRF++中的特征函数就可以发现），没有被人工定义的特征是无论如何也学习不到的；而且如果定义太多的特征，又会导致参数空间太大，降低训练效率。而例如BiLSTM/Bert这样的模型刚好可以弥补这个缺陷，利用NN模型的输出来充当CRF的输入，使得可以免于定义人工特征，让模型自然的去学习数据里的统计特征

下面一个问题是NN模型是如何与CRF拼接的：

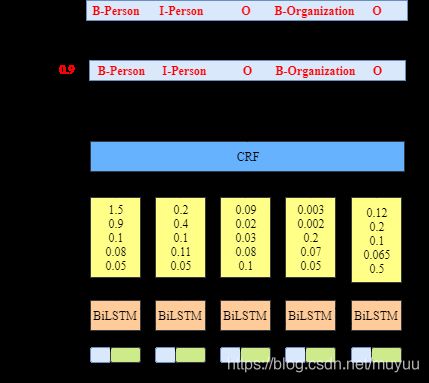
如上图所示BiLSTM会在每个位置都输出一个长度为M的向量，其中M为输出序列tag的数量。而这些向量会作为CRF的unigram特征输入CRF，而这也刚好符合CRF的定义，因为unigram特征定义的就是观测序列X（input）和当前位置状态$Y_i$（output）的关系。而bigram的参数的训练过程与原始CRF一致，会随着整个NN-CRF的迭代而更新。

参见NN+CRF代码https://pytorch.org/tutorials/beginner/nlp/advanced_tutorial.html,可知：1，每一轮迭代是NN和CRF都要训练一遍，即是端到端的训练。2，NN输出的unigram特征进入CRF之后是固定的，CRF训练时只改变bigram的值。3，做inference时，一个query输入进去，也是先经过NN，再经过CRF，因此不同query在进入CRF时的bigram特征是相同的，但unigram的特征会不同（因为不同query用NN做inference的结果不同）