基于改进的混沌引力常数的引力搜索算法（Matlab代码实现）

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 Matlab代码实现

4 参考文献

---

1 概述

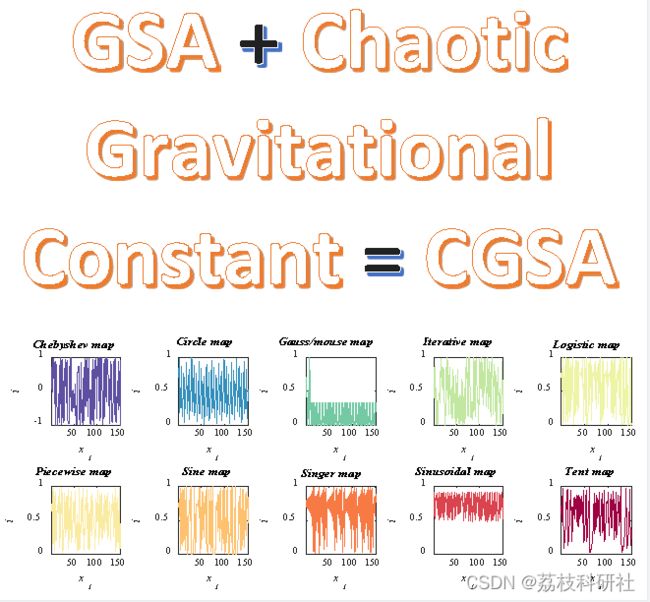
本文将十张混沌图嵌入到最近提出的基于人口的元启发式算法（G）的引力常数（G）中，称为引力搜索算法（GSA）。同时，提出了一种从勘探阶段顺利过渡到开采阶段的自适应归一化方法。作为案例研究，12个偏移和偏置基准函数评估了所提出的基于混沌的GSA算法在探索和开发方面的性能。

在基于群体的元启发式中，搜索过程分为两个主要阶段：探索与开发。在探索阶段，随机行为可以探索尽可能广泛的搜索空间。相比之下，快速开发有前途的地区是后一阶段的主要目标。由于基于群体的元启发式算法的随机性，在这两个阶段之间找到适当的平衡确实具有挑战性。文献表明，混沌地图能够改善这两个阶段。这项工作将十张混沌图嵌入到最近提出的基于人口的元启发式算法（G）的引力常数（G）中，称为引力搜索算法（GSA）。同时，提出了一种从勘探阶段顺利过渡到开采阶段的自适应归一化方法。作为案例研究，12个偏移和偏置基准函数评估了所提出的基于混沌的GSA算法在探索和开发方面的性能。进行称为Wilcoxon秩和的统计检验来判断结果的重要性。结果表明，正弦图是显著提高GSA性能的最佳图谱。

参考文献：

下载链接：Chaotic gravitational constants for the gravitational search algorithm - ScienceDirect 

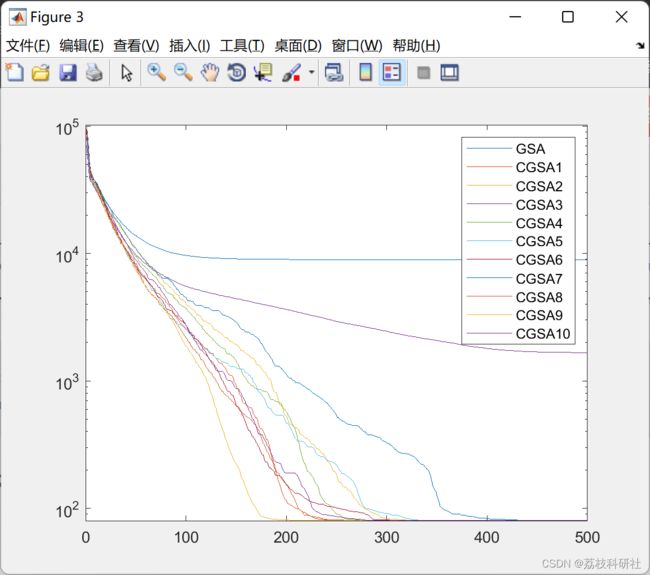
2 运行结果

 部分代码：

clear all

P_no=30;
Max_iteration=500;
Run_no=2;

ElitistCheck=1;

All_Convergence_curves=zeros(2,Max_iteration);

chValue=20;
F_index = 1;

for Algorithm_num=1:11
    for i=1:Run_no
        if Algorithm_num==1
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==2
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==3
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==4
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==5
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==6
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==7
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==8
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==9
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==10
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        if Algorithm_num==11
            cg_curve=GSA(F_index,P_no,Max_iteration,ElitistCheck,Algorithm_num,chValue);
        end
        
        temp(i,:)=cg_curve;
    end
    All_Convergence_curves(Algorithm_num,:)=mean(temp);
end

figure

for k = 1:size(All_Convergence_curves,1)
    
    semilogy(All_Convergence_curves(k,:))
    hold on
end

legend('GSA', 'CGSA1', 'CGSA2', 'CGSA3', 'CGSA4', 'CGSA5', 'CGSA6', 'CGSA7', 'CGSA8', 'CGSA9', 'CGSA10')

save resuls
 

3 Matlab代码实现

4 参考文献

部分理论来源于网络，如有侵权请联系删除。