反向传播算法及其实现

—背景

去年看了《神经网络与深度学习》的前几章，了解了反向传播算法的一些皮毛，当时想自己实现一下，但是由于事情多，就放下了。现在有时间，也是由于想理清这算法就动手推公式和写代码了。

------这里只以全连接层作为例子，主要是我最近的一些理解------

—定义全连接网络

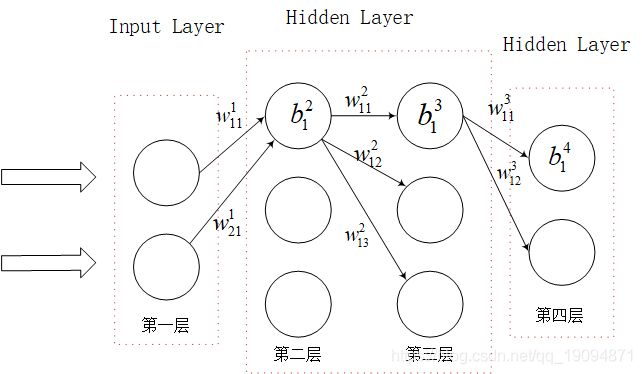
上图所示，说明一下参数：
$w_{ij}^l$：表示第$l$层中的第$i$个神经元与第$l+1$层中第$j$个神经元的权重
$b_i^l$：表示第$l$层中的第$i$个神经元的偏向值
$z_i^l$：表示第$l$层中的第$i$个神经元的输入值，它由前一层对应权重与偏向和。
$a_i^l$：表示第$l$层中的第$i$个神经元的输出值，它是输入值经激活函数计算所得。
这里每个神经元所用激活函数为$sigmoid$函数 $s(x)=\frac{1}{1+e^{-x}}$，顺便算下$s(x)$对$x$求导的结果为：$s^{\prime }(x)=\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}=s(x)(1-s(x))$。
这个网络输出是两个值，可以代表一个二分类网络每个类别的概率。输入是两个值，可以想象每一个样本有两个特征值。

接下来我们举个例子，看网络的前向运算。

—前向运算

输入一个样本$X$，它有两个特征值如下表示：
$$\begin{array}{r}X=\{x_1,x_2\}\end{array}$$
两个特征值进入输入层，也就是第一层的输出值，于是可以依次计算出第二层每个神经元的输入值和激活值（对下一层的输出值）：

$z_1^2=w_{11}^1\cdot x_1+w_{21}^1\cdot x_2+b_1^2$

$z_2^2=w_{12}^1\cdot x_1+w_{22}^1\cdot x_2+b_2^2$

$z_3^2=w_{13}^1\cdot x_1+w_{23}^1\cdot x_2+b_3^2$

$a_1^2=s(z_1^2)$

$a_2^2=s(z_2^2)$

$a_3^2=s(z_3^2)$

接下来算出第三层每个神经元的输入值和对下一层的输出值：

$z_1^3=w_{11}^2\cdot a_1^2+w_{21}^2\cdot a_2^2+w_{31}^2\cdot a_3^2+b_1^3$

$z_2^3=w_{12}^2\cdot a_1^2+w_{22}^2\cdot a_2^2+w_{32}^2\cdot a_3^2+b_2^3$

$z_3^3=w_{13}^2\cdot a_1^2+w_{23}^2\cdot a_2^2+w_{33}^2\cdot a_3^2+b_3^3$

$a_1^3=s(z_1^3)$

$a_2^3=s(z_2^3)$

$a_3^3=s(z_3^3)$

有了第三层激活值，那么可以算出第四层，也就是输出层的值：

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

$z_2^4=w_{12}^3\cdot a_1^3+w_{22}^3\cdot a_2^3+w_{32}^3\cdot a_3^3+b_2^4$

$a_1^4=s(z_1^4)$

$a_2^4=s(z_2^4)$

得到网络的输出值$a_1^4,a_2^4$，我们与真实值相比较，设对于样本$X$的标签为$Y=\{y_1,y_2\}$。那么算出网络计算值与真实值的差距$loss$,这里用平方差：
$$\begin{array}{r}loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}\end{array}$$
有了损失值，那么，我们应该优化网络参数，不断降低损失值。这里采用最常用的梯度下降法，来求loss的最小值。因为，沿梯度相反的方向，就是函数值下降最快的方向。那么接下来就是求每个$l$关于$w,b$的梯度，然后按照一定的学习率$lr$更新这些参数，如下：
$$\begin{array}{r}w=w-lr\cdot \frac{\mathfrak{d}loss}{\mathfrak{d}w}（1）\end{array}$$
$$\begin{array}{r}b=b-lr\cdot \frac{\mathfrak{d}loss}{\mathfrak{d}b}（2）\end{array}$$
，总有一天，loss会降到最低，令我们满意。
那么，计算每个$w,b$的梯度，这和前向计算一样，是一件体力活，接下来就采用链式求导来依次计算出$\frac{\mathfrak{d}loss}{\mathfrak{d}w}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}b}$

—链式求导

从最后一层开始，求$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{12}^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{21}^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{22}^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{31}^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{32}^3}$以及$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_1^4}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_2^4}$：

参照上面前向计算式子，从后往前看,直到遇见 $b_1^4$为止：

$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$

$a_1^4=s(z_1^4)$

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

那么可以依照链式求导法则来求 $loss$对$b_1^4$的偏导数：

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_1^4}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_1^4}\cdot \frac{\mathfrak{d}{a}_1^4}{\mathfrak{d}{z}_1^4}\cdot \frac{\mathfrak{d}{z}_1^4}{\mathfrak{d}{b}_1^4}\\ & =-\frac{1}{2}\cdot 2\cdot (y_1-a_1^4)\cdot s(z_1^4)\cdot (1-s(z_1^4))\\ & =-(y_1-a_1^4)\cdot s(z_1^4)\cdot (1-s(z_1^4))\end{array}$

同理可以得到下面：

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_2^4}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_2^4}\cdot \frac{\mathfrak{d}{a}_2^4}{\mathfrak{d}{z}_2^4}\cdot \frac{\mathfrak{d}{z}_2^4}{\mathfrak{d}{b}_2^4}\\ & =-\frac{1}{2}\cdot 2\cdot (y_2-a_2^4)\cdot s(z_2^4)\cdot (1-s(z_2^4))\\ & =-(y_2-a_2^4)\cdot s(z_2^4)\cdot (1-s(z_2^4))\end{array}$

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^3}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_1^4}\cdot \frac{\mathfrak{d}{a}_1^4}{\mathfrak{d}{z}_1^4}\cdot \frac{\mathfrak{d}{z}_1^4}{\mathfrak{d}{w}_{11}^3}\end{array}$

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{12}^3}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_2^4}\cdot \frac{\mathfrak{d}{a}_2^4}{\mathfrak{d}{z}_2^4}\cdot \frac{\mathfrak{d}{z}_2^4}{\mathfrak{d}{w}_{12}^3}\end{array}$
$......$照这样计算下去就可以把这一层参数偏导数全求出来。
最后一层求出之后，再求倒数第二层$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{12}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{13}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{21}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{22}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{23}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{31}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{32}^2}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{33}^2}$以及$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_1^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_2^3}$、$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_2^3}$：

这一层有点深，求$\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_1^3}$，从后往前看：

$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$

$a_1^4=s(z_1^4)$

$a_2^4=s(z_2^4)$

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

$z_2^4=w_{12}^3\cdot a_1^3+w_{22}^3\cdot a_2^3+w_{32}^3\cdot a_3^3+b_2^4$

$a_1^3=s(z_1^3)$

$z_1^3=w_{11}^2\cdot a_1^2+w_{21}^2\cdot a_2^2+w_{31}^2\cdot a_3^2+b_1^3$

直到出现$b_1^3$,然后求偏导数：

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{b}_1^3}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_1^4}\cdot \frac{\mathfrak{d}{a}_1^4}{\mathfrak{d}{z}_1^4}\cdot \frac{\mathfrak{d}{z}_1^4}{\mathfrak{d}{a}_1^3}\cdot \frac{\mathfrak{d}{a}_1^3}{\mathfrak{d}{z}_1^3}\cdot \frac{\mathfrak{d}{z}_1^3}{\mathfrak{d}{b}_1^3}+\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_2^4}\cdot \frac{\mathfrak{d}{a}_2^4}{\mathfrak{d}{z}_2^4}\cdot \frac{\mathfrak{d}{z}_2^4}{\mathfrak{d}{a}_1^3}\cdot \frac{\mathfrak{d}{a}_1^3}{\mathfrak{d}{z}_1^3}\cdot \frac{\mathfrak{d}{z}_1^3}{\mathfrak{d}{b}_1^3}\end{array}$

好了，接下来看$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^2}$：

$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$

$a_1^4=s(z_1^4)$

$a_2^4=s(z_2^4)$

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

$z_2^4=w_{12}^3\cdot a_1^3+w_{22}^3\cdot a_2^3+w_{32}^3\cdot a_3^3+b_2^4$

$a_1^3=s(z_1^3)$

$z_1^3=w_{11}^2\cdot a_1^2+w_{21}^2\cdot a_2^2+w_{31}^2\cdot a_3^2+b_1^3$

看到了$w_{11}^2$,那就求导：

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^2}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_1^4}\cdot \frac{\mathfrak{d}{a}_1^4}{\mathfrak{d}{z}_1^4}\cdot \frac{\mathfrak{d}{z}_1^4}{\mathfrak{d}{a}_1^3}\cdot \frac{\mathfrak{d}{a}_1^3}{\mathfrak{d}{z}_1^3}\cdot \frac{\mathfrak{d}{z}_1^3}{\mathfrak{d}{w}_{11}^2}+\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_2^4}\cdot \frac{\mathfrak{d}{a}_2^4}{\mathfrak{d}{z}_2^4}\cdot \frac{\mathfrak{d}{z}_2^4}{\mathfrak{d}{a}_1^3}\cdot \frac{\mathfrak{d}{a}_1^3}{\mathfrak{d}{z}_1^3}\cdot \frac{\mathfrak{d}{z}_1^3}{\mathfrak{d}{w}_{11}^2}\end{array}$

接下来，算其它的也是一样的方法，这里就不赘述了！
求出所有层的参数，然后按照梯度下降法的公式（1）、（2），更新一次参数。再不断重复这个前向运算和后向求偏导并更新参数过程，使得$loss$降到最低。

这里大家可能就发现问题了，这样求导，越往深处求，越发现，有些偏导数前面的都是一样的，而且已经求过了，在求所有偏导数时，存在大量的不必要的重复计算。那怎么才能优化它呢？接下来就介绍反向传播算法来加速网络求梯度。

—反向传播算法

反向传播算法，我的理解就是引入$\delta$,从后往前计算梯度时，每计算完一个参数梯度，就先保存下来，然后再计算前面梯度时，直接用先前保存下来的梯度值继续计算。这样避免重复计算！

介绍一个符号，当两个矩阵的行和列相同时，运算符$\odot$表示矩阵点乘：

$$\begin{array}{r}\left[\begin{array}{l}1\\ 2\end{array}\right]\odot \left[\begin{array}{l}3\\ 4\end{array}\right]=\left[\begin{array}{l}1\ast 3\\ 2\ast 4\end{array}\right]=\left[\begin{array}{l}3\\ 8\end{array}\right]\end{array}$$

ok，下面讲的是算法思想：

我们先定义${\delta }_i^l$表示第$l$层的第$i$个神经元的对输出结果的误差:

$$\begin{array}{r}{\delta }_i^l=\frac{\mathfrak{d}loss}{\mathfrak{d}{z}_i^l}\end{array}$$

这其实好理解，因为$z_i^l$细微的变化会引起结果发生变化，由于网络都是加和乘运算，所以，$z_i^l$变大，肯定引起$loss$变大。那么，引起这样一个不好的变化就是我们定义的误差。

由于反向传播算法论文里面提到四个重要的公式，我这里先直接写出来，后面理解时，再反复来看这四个公式。公式如下：

• 输出层的误差计算如下：
  $${\delta }_j^L=\frac{\partial loss}{\partial a_j^L}{s}^{\prime }\left(z_j^L\right)$$
  这就是loss对$z_j^L$求导。先对激活值求导，再由激活值对$z_j^L$求导。这里特指在输出层。由于网络都是矩阵运算，我们可以将公式改写成矩阵运算的形式，如下：
  $${\delta }^L={\nabla }_{a}loss\odot s^{\prime }\left(z^L\right)$$
  ${\nabla }_{a}loss$表示$loss$对激活值的偏导数。回头看损失函数$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$，$loss$对$a$求偏导，可以算出为$-(y_i-a_i^4)$,那么把${\nabla }_{a}loss$替换掉，写成：
  $${\delta }^L=\left(a^L-y\right)\odot s^{\prime }\left(z^L\right)$$
• 由输出层的误差，反向计算前面各层每个神经元的误差，式子如下：
  $${\delta }^l=\left({\left(w^l\right)}^T{\delta }^{l+1}\right)\odot s^{\prime }\left(z^l\right)$$
  前面一部分是后面的误差通过权重传递到前面，后面点乘当前神经元的激活对输入偏导是将误差通过激活函数传递到当前神经元。具体做法见下图根据最后一层误差，反向求${\delta }_1^3$：
  
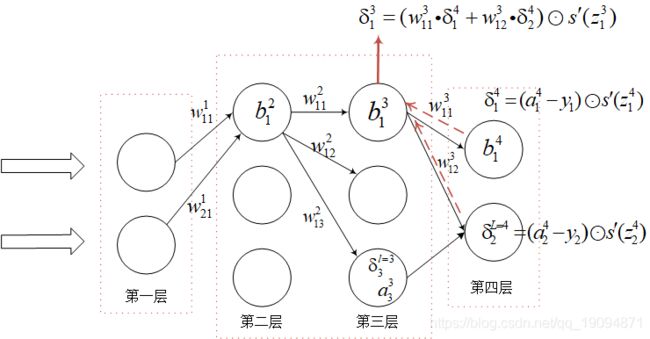
• 有前面两个公式就可以算出所有神经元上的误差，根据这个误差，就可以算出损失函数对偏向的偏导数：
  $$\frac{\partial loss}{\partial b_j^l}={\delta }_j^l$$
• 损失函数对权重的偏导数：
  $$\frac{\partial loss}{\partial w_{ij}^l}=a_i^l{\delta }_j^{l+1}$$
  形象点，看下图红色箭头求损失函数对$w_{32}^3$偏导数：
  
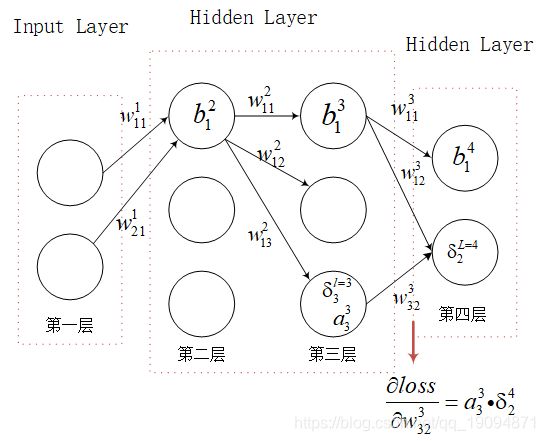
  接下来，讲为什么是这样，其实，很简单，这四个公式都是前面讲的链式法则推导出来的结果。
  带着疑问，我来慢慢解答，并以几个求权重和偏向的偏导数例子来证明上述公式。
  前面链式法则求所有参数偏导数时，存在很多重复计算，那么反向传播算法就来解决这个问题。
  首先，定义输出层误差$\delta$,这是为了方便后续表达。仔细看这个公式：
  $${\delta }^L=\left(a^L-y\right)\odot s^{\prime }\left(z^L\right)$$
  这就是损失函数对最后一层神经单元的$z$求偏导，有了这个公式，我们先用链式法则计算前面层的${\delta }_i^{l=L-1}$：

$$\begin{array}{r}{\delta }_i^l=\frac{\partial loss}{\partial z_i^l}=\frac{\partial loss}{\partial a_1^L}\cdot \frac{\partial a_1^L}{\partial z_1^L}\cdot \frac{\partial z_1^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}+\frac{\partial loss}{\partial a_2^L}\cdot \frac{\partial a_2^L}{\partial z_2^L}\cdot \frac{\partial z_2^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}+...+\frac{\partial loss}{\partial a_n^L}\cdot \frac{\partial a_n^L}{\partial z_n^L}\cdot \frac{\partial z_n^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}\end{array}$$
其中n代表最后一层神经元个数,接下来化简：

$\begin{array}{r}\frac{\partial loss}{\partial a_1^L}\cdot \frac{\partial a_1^L}{\partial z_1^L}={\delta }_1^L...\frac{\partial loss}{\partial a_n^L}\cdot \frac{\partial a_n^L}{\partial z_n^L}={\delta }_n^L\end{array}$

而$\begin{array}{r}\frac{\partial z_1^L}{\partial a_i^{L-1}}=w_{i1}^{L-1}...\frac{\partial z_n^L}{\partial a_i^{L-1}}=w_{in}^{L-1}\end{array}$,这可以从网络中的公式看出来。

那么上面公式可以化简：

$\begin{array}{rl}{\delta }_i^l=\frac{\partial loss}{\partial z_i^l}& =\frac{\partial loss}{\partial a_1^L}\cdot \frac{\partial a_1^L}{\partial z_1^L}\cdot \frac{\partial z_1^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}+\frac{\partial loss}{\partial a_2^L}\cdot \frac{\partial a_2^L}{\partial z_2^L}\cdot \frac{\partial z_2^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}+...+\frac{\partial loss}{\partial a_n^L}\cdot \frac{\partial a_n^L}{\partial z_n^L}\cdot \frac{\partial z_n^L}{\partial a_i^{L-1}}\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}\\ & =({\delta }_1^L\cdot w_{i1}^{L-1}+...+{\delta }_n^L\cdot w_{in}^{L-1})\cdot \frac{\partial a_i^{L-1}}{\partial z_i^{L-1}}\\ & =({\delta }_1^L\cdot w_{i1}^{L-1}+...+{\delta }_n^L\cdot w_{in}^{L-1=l})\odot s^{\prime }(z_i^{L-1=l})\end{array}$

那么这一层就把公式二证明完毕！

接下来，从例子出发，这样会更加清晰，求${\delta }_1^3$:

从后往前找到${\delta }_1^3$为止：

$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$

$a_1^4=s(z_1^4)$

$a_2^4=s(z_2^4)$

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

$z_2^4=w_{12}^3\cdot a_1^3+w_{22}^3\cdot a_2^3+w_{32}^3\cdot a_3^3+b_2^4$

$a_1^3=s(z_1^3)$

$\begin{array}{rl}{\delta }_1^3=\frac{\partial loss}{\partial z_1^3}& =\frac{\partial loss}{\partial a_1^4}\cdot \frac{\partial a_1^4}{\partial z_1^4}\cdot \frac{\partial z_1^4}{\partial a_1^3}\cdot \frac{\partial a_1^3}{\partial z_1^3}+\frac{\partial loss}{\partial a_2^4}\cdot \frac{\partial a_2^4}{\partial z_2^4}\cdot \frac{\partial z_2^4}{\partial a_1^3}\cdot \frac{\partial a_1^3}{\partial z_1^3}\\ & ={\delta }_1^4\cdot w_{11}^3\cdot s^{\prime }(z_1^3)+{\delta }_2^4\cdot w_{12}^3\cdot s^{\prime }(z_1^3)\\ & =({\delta }_1^4\cdot w_{11}^3+{\delta }_2^4\cdot w_{12}^3)\cdot s^{\prime }(z_1^3)\end{array}$

和图中所示计算一样。
接下来证明公式三：
由公式二可以得到每个神经单元的误差$\delta =\frac{\partial loss}{\partial z}$,算$\frac{\partial loss}{\partial w_{ij}^{l=L-1}}$:
$\begin{array}{rl}\frac{\partial loss}{\partial w_{ij}^{l=L-1}}& =\frac{\partial loss}{\partial a_j^L}\cdot \frac{\partial a_j^L}{\partial z_j^L}\cdot \frac{\partial z_j^L}{\partial w_{ij}^{L-1}}\\ & 由于\frac{\partial loss}{\partial a_j^L}\cdot \frac{\partial a_j^L}{\partial z_j^L}={\delta }_j^L，而且根据前向计算公式可以发现：\frac{\partial z_j^L}{\partial w_{ij}^{L-1}}=a_i^{L-1}\\ & 所以原式={\delta }_j^L\cdot a_i^{L-1}\end{array}$
和上图第三个反向传播公式一致。

下面举个例子，更加清晰！求$\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^3}$：

由前向计算式子查看：

$loss=\frac{(y_1-a_1^4{)}^2+(y_2-a_2^4{)}^2}{2}$

$a_1^4=s(z_1^4)$

$z_1^4=w_{11}^3\cdot a_1^3+w_{21}^3\cdot a_2^3+w_{31}^3\cdot a_3^3+b_1^4$

找到$w_{11}^3$,进行如下求导：

$\begin{array}{rl}\frac{\mathfrak{d}loss}{\mathfrak{d}{w}_{11}^3}& =\frac{\mathfrak{d}loss}{\mathfrak{d}{a}_1^4}\cdot \frac{\mathfrak{d}{a}_1^4}{\mathfrak{d}{z}_1^4}\cdot \frac{\mathfrak{d}{z}_1^4}{\mathfrak{d}{w}_{11}^3}\end{array}={\delta }_1^L\cdot a_1^3$

OK,同理也可以推导出对偏向求导，这里就不赘述了。
这只是推导出倒数第二层的四个公式成立，那么同理，再往前推，公式也一样可以推导出来，这里就不干这个体力活了！

那么接下来，就是实现代码：

代码一（较粗糙，代码二会改进），预测sin(x)曲线

# -*- coding: utf-8 -*-
'''
    20191119
    构建简单的全连接神经网络，实现前向计算和反向传播算法求导
'''
import numpy as np
import math
import matplotlib.pyplot as plt
from tqdm import tqdm
class SimpleNerworks:
    '''
    我希望实例化这个类的时候，你就想好了网络的层数，以及每层网络的神经元个数
    传入格式为： {第一层：2个神经元，第二层：3个神经元，第三层：4个神经元，第四层：1个神经元}
    '''
    def __init__(self,*kwargs):
        super(SimpleNerworks, self).__init__()
        assert len(kwargs)>=2
        #初始化权重和偏差
        self.weights = [np.mat(np.random.randn(y,x)) for x,y in zip(kwargs[:-1],kwargs[1:])]
        self.bias = [np.mat(np.random.randn(y,1)) for y in kwargs[1:]]
        self.a = [np.mat(np.zeros((y,1))) for y in kwargs] #每个神经元的输出值，输入层直接是x，其他层则为a = sigmoid(z)
        self.z = [np.mat(np.zeros_like(b)) for b in self.bias] #每个神经元的输入值，输入层就算了，z = wx+b
        self.delta = [np.mat(np.zeros_like(b)) for b in self.bias]

    def forward(self,put:list):
        #前向运算,顺便保存中间参数a,z，方便反向计算梯度
        self.a[0] = np.mat(put)
        for i,w_b in enumerate(zip(self.weights,self.bias)):
            w,b=w_b
            self.z[i]=w.dot(self.a[i]) + b
            self.a[i+1]=self.Sigmoid(self.z[i])
            put = self.a[i+1]
        return self.a[-1]

    def backpropagation(self,y_pre,y_real):
        '''
        反向传播
        计算出每个神经元的delta，按照反向传播公式求出所有梯度
        :return: 返回每个w，b的梯度
        '''

        #先算出最后一层的delta
        self.delta[-1] = np.multiply(np.mat(y_pre - y_real),self.Sigmoid_derivative(self.z[-1]))

        #算出所有delta
        i = len(self.delta) -1
        while i>=1:
            self.delta[i-1] = np.multiply(np.dot(self.weights[i].T,self.delta[i]) , self.Sigmoid_derivative(self.z[i-1]))
            i -= 1

        #利用delta算出所有参数的梯度
        delta_bias = self.delta
        delta_weights = [ D.dot(A.T) for D,A in zip(self.delta,self.a[:-1])]
        return delta_weights,delta_bias

    def updata_w_b(self,delta_weights,delta_bias,lr):
        '''
        :param delta_weights: w的梯度
        :param delta_bias: b的梯度
        :param lr: 学习率
        更新self.weights,self.bias
        '''
        for i in range(len(delta_weights)):
            self.bias[i] = self.bias[i] - lr * delta_bias[i]
            self.weights[i] = self.weights[i] - lr * delta_weights[i]

    def Sigmoid(self,x):
        #sigmoid函数
        s = 1 / (1 + np.exp(-x))
        return s

    def Sigmoid_derivative(self,x):
        # sigmoid函数对x的求导
        return np.multiply(self.Sigmoid(x),1 - self.Sigmoid(x))

    def loss_function(self,y_pre,y_real):
        '''
        :param y_pre: 网络计算值
        :param y_real: 真实值
        :return: 1/2 *(y_pre-y_real)^2
        这里我之所以前面乘以1/2，是因为，这样loss对里面的y_pre求导，刚好等于y_pre-y_real，十分简洁
        '''
        return 0.5*pow(y_pre-y_real,2).sum()

def DataSinX():
    '''
    生成x,sin(x),打乱。
    :return:
    '''
    data = [(i,math.sin(i)) for i in np.arange(-5 * math.pi, 5 * math.pi, 0.1)]
    np.random.shuffle(data)
    return data

def DataIter(Data):
    '''
    :param X: x
    :param Y: sin(x)
    :return:
    '''
    for i in range(len(Data)):
        yield Data[i]

def ShowData(axs,x,y,c,marker,legend):

    axs.scatter(x, y, marker=marker, color=c)
    axs.legend(legend)



if __name__ == '__main__':
    Data = DataSinX()
    DataIter(Data)
    fig, axs = plt.subplots()
    net = SimpleNerworks(1,2,3,2,1)
    for i in tqdm(range(1,100)):
        for x,Y in DataIter(Data):
            y = net.forward([x])
            delta_weights,delta_bias =net.backpropagation(y,Y)
            net.updata_w_b(delta_weights,delta_bias,0.01)
            ShowData(axs=axs, x=x, y=Y, marker='*', c=(0.8, 0., 0.), legend='sinx')
            ShowData(axs=axs, x=x, y=Y, marker='.', c=(0., 0.5, 0.), legend='P')
        print("----loss:{}---".format(net.loss_function(y,Y)))
    fig.show()



    # fig,axs = plt.subplots()
    # for x,y in DataIter(Data):
    #     ShowData(axs=axs,x=x,y=y,marker='*',c=(0.8,0.,0.),legend='sinx')
    #     ShowData(axs=axs, x=x, y=y-1, marker='.', c=(0., 0.5, 0.), legend='learn')
    # fig.show()

结果：

  0%|                                                    | 0/99 [00:00<?, ?it/s]----loss:0.08218073585832743---
  1%|▍                                           | 1/99 [00:03<05:20,  3.27s/it]----loss:0.0798943153067189---
  2%|▉                                           | 2/99 [00:06<05:21,  3.31s/it]----loss:0.07789974959818005---
  3%|█▎                                          | 3/99 [00:10<05:32,  3.46s/it]----loss:0.07614294783023841---
  4%|█▊                                          | 4/99 [00:14<05:42,  3.60s/it]----loss:0.07458248315071356---
  5%|██▏                                         | 5/99 [00:18<05:54,  3.77s/it]----loss:0.07318609280327401---
  6%|██▋                                         | 6/99 [00:23<06:08,  3.96s/it]----loss:0.0719282753431308---
  7%|███                                         | 7/99 [00:27<06:19,  4.12s/it]----loss:0.07078860492973296---
  8%|███▌                                        | 8/99 [00:32<06:36,  4.36s/it]----loss:0.06975052549045974---
  9%|████                                        | 9/99 [00:38<07:13,  4.81s/it]----loss:0.06880047292276117---
 10%|████▎                                      | 10/99 [00:43<07:22,  4.97s/it]----loss:0.06792722589782152---
 11%|████▊                                      | 11/99 [00:49<07:37,  5.20s/it]----loss:0.06712141877667446---
 12%|█████▏                                     | 12/99 [00:55<07:48,  5.39s/it]----loss:0.06637517133179552---
 13%|█████▋                                     | 13/99 [01:01<08:17,  5.79s/it]----loss:0.06568180386305453---
 14%|██████                                     | 14/99 [01:08<08:35,  6.07s/it]----loss:0.06503561558313474---
 15%|██████▌                                    | 15/99 [01:15<08:44,  6.24s/it]----loss:0.06443171045970558---
 16%|██████▉                                    | 16/99 [01:22<08:58,  6.48s/it]----loss:0.06386585906003966---
 17%|███████▍                                   | 17/99 [01:30<09:25,  6.89s/it]----loss:0.06333438799704556---
 18%|███████▊                                   | 18/99 [01:37<09:27,  7.01s/it]----loss:0.06283409074359572---
 19%|████████▎                                  | 19/99 [01:44<09:32,  7.15s/it]----loss:0.062362155140612836---
 20%|████████▋                                  | 20/99 [01:53<10:06,  7.67s/it]----loss:0.06191610405800253---
 21%|█████████                                  | 21/99 [02:04<11:04,  8.53s/it]----loss:0.061493746501050044---
 22%|█████████▌                                 | 22/99 [02:17<12:40,  9.88s/it]----loss:0.06109313707402205---
 23%|█████████▉                                 | 23/99 [02:31<13:57, 11.02s/it]----loss:0.06071254217698073---
 24%|██████████▍                                | 24/99 [02:41<13:40, 10.94s/it]----loss:0.06035041166309115---
 25%|██████████▊                                | 25/99 [02:51<13:07, 10.64s/it]----loss:0.06000535495171597---
 26%|███████████▎                               | 26/99 [03:07<14:38, 12.04s/it]----loss:0.05967612079871905---
 27%|███████████▋                               | 27/99 [03:24<16:16, 13.56s/it]----loss:0.05936158008511355---
 28%|████████████▏                              | 28/99 [03:42<17:46, 15.02s/it]----loss:0.05906071110982107---
 29%|████████████▌                              | 29/99 [03:55<16:49, 14.43s/it]----loss:0.058772586970220066---
 30%|█████████████                              | 30/99 [04:08<16:00, 13.93s/it]----loss:0.05849636469156972---
 31%|█████████████▍                             | 31/99 [04:21<15:30, 13.69s/it]----loss:0.05823127582796268---
 32%|█████████████▉                             | 32/99 [04:35<15:29, 13.87s/it]----loss:0.05797661830671369---
 33%|██████████████▎                            | 33/99 [04:50<15:27, 14.06s/it]----loss:0.05773174932770428---
 34%|██████████████▊                            | 34/99 [05:08<16:44, 15.45s/it]----loss:0.05749607916123627---
 35%|███████████████▏                           | 35/99 [05:31<18:53, 17.71s/it]----loss:0.057269065713969454---
 36%|███████████████▋                           | 36/99 [05:55<20:15, 19.30s/it]----loss:0.05705020975376913---
 37%|████████████████                           | 37/99 [06:17<20:58, 20.30s/it]----loss:0.05683905070171422---
 38%|████████████████▌                          | 38/99 [06:37<20:33, 20.22s/it]----loss:0.05663516291386805---
 39%|████████████████▉                          | 39/99 [06:56<19:43, 19.73s/it]----loss:0.05643815238728767---
 40%|█████████████████▎                         | 40/99 [07:17<19:51, 20.19s/it]----loss:0.05624765383460416---
 41%|█████████████████▊                         | 41/99 [07:41<20:37, 21.34s/it]----loss:0.056063328079724827---
 42%|██████████████████▏                        | 42/99 [08:07<21:41, 22.83s/it]----loss:0.055884859734082706---
 43%|██████████████████▋                        | 43/99 [08:35<22:42, 24.34s/it]----loss:0.055711955118630745---
 44%|███████████████████                        | 44/99 [09:00<22:22, 24.40s/it]----loss:0.055544340401642425---
 45%|███████████████████▌                       | 45/99 [09:23<21:32, 23.93s/it]----loss:0.0553817599264888---
 46%|███████████████████▉                       | 46/99 [09:47<21:15, 24.07s/it]----loss:0.05522397470704746---
 47%|████████████████████▍                      | 47/99 [10:12<21:07, 24.37s/it]----loss:0.055070761071362974---
 48%|████████████████████▊                      | 48/99 [10:38<21:00, 24.72s/it]----loss:0.05492190943670524---
 49%|█████████████████████▎                     | 49/99 [11:05<21:11, 25.44s/it]----loss:0.05477722320133363---
 51%|█████████████████████▋                     | 50/99 [11:31<20:52, 25.55s/it]----loss:0.054636517740130175---
 52%|██████████████████████▏                    | 51/99 [11:58<20:59, 26.25s/it]----loss:0.05449961949285859---
 53%|██████████████████████▌                    | 52/99 [12:24<20:25, 26.07s/it]----loss:0.05436636513518095---
 54%|███████████████████████                    | 53/99 [12:51<20:14, 26.41s/it]----loss:0.05423660082375039---
 55%|███████████████████████▍                   | 54/99 [13:20<20:15, 27.02s/it]----loss:0.054110181507729435---
 56%|███████████████████████▉                   | 55/99 [13:49<20:24, 27.83s/it]----loss:0.05398697029997453---
 57%|████████████████████████▎                  | 56/99 [14:24<21:26, 29.92s/it]----loss:0.05386683790190694---
 58%|████████████████████████▊                  | 57/99 [14:53<20:43, 29.62s/it]----loss:0.05374966207676673---
 59%|█████████████████████████▏                 | 58/99 [15:24<20:29, 29.99s/it]----loss:0.053635327166539785---
 60%|█████████████████████████▋                 | 59/99 [15:56<20:24, 30.60s/it]----loss:0.05352372364836692---
 61%|██████████████████████████                 | 60/99 [16:30<20:36, 31.69s/it]----loss:0.05341474772669764---
 62%|██████████████████████████▍                | 61/99 [17:07<20:59, 33.16s/it]----loss:0.05330830095785497---
 63%|██████████████████████████▉                | 62/99 [17:40<20:22, 33.04s/it]----loss:0.053204289904025925---
 64%|███████████████████████████▎               | 63/99 [18:14<19:59, 33.31s/it]----loss:0.05310262581400647---
 65%|███████████████████████████▊               | 64/99 [18:47<19:31, 33.46s/it]----loss:0.053003224328303296---
 66%|████████████████████████████▏              | 65/99 [19:22<19:10, 33.83s/it]----loss:0.05290600520643899---
 67%|████████████████████████████▋              | 66/99 [20:01<19:29, 35.44s/it]----loss:0.05281089207452103---
 68%|█████████████████████████████              | 67/99 [20:39<19:13, 36.04s/it]----loss:0.05271781219133017---
 69%|█████████████████████████████▌             | 68/99 [21:14<18:31, 35.87s/it]----loss:0.052626696231351106---
 70%|█████████████████████████████▉             | 69/99 [21:53<18:24, 36.83s/it]----loss:0.05253747808332267---
 71%|██████████████████████████████▍            | 70/99 [22:31<17:57, 37.16s/it]----loss:0.05245009466301887---
 72%|██████████████████████████████▊            | 71/99 [23:11<17:43, 37.98s/it]----loss:0.05236448573909454---
 73%|███████████████████████████████▎           | 72/99 [23:50<17:12, 38.25s/it]----loss:0.05228059377093726---
 74%|███████████████████████████████▋           | 73/99 [24:34<17:22, 40.11s/it]----loss:0.05219836375756433---
 75%|████████████████████████████████▏          | 74/99 [25:17<17:01, 40.87s/it]----loss:0.052117743096692135---
 76%|████████████████████████████████▌          | 75/99 [25:59<16:26, 41.11s/it]----loss:0.05203868145318096---
 77%|█████████████████████████████████          | 76/99 [26:43<16:06, 42.02s/it]----loss:0.05196113063613246---
 78%|█████████████████████████████████▍         | 77/99 [27:27<15:41, 42.78s/it]----loss:0.051885044483977925---
 79%|█████████████████████████████████▉         | 78/99 [28:14<15:22, 43.95s/it]----loss:0.05181037875695312---
 80%|██████████████████████████████████▎        | 79/99 [29:00<14:50, 44.51s/it]----loss:0.0517370910364093---
 81%|██████████████████████████████████▋        | 80/99 [29:46<14:16, 45.05s/it]----loss:0.05166514063045369---
 82%|███████████████████████████████████▏       | 81/99 [30:35<13:52, 46.24s/it]----loss:0.05159448848545817---
 83%|███████████████████████████████████▌       | 82/99 [31:31<13:54, 49.08s/it]----loss:0.05152509710301109---
 84%|████████████████████████████████████       | 83/99 [32:24<13:24, 50.29s/it]----loss:0.05145693046192346---
 85%|████████████████████████████████████▍      | 84/99 [33:14<12:32, 50.16s/it]----loss:0.051389953944931024---
 86%|████████████████████████████████████▉      | 85/99 [34:11<12:12, 52.33s/it]----loss:0.051324134269764315---
 87%|█████████████████████████████████████▎     | 86/99 [35:07<11:32, 53.24s/it]----loss:0.051259439424283154---
 88%|█████████████████████████████████████▊     | 87/99 [35:55<10:22, 51.84s/it]----loss:0.05119583860539704---
 89%|██████████████████████████████████████▏    | 88/99 [36:45<09:23, 51.25s/it]----loss:0.051133302161514356---
 90%|██████████████████████████████████████▋    | 89/99 [37:39<08:39, 51.92s/it]----loss:0.05107180153828329---
 91%|███████████████████████████████████████    | 90/99 [38:32<07:51, 52.41s/it]----loss:0.051011309227404475---
 92%|███████████████████████████████████████▌   | 91/99 [39:29<07:10, 53.79s/it]----loss:0.05095179871831452---
 93%|███████████████████████████████████████▉   | 92/99 [40:24<06:19, 54.20s/it]----loss:0.05089324445255136---
 94%|████████████████████████████████████████▍  | 93/99 [41:26<05:39, 56.58s/it]----loss:0.05083562178062897---
 95%|████████████████████████████████████████▊  | 94/99 [42:23<04:43, 56.65s/it]----loss:0.05077890692126074---
 96%|█████████████████████████████████████████▎ | 95/99 [43:19<03:44, 56.24s/it]----loss:0.05072307692278237---
 97%|█████████████████████████████████████████▋ | 96/99 [44:14<02:47, 55.97s/it]----loss:0.05066810962663606---
 98%|██████████████████████████████████████████▏| 97/99 [45:10<01:52, 56.11s/it]----loss:0.0506139836327878---
 99%|██████████████████████████████████████████▌| 98/99 [46:07<00:56, 56.23s/it]----loss:0.05056067826695867---
100%|███████████████████████████████████████████| 99/99 [47:10<00:00, 28.59s/it]

Process finished with exit code 0

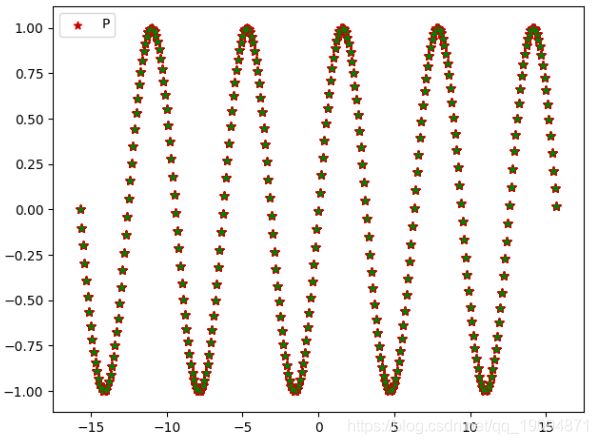
上面损失函数值有下降，但越到后面下降幅度越小！
这个图的legend每设置好，抱歉！红色五角星是x - sin(x)曲线，而绿色圆圈是x-预测值y，图中可以看到两个已经重合了。

代码二：添加Batch训练,替换激活函数

这里例子预测sin曲线，如果用relu作为激活函数，效果会很差，建议用sigmoid或者Prule。因为，sin曲线有一般为负数，relu激活函数在神经元输出为负数时激活为0，这会导致反向传播有些神经元梯度为0，不更新参数。

# -*- coding: utf-8 -*-
'''
    20191119
    构建简单的全连接神经网络，实现前向计算和反向传播算法求导
'''
import numpy as np
import math
import matplotlib.pyplot as plt
# from tqdm import tqdm
import tqdm
class SimpleNerworks:
    '''
    我希望实例化这个类的时候，你就想好了网络的层数，以及每层网络的神经元个数
    '''
    def __init__(self,*kwargs):
        super(SimpleNerworks, self).__init__()
        assert len(kwargs)>=2
        #初始化权重和偏差
        self.weights = [np.mat(np.random.randn(y,x),dtype=float) for x,y in zip(kwargs[:-1],kwargs[1:])]
        self.bias = [np.mat(np.random.randn(y,1),dtype=float) for y in kwargs[1:]]
        # print(self.weights)
        # print(self.bias)
        self.a = [np.mat(np.zeros((y,1)),dtype=float) for y in kwargs] #每个神经元的输出值，输入层直接是x，其他层则为a = sigmoid(z)
        self.z = [np.mat(np.zeros_like(b),dtype=float) for b in self.bias] #每个神经元的输入值，输入层就算了，z = wx+b
        self.delta = [np.mat(np.zeros_like(b),dtype=float) for b in self.bias]

        #梯度
        self.delta_bias = [np.mat(np.zeros_like(b)) for b in self.bias]
        self.delta_weights = [np.mat(np.zeros_like(w)) for w in self.weights]

    def forward(self,put_batch:list,Mode_Train=True):
        #Mode_Train表示模型状态，如果为True，则计算前向运算时，保存中间值a,z,并用反向传播计算出所有参数梯度。否则不保存。
        #put为一个list对象，也就是一个batch,数据存放形式像这样[(x_1,y_1),(x_2,y_2),...]，
        out = []
        loss = []
        for x, y in put_batch:
            # 输入x，y要规范成矩阵，方便运算！
            x = np.mat(x)
            y = np.mat(y)
            # 每一次前向运算都可以利用后向运算把对于梯度求出来。
            self.a[0] = x
            for i, (w, b) in enumerate(zip(self.weights,self.bias)):
                self.z[i] = w.dot(self.a[i]) + b
                self.a[i + 1] = self.s(self.z[i])
            if Mode_Train:
                # 后向运算计算所有参数的梯度
                delta_weights, delta_bias = self.backpropagation(self.a[-1], y)
                # 梯度累积
                self.delta_weights = [w + nw for w, nw in zip(self.delta_weights, delta_weights)]
                self.delta_bias = [b + nb for b, nb in zip(self.delta_bias, delta_bias)]
            out.append(self.a[-1])
            loss.append(self.loss_function(self.a[-1],y))
        return out,np.sum(loss)

    def Zero_gradient(self):
        '''梯度清零'''
        self.delta_weights = [w*0 for w in self.delta_weights]
        self.delta_bias = [b * 0 for b in self.delta_bias]
    def backpropagation(self,y_pre,y_real):
        '''
        反向传播
        计算出每个神经元的delta，按照反向传播公式求出所有梯度
        :return: 返回每个w，b的梯度
        '''

        #先算出最后一层的delta
        self.delta[-1] = np.multiply(self.loss_derivative(y_pre , y_real),self.s_derivative(self.z[-1]))

        #算出所有delta
        i = len(self.delta) -1
        while i>=1:
            self.delta[i-1] = np.multiply(np.dot(self.weights[i].T,self.delta[i]) , self.s_derivative(self.z[i-1]))
            i -= 1

        #利用delta算出所有参数的梯度
        delta_bias = self.delta
        delta_weights = [ D.dot(A.T) for D,A in zip(self.delta,self.a[:-1])]
        return delta_weights,delta_bias

    def updata_w_b(self,batch_size,lr):
        self.bias = [b - lr * (delta_b/batch_size) for b,delta_b in zip(self.bias,self.delta_bias)]
        self.weights = [w - lr*(delta_w/batch_size) for w, delta_w in zip(self.weights,self.delta_weights)]


    def s(self,x):
        # x =  self.Rule(x)
        x = self.Sigmoid(x)
        # x = self.leakyRelu(x)
        return x

    def s_derivative(self,x):
        # x = self.Rule_derivative(x)
        x = self.Sigmoid_derivative(x)
        # x = self.leakyRelu_derivative(x)
        return x

    def Rule(self,x):
        return np.maximum(x, 0)

    def Rule_derivative(self,x):
        return (x > 0) +0.

    def leakyRelu(self,x):
        a = np.where(x < 0, 0.5 * x, x)
        return a

    def leakyRelu_derivative(self,x):
        a = np.where(x < 0, 0.5, 1.)
        return a

    def Sigmoid(self,x):
        #sigmoid函数
        s = 1 / (1 + np.exp(-x))
        return s

    def Sigmoid_derivative(self,x):
        # sigmoid函数对x的求导
        return np.multiply(self.Sigmoid(x),1 - self.Sigmoid(x))

    def loss_function(self,y_pre,y_real):
        '''
        :param y_pre: 网络计算值
        :param y_real: 真实值
        :return: 1/2 *(y_pre-y_real)^2
        这里我之所以前面乘以1/2，是因为，这样loss对里面的y_pre求导，刚好等于y_pre-y_real，十分简洁
        '''
        return 0.5*pow(y_pre-y_real,2).sum()

    def loss_derivative(self,y_pre,y_real):
        return y_pre-y_real

    def BCL_cross_entropy(self,y_pre,y_real):
        '''
        二分类交叉熵损失函数
        :param y_pre:经过softmoid之后，将值变为0~1之间
        :param y_real: 0或者1
        :return:
        '''
        #为了防止log(0)出现，将里面的概率进行处理
        y_pre = np.clip(y_pre,1e-12,1. - 1e-12)
        loss = -np.sum(y_real * np.log(y_pre) + (1 - y_real) * np.log(1 - y_pre))
        return loss

    def MCL_cross_entropy(self,y_pre,y_real):
        '''
        多分类交叉熵,用多分类交叉熵做损失函数必须最后一层用softmax激活函数
        :param y_pre: one-hot类型，里面的值都在0~1之间
        :param y_real: one-hot类型
        :return:
        '''
        # 为了防止log(0)出现，将里面的概率进行处理
        y_pre = np.clip(y_pre, 1e-12, 1. - 1e-12)
        loss = -np.sum(y_real * np.log(y_pre))
        return loss

    def Softmax(self,layer_z):
        exp_z = np.exp(layer_z)
        return exp_z / np.sum(exp_z)

    def SaveModel(self):
        np.savez('parameter.npz',self.weights,self.bias)
        # np.save('parameter_weights.npz',self.weights)
        # np.save('parameter_bias.npz',self.bias)
    def LoadModel(self):
        data = np.load('parameter.npz',allow_pickle=True)
        self.weights = data['arr_0']
        self.bias = data['arr_1']

def DataSinX():
    '''
    生成x,sin(x),打乱。
    :return:
    '''
    data = [(i,math.sin(i)) for i in np.arange(-5 * math.pi, 5 * math.pi, 0.1)