机器学习基础（七）：概率图模型（HMM、MRF、CRF、话题模型、推断方法）

7、概率图模型

概率模型probabilistic model：提供一种描述框架，将学习任务归结于计算变量的概率分布，核心是如何基于可观测变量推测出未知变量的条件分布 →

①生成式generative模型：考虑联合分布P(Y,R,O)
②判别式discriminative模型：考虑条件分布P(Y,R|O)
由①或②得到条件概率分布P(Y|O)
（Y：所关心的变量集合；O：可观测变量集合；R：其他变量的集合）

概率图模型probabilistic graphical model：一类用图来表达变量相关关系的概率模型。表示工具：图，常见用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”
①有向无环图表示变量间的依赖关系→有向图模型/贝叶斯网
②无向图表示变量间的相关关系→无向图模型/马尔可夫网

7.1隐马尔可夫模型Hidden Markov Model，HMM

结构最简单的动态贝叶斯网dynamic Bayesian network，生成式有向图模型，主要用于时序数据建模（语音识别、自然语言处理等领域）

→属于“马尔可夫链”：系统下一时刻的状态仅由当前状态决定，不依赖与以往的任何状态

→所有变量的联合概率分布为：



→基于式(14.1)的条件独立性，隐马尔可夫模型的这三个问题均能被高效求解

7.2马尔可夫随机场Markov Random Field，MRF

典型的马尔可夫网，生成式无向图模型

7.2.1势函数potential functions/因子factor

定义在变量子集上的非负实函数，主要用于定义概率分布函数，需要在所偏好的变量取值上有较大函数值→

为满足非负性，指数函数常被用于定义势函数：

7.2.2

多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关

若变量个数较多，则团的数目将会很多，意味着会有很多乘积项，会给计算带来负担 →

7.2.3

分离集separating set：若从结点集A中的结点到B中的结点都必须经过结点集C中的结点，则称结点集A和B被结点集C分离，C称为分离集

全局马尔可夫性global Markov property：给定两个变量子集的分离集，则这两个变量子集条件独立，即下图的xA⊥xB | xC（A,B,C对应的变量集分别为xA,xB,xC）

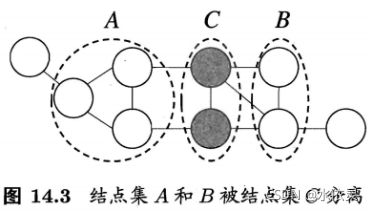
推论：①局部马尔可夫性：给定某变量的邻接变量，则该变量条件独立于其他变量
②成对马尔可夫性：给定所有其他变量，两个非邻接变量条件独立

7.3条件随机场Conditional Random Filed，CRF

对多个变量在给定观测之后的条件概率进行建模，判别式无向图模型

观测序列x={x1,x2,…,xn}，相应的标记序列y={y1,y2,…,yn}（可以是结构型变量，即其分量之间具有某种关联性），目标是构建条件概率模型P(y|x)

常用图G结构：链式结构（链式条件随机场chain-structured CRF）

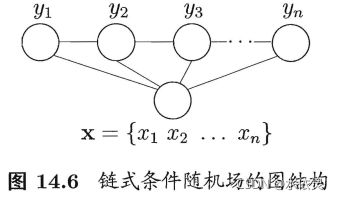
主要包含两种关于标记变量的团，通过选用指数势函数并引入特征函数（特征函数通常是实值函数，以刻画数据的一些很可能成立或期望成立的经验特性），条件概率被定义为：

7.4话题模型topic model

用于处理离散型的数据，生成式有向图模型

典型代表：隐狄利克雷分配模型（LDA），从生成式模型的角度看待文档和话题

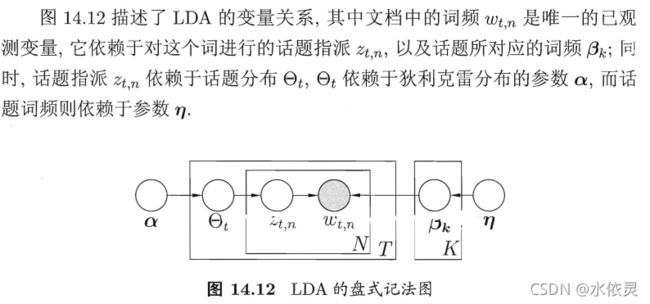
7.5概率图模型的推断方法

7.5.1精确推断方法

希望能计算出目标变量的边际分布或条件分布的精确值，算法复杂度随着极大团规模的增长呈指数增长，适用范围有限

7.5.1.1变量消去

最直观的精确推断算法，也是构建其他精确推断算法的基础

通过利用乘法对加法的分配律，变量消去法把多个变量的积的求和问题，转化为对部分变量交替进行求积与求和的问题。这种转化使得每次的求和与求积运算限制在局部，仅与部分变量有关，从而简化了计算：


缺点：若需计算多个边际分布，重复使用变量消去法将会造成大量的冗余计算

7.5.1.2信念传播

将变量消去法中的求和操作看作一个消息传递过程，较好地解决了求解多个边际分布时的重复计算问题

若圈结构中没有环，则信念传播算法经过两个步骤即可完成所有消息传递，进而能计算所有变量上的边际分布：①指定一个根结点，从所有叶结点开始向根结点传递消息，直到根结点收到所有邻接结点的消息; ②从根结点开始向叶结点传递消息，直到所有叶结点均收到消息

7.5.2近似推断方法

希望在较低的时间复杂度下获得原问题的近似解，更常用

7.5.2.1采样

通过使用随机化方法完成近似

“若直接计算或逼近这个期望比推断概率分布更容易，则直接操作无疑将使推断问题的求解更为高效”

概率图模型中最常用的采样技术是马尔可夫链蒙特卡罗（MCMC）方法：

→ MCMC方法先设法构造一条马尔可夫链，使其收敛至平稳分布恰为待估计参数的后验分布，然后通过这条马尔可夫链来产生符合后验分布的样本，并基于这些样本来进行估计。这里马尔可夫链转移概率的构造至关重要，不同的构造方法将产生不同的MCMC算法

MH算法（MCMC的重要代表）：基于“拒绝采样”来逼近平稳分布p
吉布斯采样：有时被视为MH算法的特例

7.5.2.2变分推断variational inference

使用确定性近似完成近似推断。通过使用已知简单分布来逼近需推断的复杂分布，并通过限制近似分布的类型，从而得到一种局部最优、但具有确定解的近似后验分布

盘式记法plate notation：概率图模型一种简洁的表示方法

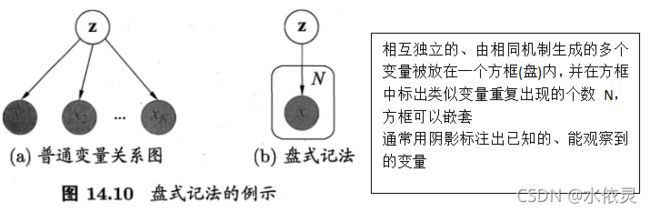
一般来说，上图所对应的推断和学习任务主要是由观察到的变量x来估计隐变量和分布参数变量，即求解p(z | x,θ)和θ

_ _ _ _ _ _ 未完待续，喜欢的朋友可以关注后续文章 _ _ _ _ _ _

机器学习基础系列文章回顾：
机器学习基础（一）：简介
机器学习基础（二）：模型评估与选择
机器学习基础（三）：决策树
机器学习基础（四）：特征选择与稀疏学习
机器学习基础（五）：计算学习理论（PAC学习、有限假设空间、VC维、Rademacher复杂度、稳定性）
机器学习基础（六）：贝叶斯分类（贝叶斯决策论、朴素/半朴素贝叶斯分类器、贝叶斯网、EM算法）

参考书目：
周志华.《机器学习》