人工智能与机器学习---用线性LDA、k-means和SVM算法进行二分类可视化分析

一、支持向量机 （SVM）算法的原理

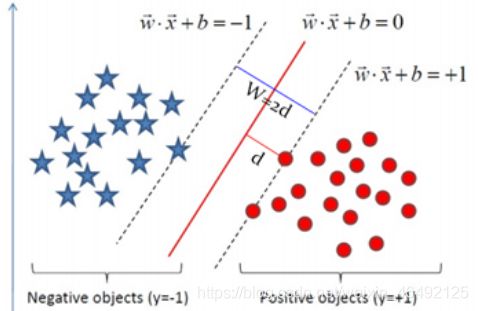
支持向量机（Support Vector Machine，常简称为SVM）是一种监督式学习的方法，可广泛地应用于统计分类以及回归分析。它是将向量映射到一个更高维的空间里，在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面，分隔超平面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大，分类器的总误差越小。

1、支持向量机的基本思想

对于线性可分的任务，找到一个具有最大间隔超平面，如图所示

2、步骤

（1）导入数据；

（2）数据归一化；

（3）执行svm寻找最优的超平面；

（4）绘制分类超平面核支持向量；

（5）利用多项式特征在高维空间中执行线性svm；

（6）选择合适的核函数，执行非线性svm。

3、算法优缺点：

算法优点：　　
（1）使用核函数可以向高维空间进行映射；
（2）使用核函数可以解决非线性的分类；
（3）分类思想很简单，就是将样本与决策面的间隔最大化；
（4）分类效果较好。

算法缺点：
（1）SVM算法对大规模训练样本难以实施；
（2）用SVM解决多分类问题存在困难；
（3）对缺失数据敏感，对参数和核函数的选择敏感。

二、线性LDA进行二分类可视化分析

1、对鸢尾花数据集进行分类

（1）python代码

#基于线性LDA算法对鸢尾花数据集进行分类
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import preprocessing
dataset = pd.read_csv(r'http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data')
X = dataset.values[:, :-1]
y = dataset.values[:, -1]
le = preprocessing.LabelEncoder()
le.fit(['Iris-setosa', 'Iris-versicolor', 'Iris-virginica'])
y = le.transform(y)
X = X[:, :2] 
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
  
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
  
# Applying LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components = 2)
X_train = lda.fit_transform(X_train, y_train)
X_test = lda.transform(X_test)
  
# Fitting Logistic Regression to the Training set
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
  
# Predicting the Test set results
y_pred = classifier.predict(X_test)
  
# Making the Confusion Matrix
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
  
# Visualising the Training set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
                     np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
                c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.legend()
plt.show()

（2）运行结果

2、对月亮数据集进行分类

（1）python代码

#基于线性LDA算法对月亮数据集进行分类
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from mpl_toolkits.mplot3d import Axes3D
def LDA(X, y):
    X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
    X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
    len1 = len(X1)
    len2 = len(X2)
    mju1 = np.mean(X1, axis=0)#求中心点
    mju2 = np.mean(X2, axis=0)
    cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
    cov2 = np.dot((X2 - mju2).T, (X2 - mju2))
    Sw = cov1 + cov2
    w = np.dot(np.mat(Sw).I,(mju1 - mju2).reshape((len(mju1),1)))# 计算w
    X1_new = func(X1, w)
    X2_new = func(X2, w)
    y1_new = [1 for i in range(len1)]
    y2_new = [2 for i in range(len2)]
    return X1_new, X2_new, y1_new, y2_new
def func(x, w):
    return np.dot((x), w)
if '__main__' == __name__:
    X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
    X1_new, X2_new, y1_new, y2_new = LDA(X, y)
    plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
    plt.show()
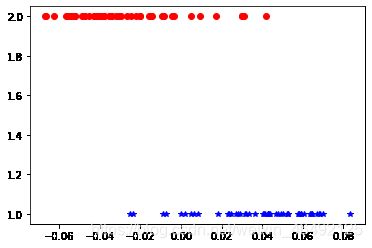
    plt.plot(X1_new, y1_new, 'b*')
    plt.plot(X2_new, y2_new, 'ro')
    plt.show()

（2）运行结果

三、k-means进行二分类可视化分析

1、对鸢尾花数据集进行分类

（1）python代码

import matplotlib.pyplot as plt  
import numpy as np  
from sklearn.cluster import KMeans
from sklearn import datasets 
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data[:, 2:4] ##表示我们只取特征空间中的后两个维度
print(X.shape)
#绘制数据分布图
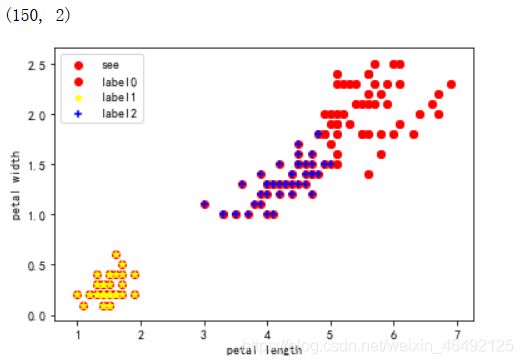
plt.scatter(X[:, 0], X[:, 1], c = "red", marker='o', label='see')  
plt.xlabel('petal length')  
plt.ylabel('petal width')  
plt.legend(loc=2)  
estimator = KMeans(n_clusters=3)#构造聚类器
estimator.fit(X)#聚类
label_pred = estimator.labels_ #获取聚类标签
#绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')  
plt.scatter(x1[:, 0], x1[:, 1], c = "yellow", marker='*', label='label1')  
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')  
plt.xlabel('petal length')  
plt.ylabel('petal width')  
plt.legend(loc=2)  
plt.show()  

（2）运行结果

2、对月亮数据集进行分类

（1）python代码

# -*- coding:utf-8 -*-
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
 
# 导入月亮型数据(证明kmean不能很好对其进行聚类)
X,y = make_moons(n_samples=200,random_state=0,noise=0.05)
print(X.shape)
print(y.shape)
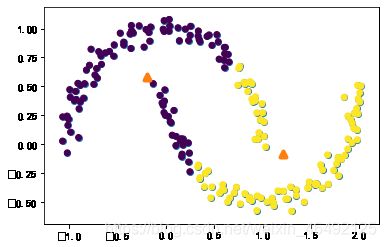
plt.scatter(X[:,0],X[:,1])
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
y_pred = kmeans.predict(X)
cluster_center = kmeans.cluster_centers_
plt.scatter(X[:,0],X[:,1],c=y_pred)
plt.scatter(cluster_center[:,0],cluster_center[:,1],marker='^',linewidth=4)
plt.show()

（2）运行结果

四、SVM算法进行二分类可视化分析

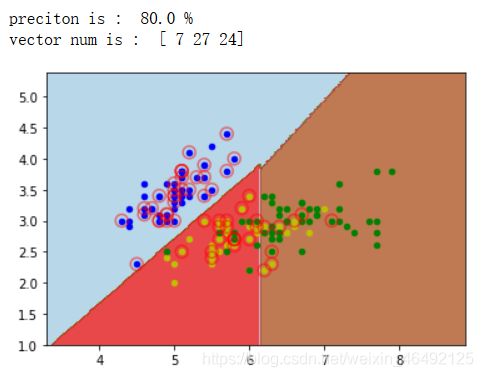
1、对鸢尾花数据集进行分类

（1）python代码

from sklearn.svm import SVC
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
def plot_point2(dataArr, labelArr, Support_vector_index):
    for i in range(np.shape(dataArr)[0]):
        if labelArr[i] == 0:
            plt.scatter(dataArr[i][0], dataArr[i][1], c='b', s=20)
        elif labelArr[i] == 1:
            plt.scatter(dataArr[i][0], dataArr[i][1], c='y', s=20)
        else:
            plt.scatter(dataArr[i][0], dataArr[i][1], c='g', s=20)
    
    for j in Support_vector_index:
        plt.scatter(dataArr[j][0], dataArr[j][1], s=100, c='', alpha=0.5, linewidth=1.5, edgecolor='red')
    plt.show()
if __name__ == "__main__":
    iris = load_iris()
    x, y = iris.data, iris.target
    x = x[:, :2]
    X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
    clf = SVC(C=1, cache_size=200, class_weight=None, coef0=0.0,
                decision_function_shape='ovr', degree=3, gamma=0.1,
                kernel='linear', max_iter=-1, probability=False, random_state=None,
                shrinking=True, tol=0.001, verbose=False)
    # 调参选取最优参数
    # clf = GridSearchCV(SVC(), param_grid={"kernel": ['rbf', 'linear', 'poly', 'sigmoid'],
    #                                       "C": [0.1, 1, 10], "gamma": [1, 0.1, 0.01]}, cv=3)
    clf.fit(X_train, y_train)
 
    # print("The best parameters are %s with a score of %0.2f" % (clf.best_params_, clf.best_score_))
 
    predict_list = clf.predict(X_test)
 
    precition = clf.score(X_test, y_test)
    print("preciton is : ", precition * 100, "%")
 
    n_Support_vector = clf.n_support_
    print("vector num is : ", n_Support_vector)
    Support_vector_index = clf.support_
 
    x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    h = 0.02
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
    plot_point2(x, y, Support_vector_index)

（2）运行结果

2、对月亮数据集进行分类

（1）python代码

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
polynomial_svm_clf = Pipeline([
        # 将源数据 映射到 3阶多项式
        ("poly_features", PolynomialFeatures(degree=3)),
        # 标准化
        ("scaler", StandardScaler()),
        # SVC线性分类器
        ("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
    ])
polynomial_svm_clf.fit(X, y)
def plot_dataset(X, y, axes):
    plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
    plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
    plt.axis(axes)
    plt.grid(True, which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
   # plt.title("月亮数据",fontsize=20)
def plot_predictions(clf, axes):
    # 打表
    x0s = np.linspace(axes[0], axes[1], 100)
    x1s = np.linspace(axes[2], axes[3], 100)
    x0, x1 = np.meshgrid(x0s, x1s)
    X = np.c_[x0.ravel(), x1.ravel()]
    y_pred = clf.predict(X).reshape(x0.shape)
    y_decision = clf.decision_function(X).reshape(x0.shape)
#     print(y_pred)
#     print(y_decision)
    plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
    plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()

（2）运行结果