利用t-sne算法和散点图工具对高维数据的可视化分析
利用t-sne算法和散点图工具对高维数据的可视化分析
- 前言
- python散点图工具seaborn和sklearn实现的t-SNE
- 推荐一个算法推演t-SNE的实例
- 其他参考和收录:
前言
这是一篇汇总性质的资料收集,将t-sne和散点图工具的资料传一下。t-SNE是基于t分布(t distributed)的随机邻近嵌入(StochasticNeighborEmbedding),StochasticNeighborEmbedding是杰弗雷辛顿(GeoffreyHinton)在2003年主笔提出来的降维方法,t-SNE是Laurens van der Maaten是在此基础上改进的数据降维技术,尤其在神经网络embedding的高维数据分析方面,已经成为标配。所以很多平台和网站都有介绍,并且结合散点图可以很直观的分析出来模型和数据的分布情况。
python散点图工具seaborn和sklearn实现的t-SNE
对seanborn的介绍直接引自Seaborn中文网站, 这是一个基于 matplotlib 且数据结构与 pandas 统一的统计图制作库, seaborn 的功能大致如下:
计算多变量间关系的面向数据集接口
可视化类别变量的观测与统计
可视化单变量或多变量分布并与其子数据集比较
控制线性回归的不同因变量并进行参数估计与作图
对复杂数据进行易行的整体结构可视化
对多表统计图的制作高度抽象并简化可视化过程
提供多个内建主题渲染 matplotlib 的图像样式
提供调色板工具生动再现数据
Seaborn 框架旨在以数据可视化为中心来挖掘与理解数据。它提供的面向数据集制图函数主要是对行列索引和数组的操作,包含对整个数据集进行内部的语义映射与统计整合,以此生成富于信息的图表。
用sklearn实现的t-SNE非常方便和简单。
import seaborn as sns
from sklearn.datasets import load_iris,load_digits
X, y = load_digits(return_X_y=True)
X_embedded = tsne.fit_transform(X)
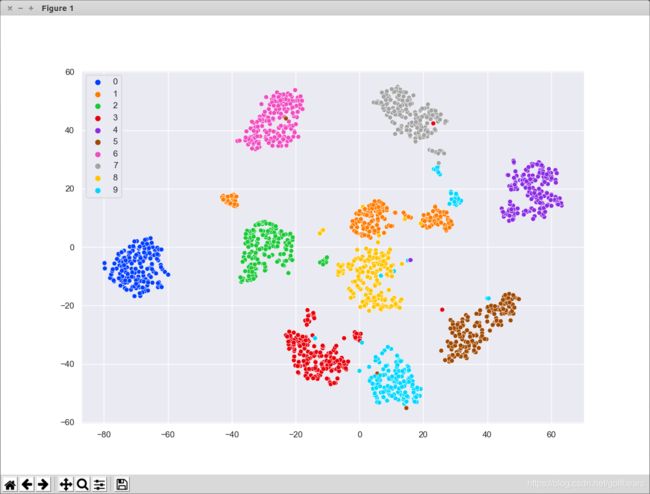
区区几行代码就实现了对一个64维度数据的降维,后面的实例会画出这个降维后的数据散点图。
推荐一个算法推演t-SNE的实例
推荐这个网站t-SNE Python Example的算法介绍,python代码实测有效,我整理了一下,贴在下面:
import numpy as np
from sklearn.datasets import load_iris,load_digits
from scipy.spatial.distance import pdist
from sklearn.manifold.t_sne import _joint_probabilities
from scipy import linalg
from sklearn.metrics import pairwise_distances
from scipy.spatial.distance import squareform
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from matplotlib import pyplot as plt
import seaborn as sns
def fit(X):
n_samples = X.shape[0]
# Compute euclidean distance
distances = pairwise_distances(X, metric='euclidean', squared=True)
# Compute joint probabilities p_ij from distances.
P = _joint_probabilities(distances=distances, desired_perplexity=perplexity, verbose=False)
# The embedding is initialized with iid samples from Gaussians with standard deviation 1e-4.
X_embedded = 1e-4 * np.random.mtrand._rand.randn(n_samples, n_components).astype(np.float32)
# degrees_of_freedom = n_components - 1 comes from
# "Learning a Parametric Embedding by Preserving Local Structure"
# Laurens van der Maaten, 2009.
degrees_of_freedom = max(n_components - 1, 1)
return _tsne(P, degrees_of_freedom, n_samples, X_embedded=X_embedded)
def _tsne(P, degrees_of_freedom, n_samples, X_embedded):
params = X_embedded.ravel()
obj_func = _kl_divergence
params = _gradient_descent(obj_func, params, [P, degrees_of_freedom, n_samples, n_components])
X_embedded = params.reshape(n_samples, n_components)
return X_embedded
def _kl_divergence(params, P, degrees_of_freedom, n_samples, n_components):
X_embedded = params.reshape(n_samples, n_components)
dist = pdist(X_embedded, "sqeuclidean")
dist /= degrees_of_freedom
dist += 1.
dist **= (degrees_of_freedom + 1.0) / -2.0
Q = np.maximum(dist / (2.0 * np.sum(dist)), MACHINE_EPSILON)
# Kullback-Leibler divergence of P and Q
kl_divergence = 2.0 * np.dot(P, np.log(np.maximum(P, MACHINE_EPSILON) / Q))
# Gradient: dC/dY
grad = np.ndarray((n_samples, n_components), dtype=params.dtype)
PQd = squareform((P - Q) * dist)
for i in range(n_samples):
grad[i] = np.dot(np.ravel(PQd[i], order='K'), X_embedded[i] - X_embedded)
grad = grad.ravel()
c = 2.0 * (degrees_of_freedom + 1.0) / degrees_of_freedom
grad *= c
return kl_divergence, grad
def _gradient_descent(obj_func, p0, args, it=0, n_iter=1000,
n_iter_check=1, n_iter_without_progress=300,
momentum=0.8, learning_rate=200.0, min_gain=0.01,
min_grad_norm=1e-7):
p = p0.copy().ravel()
update = np.zeros_like(p)
gains = np.ones_like(p)
error = np.finfo(np.float).max
best_error = np.finfo(np.float).max
best_iter = i = it
for i in range(it, n_iter):
error, grad = obj_func(p, *args)
grad_norm = linalg.norm(grad)
inc = update * grad < 0.0
dec = np.invert(inc)
gains[inc] += 0.2
gains[dec] *= 0.8
np.clip(gains, min_gain, np.inf, out=gains)
grad *= gains
update = momentum * update - learning_rate * grad
p += update
print("[t-SNE] Iteration %d: error = %.7f,"
" gradient norm = %.7f"
% (i + 1, error, grad_norm))
if error < best_error:
best_error = error
best_iter = i
elif i - best_iter > n_iter_without_progress:
break
if grad_norm <= min_grad_norm:
break
return p
sns.set(rc={'figure.figsize':(11.7,8.27)})
palette = sns.color_palette("bright", 10)
X, y = load_digits(return_X_y=True)
MACHINE_EPSILON = np.finfo(np.double).eps
n_components = 2
perplexity = 30
tsne = TSNE()
X_embedded = tsne.fit_transform(X)
#X_embedded = fit(X)
sns.scatterplot(X_embedded[:,0], X_embedded[:,1], hue=y, legend='full', palette=palette)
digits = load_digits()
X_tsne = TSNE(n_components=2,random_state=33).fit_transform(digits.data)
X_pca = PCA(n_components=2).fit_transform(digits.data)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=digits.target,label="t-SNE")
plt.legend()
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=digits.target, label="PCA")
plt.legend()
plt.savefig('images/digits_tsne-pca.png', dpi=120)
plt.show()
pass
上述代码还结合了知乎上的一篇文章无监督学习之t-SNE加入了PCA方法的对比,更加衬托出t-SNE的神奇之处。

其他参考和收录:
1.t-SNE完整笔记
2.seaborn学习笔记2-散点图Scatterplot
3.seaborn.color_palette
4.Seaborn 学习笔记(1.0)
5.seaborn系列 (2) | 散点图scatterplot()