ML - 多项式回归

---

由来

线性回归的局限性：要求数据背后存在关系。
但在实际情况下，很少有有强相关性的数据集。更多是具有非线性关系。
可以使用 多项式回归 的方法，改进线性回归法，使得可以对非线性的数据进行处理和预测，解决模型泛化相关的问题。

---

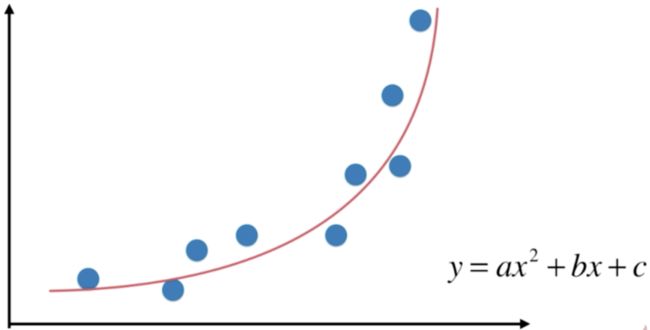
什么是多项式回归

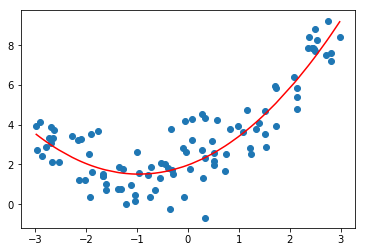
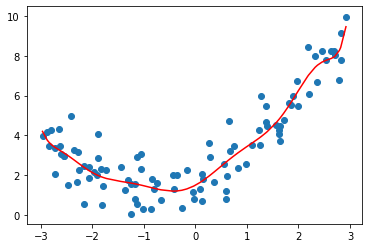
上述数据使用二次曲线来拟合，效果更好。
从x 的角度来看是一个非线性方程。
如果将 $x^2$理解为一个特征，$x$ 理解为另一个特征，依然可以看做线性方程。
多项式回归：为样本多添加了一些特征，这些特征是原来样本的 多项式组合，使用线性回归的思路 更好的拟合数据。
相比降维，多项式有升维的效果。

---

代码实现多项式回归

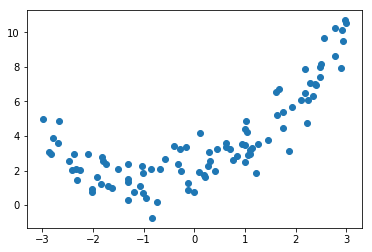
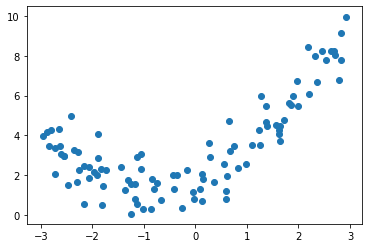
创建数据

import numpy as np 
import matplotlib.pyplot as plt
 
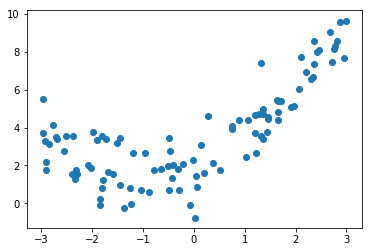
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
 
plt.scatter(x, y)
plt.show()

---

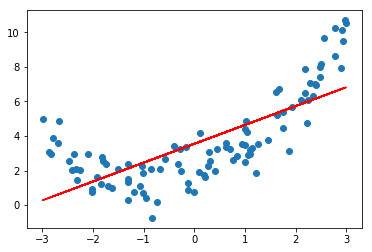
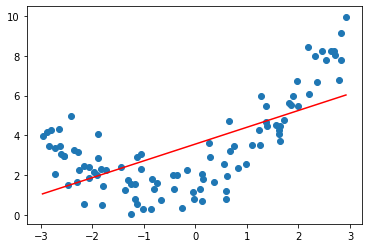
使用线性回归拟合数据

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
 
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

---

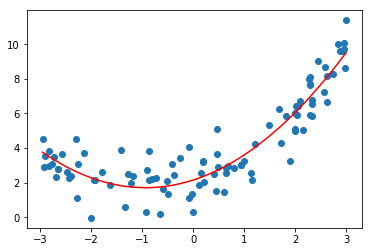
添加一个特征 $x^2$

X2 = np.hstack([X, X**2])
 
X2.shape
# (100, 2)

 
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
 
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r') # y_predict2[np.argsort(x)] 将x排序后的索引，给y当索引来取值
plt.show()

lin_reg2.coef_
# array([ 0.99870163,  0.54939125])
 
lin_reg2.intercept_
# 1.8855236786516001

---

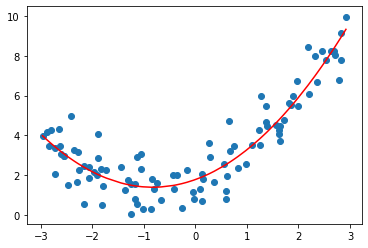
scikit-learn中的多项式回归和Pipeline

import numpy as np 
import matplotlib.pyplot as plt
 
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)
 
from sklearn.preprocessing import PolynomialFeatures
 
poly = PolynomialFeatures(degree=2) # 添加二次幂的特征（原本只有一次）
poly.fit(X)
X2 = poly.transform(X)

X2.shape
# (100, 3)
 
X[:5,:]
'''
    array([[-2.95649576],
           [ 2.86800948],
           [ 0.5426261 ],
           [ 2.97500577],
           [ 1.1201316 ]])
'''

 
X2[:5,:] # 增加第一列特征为1，第二列为x，第三列为 x^2
'''
    array([[ 1.        , -2.95649576,  8.74086716],
           [ 1.        ,  2.86800948,  8.22547841],
           [ 1.        ,  0.5426261 ,  0.29444309],
           [ 1.        ,  2.97500577,  8.85065935],
           [ 1.        ,  1.1201316 ,  1.25469479]])
'''

 
from sklearn.linear_model import LinearRegression

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
 
lin_reg2.coef_
# array([ 0.        ,  0.9460157 ,  0.50420543])
 
lin_reg2.intercept_  # 2.1536054095953823

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

---

PolynomialFeatures 类的使用

X = np.arange(1, 11).reshape(-1, 2) 
X
'''
  array([[ 1,  2],
           [ 3,  4],
           [ 5,  6],
           [ 7,  8],
           [ 9, 10]])
'''
 
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)
 
X2.shape
# (5, 6) 
 
X2 # 1，x1, x2, x1^2, x1 * x2, x2^2 
'''
    array([[  1.,   1.,   2.,   1.,   2.,   4.],
           [  1.,   3.,   4.,   9.,  12.,  16.],
           [  1.,   5.,   6.,  25.,  30.,  36.],
           [  1.,   7.,   8.,  49.,  56.,  64.],
           [  1.,   9.,  10.,  81.,  90., 100.]])
'''

 
poly = PolynomialFeatures(degree=3)
poly.fit(X)
X3 = poly.transform(X)
X3.shape
# (5, 10)

 
X3 # 1，x1, x2, x1^2, x1 * x2, x2^2, x1^3, x1^2 * x2, x2^2 * x1  , x2^3
'''
    array([[   1.,    1.,    2.,    1.,    2.,    4.,    1.,    2.,    4.,
               8.],
           [   1.,    3.,    4.,    9.,   12.,   16.,   27.,   36.,   48.,
              64.],
           [   1.,    5.,    6.,   25.,   30.,   36.,  125.,  150.,  180.,
             216.],
           [   1.,    7.,    8.,   49.,   56.,   64.,  343.,  392.,  448.,
             512.],
           [   1.,    9.,   10.,   81.,   90.,  100.,  729.,  810.,  900.,
            1000.]])
'''

---

Pipeline

如果degree 特别大，数据之间的差距就会很大。数据不均衡，搜索会很慢。此时最好使用数据的归一化，然后再送给线性回归。
pipeline 会将这三步合在一起。

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

poly_reg = Pipeline([ # 列表中是元组
    ("poly", PolynomialFeatures(degree=2)), 
    ("std_scaler", StandardScaler()),
    ("lin_reg", LinearRegression())
])
 
poly_reg.fit(X, y)
y_predict = poly_reg.predict(X)
 
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

---

非线性拟合的陷阱

过度使用多项式回归，会造成过拟合和欠拟合的问题。
阶数越高，模型越复杂。
对于 kNN，k 越小越复杂，越大越简单。

---

过拟合和欠拟合

过拟合和欠拟合

import numpy as np
import matplotlib.pyplot as plt
 
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
 
plt.scatter(x, y)
plt.show()

---

使用线性回归

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)
# 0.42600823789139797

 
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

# 使用均方误差进行衡量

from sklearn.metrics import mean_squared_error

y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)
# 3.0245639566396174

---

使用多项式回归

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)
'''
Pipeline(memory=None,
             steps=[('poly',
                     PolynomialFeatures(degree=2, include_bias=True,
                                        interaction_only=False, order='C')),
                    ('std_scaler',
                     StandardScaler(copy=True, with_mean=True, with_std=True)),
                    ('lin_reg',
                     LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
                                      normalize=False))],
             verbose=False)
'''
 
y2_predict = poly2_reg.predict(X)
mean_squared_error(y, y2_predict)
# 0.7771936663502366
 
plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()

---

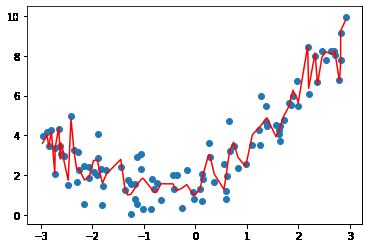
poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X, y)

y10_predict = poly10_reg.predict(X)
mean_squared_error(y, y10_predict)
# 0.7399087981911164
 
plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()

# 使用多项式线性回归 
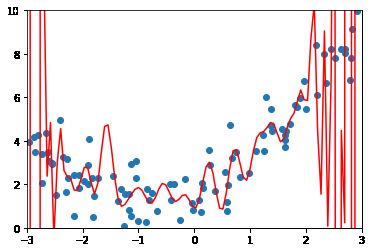
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)

y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict) # 误差很小  
# 0.3772280106840242
 
plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()

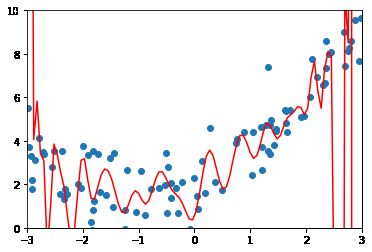
# 尝试还原曲线
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(X_plot)
 
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])
plt.show()

---

如何识别过拟合和欠拟合？
如何解决？ – 分离 训练和测试数据集

---

机器学习主要解决的是过拟合的问题；

泛化能力：由此及彼的能力。

---

train test split的意义

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
 
# 使用线性回归 并 测试均方误差
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
# 3.755594371740188
 
# 2阶多项式回归
poly2_reg.fit(X_train, y_train)
y2_predict = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# 1.103388026528141
 
# 10阶多项式 
poly10_reg.fit(X_train, y_train)
y10_predict = poly10_reg.predict(X_test)
mean_squared_error(y_test, y10_predict)
# 1.5723694744536456
 
# 100阶多项式 
poly100_reg.fit(X_train, y_train)
y100_predict = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict)
# 5.617460560638704e+20

---

为什么使用测试数据集

import numpy as np
import matplotlib.pyplot as plt
 
np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)
 
plt.scatter(x, y)
plt.show()

过拟合

from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
 
from sklearn.metrics import mean_squared_error

poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)

y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
# 0.68743577834336944
 
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly100_reg.predict(X_plot)
 
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 10])
plt.show()

模型的泛化能力差

---

train test split的意义

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
 
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
mean_squared_error(y_test, y_predict)
# 2.2199965269396573
 
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X_train, y_train)
y2_predict = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict)
# 0.80356410562978997
 
poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X_train, y_train)
y10_predict = poly10_reg.predict(X_test)
mean_squared_error(y_test, y10_predict)
# 0.92129307221507939
 
poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X_train, y_train)
y100_predict = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict)
# 14075796419.234262

---

如何判断？

模型复杂度 和 模型准确率 在 训练数据 和 测试数据上的表现。

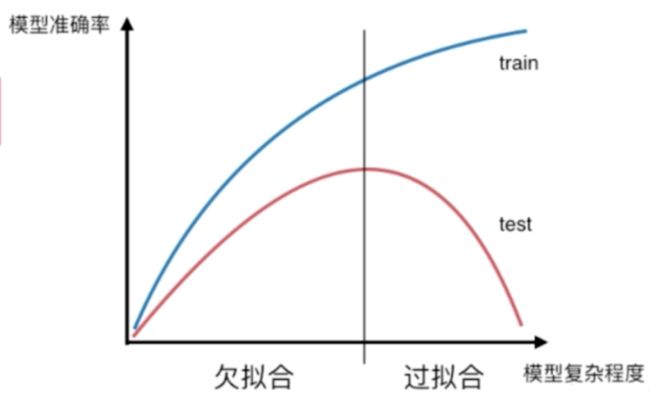
欠拟合 underfitting：算法所训练的模型 不能完整的表达数据关系。
过拟合 overfitting：算法过多的表达了数据间的关系（更多是噪音关系）。

上述曲线只是某个理论的模型，对于不同算法会有不同的曲线。
还有表达欠拟合和过拟合的方法：学习曲线。

---

学习曲线

随着训练样本的逐渐增多，算法训练出的模型的表现能力。

---