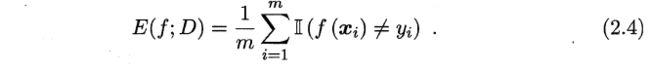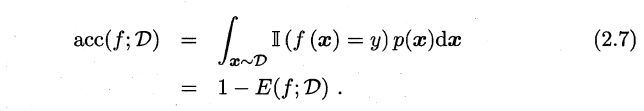ML (Chapter 2): 模型评估与选择

经验误差与过拟合

基本术语

• “错误率” (error rate): 分类错误的样本数占样本总数的比例，即如果在 $m$ 个样本中有 $\alpha$ 个样本分类错误，则错误率 $E=\alpha /m$
• 相应的，$1-\alpha /m$ 称为"精度" (accuracy)
• 我们把学习器的实际预测输出与样本的真实输出之间的差异称为"误差" (error) (误差期望)
  • 学习器在训练集上的误差称为"训练误差" (training error) 或 “经验误差” (empirical error)
  • 在新样本上的误差称为 “泛化误差” (generalization error)
  • 显然，我们希望得到泛化误差小的学习器. 然而，我们事先并不知道新样本是什么样，实际能做的是努力使经验误差最小化.在很多情况下，我们可以学得一个经验误差很小、在训练集上表现很好的学习器。遗憾的是，这样的学习器在多数情况下都不好. 我们实际希望的，是从训练样本中尽可能学出适用于所有潜在样本的"普遍规律". 然而，当学习器把训练样本学得"太好"了的时候，很可能巳经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降这种现象在机器学习中称为"过拟合" (overfitting). 与"过拟合"相对的是"欠拟合" (underfitting) ，这是指对训练样本的一般性质尚未学好
    
  • 欠拟合比较容易克服，例如在决策树学习中扩展分支、在神经网络学习中增加训练轮数等，而过拟合则很麻烦

损失函数和风险函数

损失函数 (loss function)

• 损失函数: 度量预测错误的程度，记作 $L(Y,f(X))$; 常用的损失函数:
  • (1) 0-1 损失函数 (0-1 loss function)
    
  • (2) 平方损失函数 (quadratic loss function)
    
  • (3) 绝对损失函数 (absolute loss function)
    
  • (4) 对数损失函数 (logarithmic loss function) 或 对数似然损失函数 (log-likelihood loss function)
    

---

风险函数 (risk function) / 泛化误差 (generalization error) / 期望损失(expected loss)

• 由于模型的输入、输出 $(X,Y)$ 是随机变量，遵循联合分布 $P(X,Y)$， 所以损失函数的期望是
  

---

经验风险 (empirical risk) / 经验损失 (empirical loss)

• 学习的目标就是选择期望风险最小的模型。由于联合分布 $P(X,Y)$ 是未知的， $R_{exp}(f)$ 不能直接计算。实际上，如果知道联合分布 $P(X,Y)$， 可以从联合分布直接求出条件概率分布 $P(Y|X)$， 也就不需要学习了。正因为不知道联合概率分布，所以才需要进行学习。这样一来，一方面根据期望风险最小学习模型要用到联合分布，另一方面联合分布又是未知的，所以监督学习就成为一个病态问题 (ill-formed problem)
• 给定一个训练数据集
  模型 $f(X)$ 关于训练数据集的平均损失称为经验风险 (empirical risk) 或经验损失 (empirical loss)，记作 $R_{emp}$:
  
  • e.g. 当损失函数为 0-1 损失函数时，经验风险就变成了 error rate
• 一个很自然的想法是用经验风险估计期望风险 。但是，由于现实中训练样本数目有限，甚至很小，所以用经验风险估计期望风险常常并不理想，要对经验风险进行一定的矫正。这就关系到监督学习的两个基本策略: 经验风险最小化和结构风险最小化

经验风险最小化与结构风险最小化

• Ref: 极大似然估计与最大后验概率估计

---

经验风险最小化 (Empirical risk minimization, ERM)

• 经验风险最小化的策略认为，经验风险最小的模型是最优的模型。根据这一策略，按照经验风险最小化求最优模型就是求解最优化问题:
  其中，$\mathcal{F}$ 是假设空间
  • e.g. 当模型是条件概率分布、损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计
    $$\begin{array}{rl}\underset{f\in \mathcal{F}}{\mathrm{argmin}}\frac{1}{N}\sum _{i=1}^{N}L(y_i,f(x_i))& =\underset{\theta }{\mathrm{argmin}}\frac{1}{N}\sum _{i=1}^N-\log P_{\theta }(y_i|x_i)\\ & =\underset{\theta }{\mathrm{argmax}}\log \prod _{i=1}^N{P}_{\theta }(y_i|x_i)\end{array}$$

---

结构风险最小化 (Structural risk minimization, SRM)

• 结构风险最小化是为了防止过拟合而提出来的策略。结构风险最小化等价于正则化 (regularization)。结构风险在经验风险上加上表示模型复杂度的正则化项 (regularizer) 或罚项 (penalty term) $J(f)$。结构风险的定义是:
  
  • 正则化符合奥卡姆剃刀 (Occam’s razor) 原理。奥卡姆剃刀原理应用于模型选择时变为以下想法: 在所有可能选择的模型中，能够很好地解释己知数据并且十分简单才是最好的模型
  • e.g. 当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计
    $$\begin{array}{rl}\underset{\theta }{\mathrm{argmax}}P(\theta |X)& =\underset{\theta }{\mathrm{argmax}}\log P(\theta |X)\\ & =\underset{\theta }{\mathrm{argmax}}\log \frac{P(X|\theta )P(\theta )}{P(X)}\\ & =\underset{\theta }{\mathrm{argmin}}-\log P(X|\theta )-\log P(\theta )\end{array}$$从贝叶斯估计的角度来看，正则化项对应于模型的先验概率。可以假设复杂的模型有较小的先验概率，简单的模型有较大的先验概率
• 正则化项可以取不同的形式
  • 例如，回归问题中，损失函数是平方损失，正则化项可以是参数向量的 L2 范数:
    正则化项也可以是参数向量的 L1 范数:
    

泛化误差上界 (generalization error bound)

• 学习方法的泛化能力分析往往是通过研究泛化误差的概率上界进行的。泛化误差上界通常具有以下性质:
  • 它是样本容量的函数，当样本容量增加时，泛化上界趋于 0
  • 它是假设空间容量 (capacity) 的函数，假设空间容量越大，模型就越难学，泛化误差上界就越大

---

定理 1.1 (泛化误差上界)

• 对二分类问题，当假设空间是有限个函数的集合 $\mathcal{F}=\{f_1,...,f_d\}$ 时，对任意一个函数 $f\in \mathcal{F}$， 至少以概率 $1-\delta ,0<\delta <1$，以下不等式成立:
  其中，$R(f)$ 为风险函数 $E[L(Y,f(X))]$，$\hat{R}(f)$ 为经验风险 $\frac{1}{N}{\sum }_{i=1}^{N}L(y_i,f(x_i))$
  

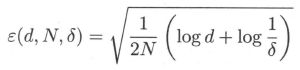
Hoeffding 不等式

• 在证明中要用到 Hoeffding 不等式 (证明省略): 设 $X_1,\dots ,X_N$ 是独立随机变量， 且 $X_i\in [a_i,b_i]$，$i=1,2,\dots ,N$; $\bar{X}=\frac{1}{N}{\sum }_{i=1}^N{X}_i$，则对任意 $t>0$，以下不等式成立:
  

证明

• 对任意函数 $f\in \mathcal{F}$，$\hat{R}(f)$ 是 $N$ 个独立的随机变量 $L(Y,f(X))$ 的样本均值，$R(f)$ 是随机变量 $L(Y,f(X))$ 的期望值。如果损失函数取值于区间 $[0,1]$，即对所有 $i$，$a_i=0,b_i=1$，那么由 Hoeffding 不等式不难得知，对 $\epsilon >0$，以下不等式成立:
  
• 由于 $\mathcal{F}=\{f_1,...,f_d\}$ 是一个有限集合，故
  即，对任意 $f\in \mathcal{F}$， 有
  
• 令
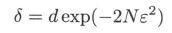  则
  

以上讨论的只是假设空间包含有限个函数情况下的泛化误差上界，对一般的假设空间要找到泛化误差界就没有这么简单，这里不作介绍

评估方法

“模型选择” (model selection)

• 理想的解决方案当然是对候选模型的泛化误差进行评估，然后选择泛化误差最小的那个模型. 然而如上面所讨论的，我们无法直接获得泛化误差，而训练误差又由于过拟合现象的存在而不适合作为标准，那么，在现实中如何进行模型评估与选择呢?

---

在现实任务中往往还会考虑时间开销、存储开销、可解释性等方面，这里暂且只考虑泛化误差

• 测试集 (testing set)：使用一个测试集来测试学习器对新样本的判别能力，然后以测试集上的 测试误差 (testing error) 作为泛化误差的近似
  • 测试样本也是从样本真实分布中独立同分布采样而得
  • 测试集应尽可能与训练集互斥，即测试样本尽量不在训练集中出现
• 我们可以通过对数据集 $D$ 进行适当的处理，从中产生出 训练集 $S$ 和 测试集 $T$. 下面介绍几种常见的做法

留出法 (hold-out)

• 直接将 $D$ 划分为两个互斥的集合 $S$ 和 $T$，在 $S$ 上训练出模型后，用 $T$ 来评估其测试误差，作为对泛化误差的估计
  • 另外，测试集小时，评估结果的方差较大， 训练集小时，评估结果的偏差较大；常见做法是将大约 $2/3$ ~ $4/5$ 的样本用于训练，剩余样本用于测试集 (一般而言，测试集至少应含 30 个样例)
• 需注意的是，训练 / 测试集的划分要尽可能保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响
  • 例如在分类任务中至少要保持样本的类别比例相似。如果从采样 (sampling) 的角度来看待数据集的划分过程，则保留类别比例的采样方式通常称为"分层采样" (stratified sampling)
• 另一个需注意的问题是，即使在给定训练/测试集的样本比例后，仍存在多种划分方式对初始数据集 $D$ 进行分割
  • 例如，可以把 $D$ 中的样本排序，然后把前 350 个正例放到训练集中，也可以把最后 350 个正例放到训练集中，…… 这些不同的划分将导致不同的训练 / 测试集，相应的，模型评估的结果也会有差别
  • 因此，单次使用留出法得到的估计结果往往不够稳定可靠，在使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果

交叉验证法 (cross validation)

• 交叉验证法 先将数据集 $D$ 划分为 $k$ 个大小相似的互斥子集. 每个子集 $D_i$ 都尽可能保持数据分布的一致性，即从 $D$ 中通过分层采样得到. 然后，每次用 $k-1$ 个子集的并集作为训练集，余下的那个子集作为测试集; 这样就可获得 $k$ 组 训练/测试集，从而可进行 $k$ 次训练和测试， 最终返回的是这 $k$ 个测试结果的均值.
• 显然，交叉验证法评估结果的稳定性和保真性在很大程度上取决于 $k$ 的取值，为强调这一点，通常把交叉验证法称为 $k$ 折交叉验证 ($k$-fold cross validation). $k$ 最常用的取值是 10
  
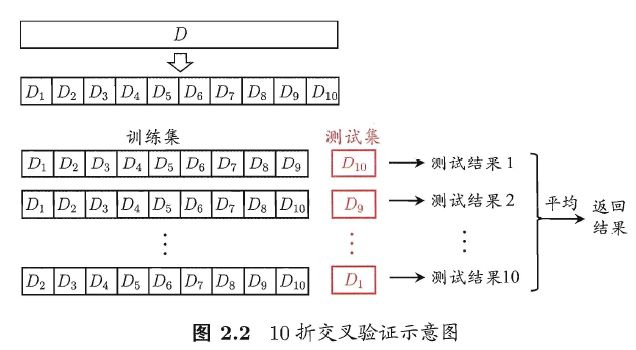
• 与留出法相似，将数据集 $D$ 划分为 $k$ 个子集同样存在多种划分方式. 为减小因样本划分不同而引入的差别， $k$ 折交叉验证通常要随机使用不同的划分重复 $p$ 次，最终的评估结果是这 $p$ 次 $k$ 折交叉验证结果的均值，例如常见的有 10 次 10 折交叉验证

---

留一法 (Leave-One-Out，简称 LOO)

• 假定数据集 $D$ 中包含 $m$ 个样本，若令 $k=m$， 则得到了交叉验证法的一个特例: 留一法. 显然， 留一法不受随机样本划分方式的影响
• 留一法使用的训练集与初始数据集相比只少了一个样本，这就使得在绝大多数情况下，留一法中被实际评估的模型与期望评估的用 $D$ 训练出的模型很相似. 因此，留一法的评估结果往往被认为比较准确.
• 然而，在数据集比较大时，训练 $m$ 个模型的计算开销可能是难以忍受的
• 另外，留一法的估计结果也未必永远比其他评估方法准确; "没有免费的午餐"定理对实验评估方法同样适用

自助法 (bootstrapping)

• 我们希望评估的是用 $D$ 训练出的模型. 但在留出法和交叉验证法中，实际评估的模型所使用的训练集比 $D$ 小，这必然会引入一些因训练样本规模不同而导致的估计偏差. 留一法受训练样本规模变化的影响较小，但计算复杂度又太高了.

---

• 自助法 是一个比较好的解决方案，它直接以 自助采样法 (bootstrap sampling) 为基础.
  • 给定包含 $m$ 个样本的数据集 $D$， 我们对它进行采样产生数据集 $D^{\prime }$: 每次随机从 $D$ 中挑选一个样本，将其拷贝放入 $D^{\prime }$，然后再将该样本放回初始数据集 $D$ 中，使得该样本在下次采样时仍有可能被采到; 这个过程重复执行 $m$ 次后，我们就得到了包含 $m$ 个样本的数据集 $D^{\prime }$.
  • 可以做一个简单的估计，样本在 $m$ 次采样中始终不被采到的概率是 $(1-\frac{1}{m}{)}^m$， 取极限得到 $li{m}_{m\to \infty }(1-\frac{1}{m}{)}^m=\frac{1}{e}\approx 0.368$. 即通过自助采样，初始数据集 $D$ 中约有 $36.8\%$ 的样本未出现在采样数据集 $D^{\prime }$ 中.于是我们可将 $D^{\prime }$ 用作训练集， $D-D^{\prime }$ 用作测试集; 这样，实际评估的模型与期望评估的模型都使用 $m$ 个训练样本，而我们仍有数据总量约 $1/3$ 的、没在训练集中出现的样本用于测试. 这样的测试结果，亦称 “包外估计” (out-of-bag estimate).
• 自助法在数据集较小、难以有效划分训练/测试集时很有用; 此外，自助法能从初始数据集中产生多个不同的训练集，这对集成学习等方法有很大的好处. (Bagging)
• 然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差. 因此，在初始数据量足够时，留出法和交叉验证法更常用一些

调参与最终模型

parameter tuning

“调参” (parameter tuning).

• 现实中常用的做法是对每个参数选定一个范围和变化步长，例如在 $[0,0.2]$ 范围内以 $0.05$ 为步长，则实际要评估的候选参数值有 5 个，最终是从这 5 个候选值中产生选定值. 显然，这样选定的参数值往往不是"最佳"值，但这是在计算开销和性能估计之间进行折中的结果
• 事实上，即便在进行这样的折中后，调参往往仍很困难.可以简单估算一下:假定算法有 3 个参数，每个参数仅考虑 5 个候选值，这样对每一组训练/测试集就有 $5^3=125$ 个模型需考察; 很多强大的学习算法有大量参数需设定，这将导致极大的调参工程量

---

最终模型

• 给定包含 $m$ 个样本的数据集 $D$，在模型评估与选择过程中由于需要留出一部分数据进行评估测试，事实上我们只使用了一部分数据训练模型. 因此，在模型选择完成后，学习算法和参数配置己选定，此时应该用数据集 $D$ 重新训练模型. 这个模型在训练过程中使用了所有 $m$ 个样本，这才是我们最终提交给用户的模型.

---

“验证集” (validation set)

• 需注意的是，我们通常把学得模型在实际使用中遇到的数据称为测试数据，为了加以区分，模型评估与选择中用于评估测试的数据集常称为"验证集" (validation set).
• 例如，在研究对比不同算法的泛化性能时，我们用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和验证集，基于验证集上的性能来进行模型选择和调参.

性能度量 (performance measure)

• 性能度量: 衡量模型泛化能力的评价标准

---

• 在预测任务中, 给定样例集 $D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...,({\mathbf{x}}_m,y_m)\}$
  • 回归任务最常用的性能度量是"均方误差" (mean squared error)
    更一般的，对于数据分布 $\mathcal{D}$ 和概率密度函数 $p(.)$， 均方误差可描述为
    

下面主要介绍分类任务中常用的性能度量.

错误率与精度 (Accuracy)

• 对样例集 $D$, 分类错误率定义为
  精度则定义为
  
• 更一般的，对于数据分布 $\mathcal{D}$ 和概率密度函数 $p(.)$， 错误率与精度可分别描述为
  

---

Accuracy 指标总是合适的吗？

• 考虑数据集样本类别分布不均衡的情况，例如数据集中 99% 是正类、1% 是负类，在这种情况下模型是只预测正类就能达到 99% 的 Accuracy，此时虽然 Accuracy 很高，但是意义不大。因此，对于不平衡数据集而言，Accuracy 并不是一个好指标
• 正因为 Accuracy 具有上述缺点，我们才需要进一步引入 Precision, Recall, F1-score, AUC 等指标

查准率 (precision)、查全率 / 召回率 (recall)、PR 曲线

查准率 与 查全率

• 对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例 (true positive) 、假正例 (false positive) 、真反例 (true negative) 、假反例 (false negative) 四种情形，令 $TP$、$FP$、$TN$、$FN$ 分别表示其对应的样例数. 分类结果的 "混淆矩阵" (confusion matrix) 如下表所示
  
• 查准率 $P$ 与查全率 $R$ 分别定义为
  查准率和查全率是一对矛盾的度量. 一般来说，查准率高时，查全率往往偏低; 而查全率高时，查准率往往偏低. 通常只有在一些简单任务中, 才可能使查全率和查准率都很高

---

P-R 曲线

• 在很多情形下，我们可根据学习器的预测结果对样例进行排序，排在前面的是学习器认为 “最可能” 是正例的样本. 按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率. 以查准率为纵轴、查全率为横轴作图，就得到了查准率-查全率曲线，简称 “P-R 曲线”
  

为绘图方便和美观，示意图显示出单调平滑曲线，但现实任务中的 P-R 曲线常是非单调、不平滑的，在很多局部有上下波动

• 在进行比较时，若一个学习器的 P-R 曲线被另一个学习器的曲线完全"包住" ， 则可断言后者的性能优于前者，例如上图中学习器 $A$ 的性能优于学习器 $C$
• 如果两个学习器的 P-R 曲线发生了交叉, 例如上图中的 $A$ 与 $B$ ，则难以一般性地断言两者孰优孰劣。只能在具体的查准率或查全率条件下进行比较. 然而，在很多情形下，人们往往仍希望把学习器 $A$ 与 $B$ 比出个高低. 这时一个比较合理的判据是比较 P-R 曲线下面积的大小，但这个值不太容易估算， 因此，人们设计了一些综合考虑查准率、查全率的性能度量.
  • “平衡点” (Break-Event Point，BEP) 就是这样一个度量，它是 “查准率 $=$ 查全率” 时的取值
    • 例如上图中学习器 $C$ 的 BEP 是 $0.64$，而基于 BEP 的比较，可认为学习器 $A$ 优于 $B$
  • 但 BEP 还是过于简化了些，更常用的是 $F1$ 度量:
    $F1$ 是基于查准率与查全率的调和平均 (harmonic mean) 定义的:
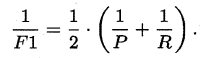    与算术平均 ($(P+R)/2$) 和几何平均 $(\sqrt{PR})$ 相比，调和平均更重视较小值
  • 在一些应用中，对查准率和查全率的重视程度有所不同. 例如在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确是用户感兴趣的，此时查准率更重要;而在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时查全率更重要. $F_1$ 度量的一般形式–$F_{\beta }$ 能让我们表达出对查准率/查全率的不同偏好
    
    • $F_{\beta }$ 是基于查准率与查全率的加权调和平均定义的:
      其中 $\beta >0$ 度量了查全率对查准率的相对重要性. $\beta =1$ 时退化为标准的 $F_1$; $\beta >1$ 时查全率有更大影响; $\beta <1$ 时查准率有更大影响.

---

二分类 $\to$ 多分类

• 很多时候我们有多个二分类混淆矩阵，例如进行多次训练/测试，每次得到一个混淆矩阵;或是在多个数据集上进行训练/测试，希望估计算法的"全局"性能;甚或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵，总之，我们希望在 $n$ 个二分类混淆矩阵上综合考察查准率和查全率
• (1) Macro-average: 一种直接的做法是先在各混淆矩阵上分别计算出查准率和查全率， 再计算平均值，这样就得到 “宏查准率” (macro-P) 、“宏查全率” (macro-R) ，以及相应的 “宏 F1” (macro-F1)。该方法能够平等看待每个类别，但是它的值会受稀有类别影响
  注意到，这里 macro-F1 仍为 macro-P 和 macro-R 的调和平均，它的值应该是介于 macro-P 和 macro-R 之间的。但在 sklearn 的实现中，macro-F1 却是由不同类别的 F1 取平均得到的，并不为 macro-P 和 macro-R 的调和平均，它的取值也就不一定在 macro-P 和 macro-R 之间了
• (2) Weighted-average: 与 Macro-average 相比，不再是单纯地计算平均值，而是给不同类别不同权重 (权重根据该类别的真实分布比例确定)，每个类别乘权重后再进行相加。该方法考虑了类别不平衡情况，它的值更容易受到常见类 (majority class) 的影响
• (3) Micro-average: 还可先将各混淆矩阵的对应元素进行平均，得到 TP、FP、TN、FN 的平均值, 再基于这些平均值计算出 “微查准率" (micro-P)”、“ 微查全率" (micro-R) 和“ 微 F1" (micro-F1):
  其中，特别有意思的是，Micro-precision 和 Micro-recall 其实是一样的！把上式中的平均符号都改为求和号，可以看到 Micro-precision 和 Micro-recall 只有分母上的 ${\sum }_{i=1}^{C}F{P}_i$ 和 ${\sum }_{i=1}^{C}F{N}_i$ 不同，而对于一个类别的 FP 样本而言，它一定是另一个类别的 FN 样本，因此 ${\sum }_{i=1}^{C}F{P}_i={\sum }_{i=1}^{C}F{N}_i$，也就有 Micro-precision = Micro-recall，并且它们都等于分类正确的样本数除以总样本数，也就是 Accuracy：

ROC 与 AUC

参考：模型评估与选择（中篇）- ROC 曲线与 AUC 曲线

Why ROC? (Receiver Operating Characteristic)

• 很多学习器是为测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阙值 (threshold) 进行比较，若大于阙值则分为正类，否则为反类．根据这个实值或概率预测结果，我们可将测试样本进行排序， “最可能” 是正例的排在最前面，“最不可能” 是正例的排在最后面． 这样，分类过程就相当于在这个排序中以某个“截断点" (cut point) 将样本分为两部分，前一部分判作正例，后一部分则判作反例
  • 在不同的应用任务中，我们可根据任务需求来采用不同的截断点，例如若我们更重视“查准率” ，则可选择排序中靠前的位置进行截断； 若更重视“查全率” ，则可选择靠后的位置进行截断
• 因此排序本身的质量好坏，体现了综合考虑学习器在不同任务下的” 期望泛化性能” 的好坏. ROC 曲线则是从这个角度出发来研究学习器泛化性能的有力工具 (ROC 曲线独立于阈值，也独立于样本的分布，只与排序质量有关)

---

怎么画 ROC

• ROC 全称是“ 受试者工作特征" 曲线. 与 P-R 曲线相似，我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了 “ROC曲线”. ROC 曲线的纵轴是“真正例率" (True Positive Rate, 简称TPR), 横轴是“假正例率" (False Positive Rate, 简称 FPR)
  
  • 对角线对应于"随机猜测" 模型 ($\frac{TP}{FP}=\frac{m^{+}}{m^{-}}$)，而点 $(0，1)$ 则对应于将所有正例排在所有反例之前的"理想模型"；在对角线以上的点属于比较好的模型，在对角线以下的模型实际上就跟反向预测一样了…
  • 一般来说，TPR 和 FPR 相互制约；例如某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病, 那么 TPR 应该会很高, 但是 FPR 也会相应地变高。最极端的情况下, 他把所有的样本都看做有病, 那么 TPR 达到 1, FPR 也为 1
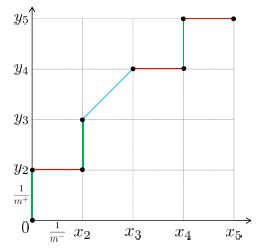
• 现实任务中通常是利用有限个测试样例来绘制 ROC 图，此时仅能获得有限个坐标对，无法产生光滑 ROC 曲线， 只能绘制出近似 ROC 曲线. 绘图过程很简单:
  • 给定 $m^{+}$ 个正例和 $m^{-}$ 个反例，根据学习器预测结果对样例进行排序，然后把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为 0， 在坐标 $(0，0)$ 处标记一个点; 然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划分为正例. 设前一个标记点坐标为 $(x,y)$，当前若为真正例，则对应标记点的坐标为 $(x,y+\frac{1}{m^{+}})$; 当前若为假正例，则对应标记点的坐标为 $(x+\frac{1}{m^{-}},y)$，然后用线段连接相邻点即得.
    

---

AUC

• 进行学习器的比较时， 与 P-R 图相似， 若一个学习器的 ROC 曲线被另一个学习器的曲线完全"包住"， 则可断言后者的性能优于前者; 若两个学习器的 ROC 曲线发生交叉，则难以一般性地断言两者孰优孰劣. 此时如果一定要进行比较， 则较为合理的判据是比较 ROC 曲线下的面积，即 AUC (Area Under ROC Curve) . 假定 ROC 曲线是由坐标为 $\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$ 的点按序连接而形成 ($x_1=0,x_m=1$), 则 AUC 可估算为
  
  • 解析：如下图所示，$x$ 轴（假正例率轴）的单位刻度为 $\frac{1}{m^{-}}$, $y$ 轴（真正例率轴）的单位刻度定为 $\frac{1}{m^{+}}$. 绿色线段表示在分类阈值变动的过程中只新增了真正例，红色线段表示只新增了假正例，蓝色线段表示既新增了真正例也新增了假正例。此时的 AUC 值其实就是所有红色线段和蓝色线段与 $x$ 轴围成的面积之和
  • 观察下图可知，红色线段与 $x$ 轴围成的图形恒为矩形，蓝色线段与 $x$ 轴围成的图形恒为梯形，但是由于梯形面积公式既能算梯形面积，也能算矩形面积，所以无论是红色线段还是蓝色线段，其与 $x$ 轴围成的面积都能用梯形公式来计算，也即 $\frac{1}{2}\cdot \left(x_{i+1}-x_i\right)\cdot \left(y_i+y_{i+1}\right)$
    
• 显然, AUC 越大, 分类器分类效果越好
  • AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测
  • 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值
  • AUC = 0.5，跟随机猜测一样，模型没有预测价值
  • AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测

---

AUC 与 排序损失

• 形式化地看，AUC 考虑的是样本预测的排序质量，因此它与排序误差有紧密联系. 给定 $m^{+}$ 个正例和 $m^{-}$ 个反例, 令 $D^{+}$ 和 $D^{-}$ 分别表示正、 反例集合，则排序 “损失" (loss)定义为
  即考虑每一对正、 反例，若正例的预测值小于反例则记一个 “罚分” ，若相等则记 0.5 个 “罚分”．容易看出，${\ell }_{rank}$ 对应的是 ROC 曲线之上的面积 (所有绿色线段和蓝色线段与 $y$ 轴围成的面积之和)，因此有
  
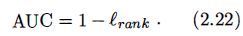
  • 解析：首先对式 (2.21) 进行变形：
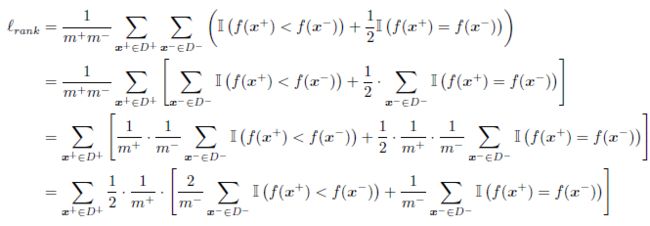    根据公式 (2.20) 中给出的 ROC 曲线图可知，在变动分类阈值的过程当中，如果有新增真正例，那么相应地就会增加一条绿色线段或蓝色线段，所以上式中的 ${\sum }_{x^{+}\in D^{+}}$ 可以看作是在遍历所有绿色和蓝色线段，那么相应地 ${\sum }_{x^{+}\in D^{+}}$ 后面的那一项便是在求绿色线段或者蓝色线段与 $y$ 轴围成的面积，也即
    上式表示的依旧是一个梯形的面积求解公式。其中 $\frac{1}{m^{+}}$ 即为梯形的“高”，“上底” 为绿色或者蓝色线段的下端点到 $y$ 轴的距离，即
    而下底为
    
• 因此，如前所述，ROC 独立于阈值，也独立于样本的分布，只与排序质量有关
  • 例如，当测试集中的正负样本的分布变换的时候，ROC 曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡，即正负样本比例差距较大，而且测试数据中的正负样本也可能随着时间变化。下图是 ROC 曲线和 Presision-Recall 曲线的对比 ((a) 和 ($c$) 为 ROC 曲线，(b) 和 (d) 为 Precision-Recall 曲线)：
    (a) 和 (b) 展示的是分类其在原始测试集 (正负样本分布平衡) 的结果，($c$) (d) 是将测试集中负样本的数量增加到原来的 10 倍后，分类器的结果，可以明显的看出，ROC 曲线基本保持原貌，而 Precision-Recall 曲线变化较大

代价敏感错误率与代价曲线

• 在现实任务中常会遇到这样的清况：不同类型的错误所造成的后果不同
  • 例如在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者，看起来都是犯了 “一次错误”，但后者的影响是增加了进一步检查的麻烦，前者的后果却可能是丧失了拯救生命的最佳时机
• 为权衡不同类型错误所造成的不同损失，可为错误赋予 “非均等代价"(unequal cost).

---

代价矩阵 (cost matrix)

• 以二分类任务为例，我们可根据任务的领域知识设定一个 代价矩阵 (cost matrix), 如表 2.2 所示 ，其中 $cos{t}_{ij}$ 表示将第 $i$ 类样本预测为第 $j$ 类样本的代价. 一般来说 $cos{t}_{ii}=0$; 若将第 0 类判别为第 1 类所造成的损失更大，则 $cos{t}_{01}>cos{t}_{10}$; 一般情况下，重要的是代价比值而非绝对值， 例如 $cos{t}_{01}:cos{t}_{10}=5:1$ 与 $50:10$ 所起效果相当
  

---

“代价敏感” (cost-sensitive) 错误率

• 令 $D^{+}$ 与 $D^{-}$ 分别代表样例集 $D$ 的正例子集和反例子集，则 “代价敏感” (cost-sensitive) 错误率为
  类似的，可给出基于分布定义的代价敏感错误率，以及其他一些性能度量如精度的代价敏感版
• 若令 $cos{t}_{ij}$ 中的 $i$、$j$ 取值不限于 0 、1 ，则可定义出多分类任务的代价敏感性能度量

---

“代价曲线” (cost curve)

• 在非均等代价下， ROC 曲线不能直接反映出学习器的期望总体代价，而 “代价曲线” 则可达到该目的
• 代价曲线图的横轴是取值为 $[0,1]$ 的正例概率代价
  其中 $p$ 是样例为正例的概率; 纵轴是取值为 $[0,1]$ 的归一化代价
  其中 FPR 是式 (2.19) 定义的假正例率，FNR = 1 - TPR 是假反例率
• 代价曲线的绘制很简单： ROC 曲线上每一点对应了代价平面上的 一条线段，设 ROC 曲线上点的坐标为 (TPR, FPR), 则可相应计算出 FNR, 然后在代价平面上绘制一条从 (0, FPR) 到 (1, FNR) 的线段，线段下的面积即表示了该条件下的期望总体代价；如此将 ROC 曲线上的每个点转化为代价平面上的一条线段，然后取所有线段的下界，围成的面积即为在所有条件下学习器的期望总体代价，如图 2.5 所示．
  

详细介绍可参考 模型评估与选择（后篇）- 代价曲线

Discounted Cumulative Gain (DCG)

• ref: Discounted Cumulative Gain

---

• DCG 是衡量排序质量的一种测度。在信息检索中，DCG 通常用于衡量网络搜索引擎的有效性

Cumulative Gain (CG)

• 对于 $p$ 个搜索结果，排序位置 $p$ 的 Cumulative Gain 为
  $$C{G}_p=\sum _{i=1}^{p}re{l}_i$$其中，$re{l}_i$ 为排序位置 $i$ 的搜索结果与搜索内容的相关性得分
• 从上式可以看出，CG 不受搜索结果排序方式的影响

Discounted cumulative gain (DCG)

• 为了把搜索结果的排序方式也纳入评价标准，DCG 根据搜索结果所在的位置对其相关性得分进行打折：
  $$DC{G}_p=\sum _{i=1}^p\frac{re{l}_i}{{\log }_2(i+1)}={rel}_1+\sum _{i=2}^p\frac{re{l}_i}{{\log }_2(i+1)}$$DCG 还有如下的替换形式 (places stronger emphasis on retrieving relevant documents)：
  $$DC{G}_p=\sum _{i=1}^p\frac{2^{re{l}_i}-1}{{\log }_2(i+1)}$$

Normalized DCG (nDCG)

• nDCG 为
  $$nDC{G}_p=\frac{DC{G}_p}{IDC{G}_p}\in [0,1]$$其中，$IDC{G}_p$ 为 Ideal DCG (IDCG)，即将搜索结果按相关性得分降序排序后计算得到的可能的最大 DCG
  $$IDC{G}_p=\sum _{i=1}^{|REL|}\frac{2^{re{l}_i}-1}{{\log }_2(i+1)}$$
• 通过归一化，我们就能很方便地比较出搜索结果数量不同的 result list 之间的排序质量

偏差与方差

偏差-方差分解

• “偏差-方差分解” (bias-variance decomposition) 是解释学习算法泛化性能的一种重要工具. 偏差方差分解试图对学习算法的期望泛化错误率进行拆解

---

• 我们知道，算法在不同训练集上学得的结果很可能不同，即便这些训练集是来自同一个分布. 对测试样本 $x$, 令 $y_D$ 为 $x$ 在数据集中的标记，$y$ 为 $x$ 的真实标记，$f(x;D)$ 为训练集 $D$ 上学得模型 $f$ 在 $x$ 上的预测输出 (有可能出现噪声使得 $y_D\ne y$)
• 以回归任务为例，对于样本 $x$, 学习算法的期望预测为
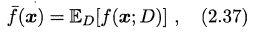  使用样本数相同的不同训练集产生的方差为
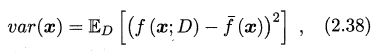  噪声为
  期望输出与真实标记的差别称为偏差 (bias) ，即
  
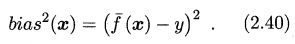
• 为便于讨论，假定噪声期望为 0，即 ${\mathbb{E}}_D[y_D-y]=0$. 通过简单的多项式展开合并，可对算法的期望泛化误差进行分解:
  $$\begin{array}{rl}E(f;D)=& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[{\left(f(\mathbf{x};D)-\bar{f}(\mathbf{x})+\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[(f(\mathbf{x};D)-\bar{f}(\mathbf{x}){)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ & +{\mathbb{E}}_D\left[2(f(\mathbf{x};D)-\bar{f}(\mathbf{x}))\left(\bar{f}(\mathbf{x})-y_D\right)\right]\end{array}$$其中，
  $$\begin{array}{rl}& {\mathbb{E}}_D\left[2(f(\mathbf{x};D)-\bar{f}(\mathbf{x}))\left(\bar{f}(\mathbf{x})-y_D\right)\right]\\ =& {\mathbb{E}}_D[2(f(\mathbf{x};D)-\bar{f}(\mathbf{x}))\cdot \bar{f}(\mathbf{x})]-{\mathbb{E}}_D\left[2(f(\mathbf{x};D)-\bar{f}(\mathbf{x}))\cdot y_D\right]\\ =& 2\bar{f}(\mathbf{x}){\mathbb{E}}_D[f(\mathbf{x};D)-\bar{f}(\mathbf{x})]-2{\mathbb{E}}_D\left[f(\mathbf{x};D)\cdot y_D-\bar{f}(\mathbf{x})\cdot y_D\right]\\ =& 0-2{\mathbb{E}}_D\left[f(\mathbf{x};D)\cdot y_D\right]+2{\mathbb{E}}_D\left[\bar{f}(\mathbf{x})\cdot y_D\right]\\ =& -2\bar{f}(\mathbf{x})\cdot {\mathbb{E}}_D\left[y_D\right]+2\bar{f}(\mathbf{x}){\mathbb{E}}_D\left[y_D\right]\\ =& 0\end{array}$$因此有
  $$\begin{array}{rl}E(f;D)=& {\mathbb{E}}_D\left[(f(\mathbf{x};D)-\bar{f}(\mathbf{x}){)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[(f(\mathbf{x};D)-\bar{f}(\mathbf{x}){)}^2\right]+{\mathbb{E}}_D\left[{\left(\bar{f}(\mathbf{x})-y+y-y_D\right)}^2\right]\\ =& {\mathbb{E}}_D\left[(f(\mathbf{x};D)-\bar{f}(\mathbf{x}){)}^2\right]+{\mathbb{E}}_D\left[(\bar{f}(\mathbf{x})-y{)}^2\right]+{\mathbb{E}}_D\left[{\left(y-y_D\right)}^2\right]\\ & +2{\mathbb{E}}_D\left[(\bar{f}(\mathbf{x})-y)\left(y-y_D\right)\right]\\ =& {\mathbb{E}}_D\left[(f(\mathbf{x};D)-\bar{f}(\mathbf{x}){)}^2\right]+(\bar{f}(\mathbf{x})-y{)}^2+{\mathbb{E}}_D\left[{\left(y_D-y\right)}^2\right]\\ & (2.41)\end{array}$$
• 于是，
  也就是说, 泛化误差可分解为偏差、方差与噪声之和.
  • 偏差 (2.40) 度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力
  • 方差 (2.38) 度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响
  • 噪声 (2.39) 则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度
• 偏差-方差分解说明，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的. 给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小.

偏差-方差窘境 (bias-variance dilemma)

• 给定学习任务，假定我们能控制学习算法的训练程度，则在训练不足时学习器的拟合能力不够强，训练数据的扰动不足以便学习器产生显著变化，此时偏差主导了泛化错误率; 随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率; 在训练程度充足后，学习器的拟合能力已非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则将发生过拟合
  

参考文献

• 《机器学习》(周志华)、南瓜书
• 《统计学习方法》(李航) 的读书笔记
• 多分类模型 Accuracy, Precision, Recall 和 F1-score 的超级无敌深入探讨
• 机器学习中 macro-F1 的计算公式？