图解LeetCode搜索旋转排序数组问题
今天有人问我LeetCode第33题:搜索旋转排序数组,这就是我想到的解法。
为了下文简化描述,我们定义这几个概念:
- 左节点(左):当前迭代序列的左节点,下标
il - 右节点(右):当前迭代序列的右节点,下标
ir - 中位点(中):当前迭代序列的中位点,下标
(il + ir) / 2 - 断点(断):升序数组的最大点
- 目标节点(标):待搜索的节点
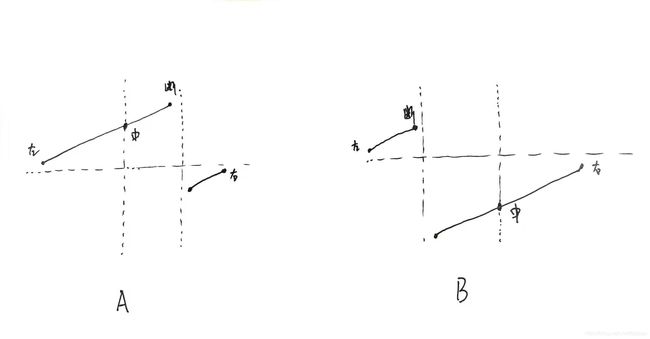
题目要求必须是O(logn)级别,因此必须使用二分查找。假如数组没有旋转,就转化为二分查找了,那就很简单了,也不是题目的考察目标,因此我们只考虑一个升序数组做了一次旋转的情况。下面这张图很重要,本文的分析都基于这张图:
下面请一步一步的跟着我的分析思路:
【1】 因为存在断点,所以左节点一定在坐标轴的上半部分,右节点一定在坐标轴的下半部分,因此:
左节点 > 右节点
也即:
右节点 < 左节点
【2】 针对图中左侧的A情况,中位点位于左节点、断点之间,所以必然存在:
左节点 < 中位点
右节点 < 左节点
也即:
右节点 < 左节点 < 中位点
此时,目标点可能位于左节点与中位点之间【3】、中位点与断点之间【4】、断点与右节点之间【5】
【3】 针对情况A,目标点位于左节点与中位点之间:
左节点 < 目标节点 < 中位点
右节点 < 左节点 < 中位点
也即:
右节点 < 左节点 < 目标节点 < 中位点,简称:右左标中,应该向前查询
【4】 针对情况A,目标点位于中位点与断点之间:
中位点 < 目标节点
右节点 < 左节点 < 中位点
也即:
右节点 < 左节点 < 中位点 < 目标节点,简称:右左中标,应该向后查询
【5】 针对情况A,目标点位于断点与右节点之间:
目标节点 < 右节点
右节点 < 左节点 < 中位点
也即:
目标节点 < 右节点 < 左节点 < 中位点,简称:标右左中,应该向后查询
【6】针对图中右侧的情况B,中位点位于断点、右节点之间,所以必然存在:
中位点 < 右节点
右节点 < 左节点
也即:
中位点 < 右节点 < 左节点
此时,目标点可能位于左节点与断点之间【7】、断点与中位点之间【8】、中位点与右节点之间【9】
【7】 针对情况B,目标点位于左节点与断点之间:
左节点 < 目标节点
中位点 < 右节点 < 左节点
也即:
中位点 < 右节点 < 左节点 < 目标节点,简称:中右左标,应该向前查询
【8】 针对情况B,目标点位于断点与中位点之间:
目标节点 < 中位点
中位点 < 右节点 < 左节点
也即:
目标节点 < 中位点 < 右节点 < 左节点,简称:标中右左,应该向前查询
【9】针对情况B,目标点位于中位点与右节点之间:
中位点 < 目标节点 < 右节点
中位点 < 右节点 < 左节点
也即:
中位点 < 目标节点 < 右节点 < 左节点,简称:中标右左,应该向后查询
综上,只需要比较左节点、右节点、中位点、目标节点四者之间的关系,就可以知道应该向前查询还是向后查询了:
| 从小到大 | 处理 |
|---|---|
| 右左标中 | 应该向前查询 |
| 右左中标 | 应该向后查询 |
| 标右左中 | 应该向后查询 |
| 中右左标 | 应该向前查询 |
| 标中右左 | 应该向前查询 |
| 中标右左 | 应该向后查询 |
| 其他 | 找到了或不存在 |
代码实现如下:
package _033_search_in_rotated_sorted_array
const (
rltm = iota // 右左标中 应该向前查询
rlmt // 右左中标 应该向后查询
trlm // 标右左中 应该向后查询
mrlt // 中右左标 应该向前查询
tmrl // 标中右左 应该向前查询
mtrl // 中标右左 应该向后查询
)
func _state(nums []int, il, ir, im, target int) int {
switch {
case nums[ir] < nums[il] && nums[il] < target && target < nums[im]:
return rltm
case nums[ir] < nums[il] && nums[il] < nums[im] && nums[im] < target:
return rlmt
case target < nums[ir] && nums[ir] < nums[il] && nums[il] < nums[im]:
return trlm
case nums[im] < nums[ir] && nums[ir] < nums[il] && nums[il] < target:
return mrlt
case target < nums[im] && nums[im] < nums[ir] && nums[ir] < nums[il]:
return tmrl
case nums[im] < target && target < nums[ir] && nums[ir] < nums[il]:
return mtrl
default:
return -1
}
}
func _search(nums []int, il, ir, target int) (index int) {
// 异常下标
if 0 > il || ir >= len(nums) || il > ir {
return -1
}
if nums[il] == target {
return il
} else if nums[ir] == target {
return ir
} else if il+1 == ir {
// 既不等于左,也不等于右,中间也没别的数据了 肯定找不到
return -1
}
im := (il + ir) / 2
if nums[im] == target {
return im
}
if nums[il] < nums[ir] {
// 数组没有旋转
if target < nums[im] {
return _search(nums, il, im, target)
} else {
return _search(nums, im, ir, target)
}
} else if nums[il] == nums[ir] {
// 题目应该不会出现这种情况
return -1
}
switch _state(nums, il, ir, im, target) {
case rltm, mrlt, tmrl:
return _search(nums, il, im, target)
case rlmt, trlm, mtrl:
return _search(nums, im, ir, target)
default:
return -1
}
}
func search(nums []int, target int) int {
return _search(nums, 0, len(nums)-1, target)
}