神经网络与深度学习day09-卷积神经网络2：基础算子

5.2 卷积神经网络的基础算子

我们先实现卷积网络的两个基础算子：卷积层算子和汇聚层算子。

5.2.1 卷积算子

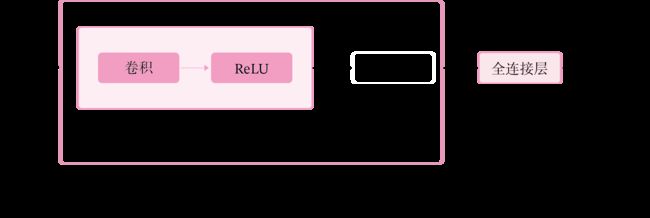
卷积层是指用卷积操作来实现神经网络中一层。

为了提取不同种类的特征，通常会使用多个卷积核一起进行特征提取。

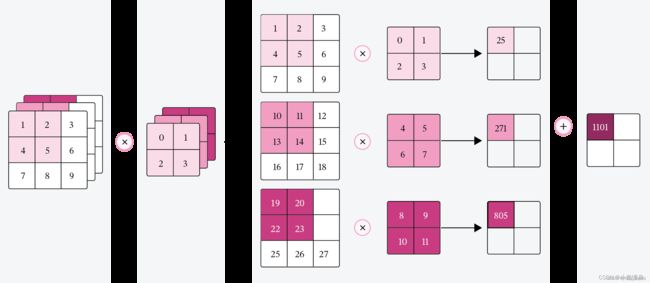
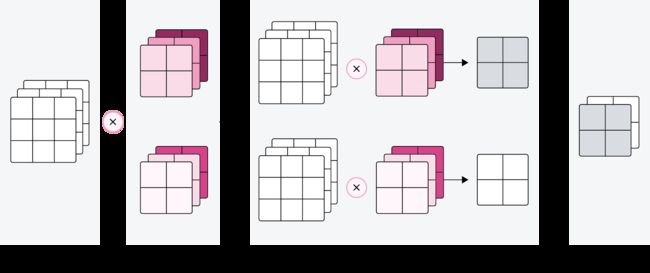
5.2.1.1 多通道卷积

5.2.1.2 多通道卷积层算子

1. 多通道卷积卷积层的代码实现

2. Pytorch：torch.nn.Conv2d()代码实现

3. 比较自定义算子和框架中的算子

代码实现：

import torch
import torch.nn as nn
class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,weight_attr=[],bias_attr=[]):
        super(Conv2D, self).__init__()
        # 创建卷积核
        weight_attr = torch.randn([out_channels, in_channels, kernel_size,kernel_size])
        weight_attr = torch.nn.init.constant(torch.tensor(weight_attr,dtype=torch.float32),val=1.0)
        self.weight = torch.nn.Parameter(weight_attr)
        # 创建偏置
        bias_attr = torch.zeros([out_channels, 1])
        bias_attr = torch.tensor(bias_attr,dtype=torch.float32)
        self.bias = torch.nn.Parameter(bias_attr)
        self.stride = stride
        self.padding = padding
        # 输入通道数
        self.in_channels = in_channels
        # 输出通道数
        self.out_channels = out_channels

    # 基础卷积运算
    def single_forward(self, X, weight):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
        new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
        u, v = weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*weight, 
                    axis=[1,2])
        return output

    def forward(self, inputs):
        """
        输入：
            - inputs：输入矩阵，shape=[B, D, M, N]
            - weights：P组二维卷积核，shape=[P, D, U, V]
            - bias：P个偏置，shape=[P, 1]
        """
        feature_maps = []
        # 进行多次多输入通道卷积运算
        p=0
        for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
            multi_outs = []
            # 循环计算每个输入特征图对应的卷积结果
            for i in range(self.in_channels):
                single = self.single_forward(inputs[:,i,:,:], w[i])
                multi_outs.append(single)
                # print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
            # 将所有卷积结果相加
            feature_map = torch.sum(torch.stack(multi_outs), axis=0) + b #Zp
            feature_maps.append(feature_map)
            # print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
            p+=1
        # 将所有Zp进行堆叠
        out = torch.stack(feature_maps, 1) 
        return out

inputs = torch.tensor([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv2d = Conv2D(in_channels=2, out_channels=3, kernel_size=2)
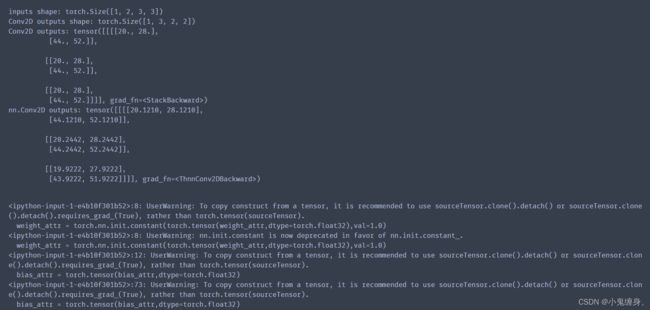
print("inputs shape:",inputs.shape)
outputs = conv2d(inputs)
print("Conv2D outputs shape:",outputs.shape)

# 比较与torch API运算结果
weight_attr = torch.ones([3,2,2,2])
bias_attr = torch.zeros([3, 1])
bias_attr = torch.tensor(bias_attr,dtype=torch.float32)
conv2d_torch = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=2,bias=True)
conv2d_torch.weight = torch.nn.Parameter(weight_attr)
outputs_torch = conv2d_torch(inputs)
# 自定义算子运算结果
print('Conv2D outputs:', outputs)
# torch API运算结果
print('nn.Conv2D outputs:', outputs_torch)

实现效果：

5.2.1.3 卷积算子的参数量和计算量

随着隐藏层神经元数量的变多以及层数的加深，

使用全连接前馈网络处理图像数据时，参数量会急剧增加。

如果使用卷积进行图像处理，相较于全连接前馈网络，参数量少了非常多。
因为没有一个统一的标准来比较全连接前馈网络和卷积网络的参数量和计算量，所以这里我们只提出一层二维卷积的参数量和计算量来体现一下：
参数量
我们使用的卷积核大小为[KS，KS]
其参数量为：$$KS\ast KS+1$$
若考虑输入和输出通道，则产生的参数量为：$$(C_{in}\ast (KS\ast KS)+1)\ast C_{out}$$
其中，$$C_{in}$$为输入通道大小，$$C_{out}$$为输出通道大小。
计算量
我们使用的卷积核大小为[KS，KS]
输入图的大小为：$$(H_{in},W_{in})$$，输出图的大小为：$$(H_{out},W_{out})$$
若考虑输入和输出通道：$$C_{in}\ast KS\ast KS\ast H_{out}\ast W_{out}\ast C_{out}$$
参考博客：卷积中参数量和计算量

5.2.2 汇聚层算子

汇聚层的作用是进行特征选择，降低特征数量，从而减少参数数量。

由于汇聚之后特征图会变得更小，如果后面连接的是全连接层，可以有效地减小神经元的个数，节省存储空间并提高计算效率。

常用的汇聚方法有两种，分别是：平均汇聚、最大汇聚。

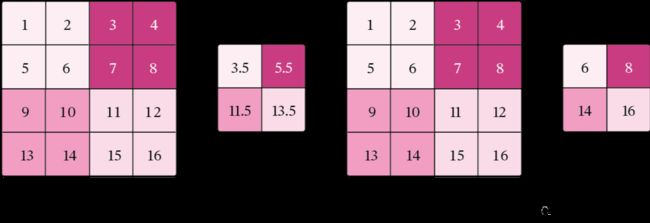
1. 代码实现一个简单的汇聚层。

2. torch.nn.MaxPool2d() ;torch.nn.avg_pool2d() 代码实现

3. 比较自定义算子和框架中的算子

代码实现：

class Pool2D(nn.Module):
    def __init__(self, size=(2,2), mode='max', stride=1):
        super(Pool2D, self).__init__()
        # 汇聚方式
        self.mode = mode
        self.h, self.w = size
        self.stride = stride

    def forward(self, x):
        output_w = (x.shape[2] - self.w) // self.stride + 1
        output_h = (x.shape[3] - self.h) // self.stride + 1
        output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
        # 汇聚
        for i in range(output.shape[2]):
            for j in range(output.shape[3]):
                # 最大汇聚
                if self.mode == 'max':
                    value_m = max(torch.max(x[:, :, self.stride*i:self.stride*i+self.w, self.stride*j:self.stride*j+self.h], 
                                            axis=3).values[0][0])
                    output[:, :, i, j] = torch.tensor(value_m)
                # 平均汇聚
                elif self.mode == 'avg':
                    value_m = max(torch.mean(x[:, :, self.stride*i:self.stride*i+self.w, self.stride*j:self.stride*j+self.h], 
                        axis=3)[0][0])
                    output[:, :, i, j] = torch.tensor(value_m)
        
        return output
#1.实现一个简单汇聚层
inputs = torch.tensor([[[[1.,2.,3.,4.],[5.,6.,7.,8.],[9.,10.,11.,12.],[13.,14.,15.,16.]]]])
pool2d = Pool2D(stride=2)
outputs = pool2d(inputs)
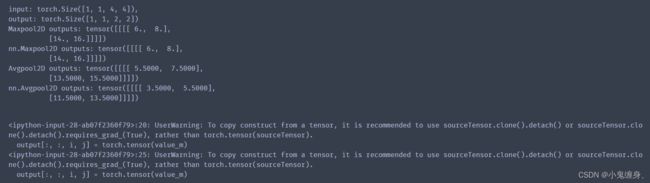
print("input: {}, \noutput: {}".format(inputs.shape, outputs.shape))
# 2.自定义算子上述代码已经实现，下面我们进行比较。
# 3.比较Maxpool2D与torch API运算结果
maxpool2d_torch = nn.MaxPool2d(kernel_size=(2,2), stride=2)
outputs_torch = maxpool2d_torch(inputs)
# 自定义算子运算结果
print('Maxpool2D outputs:', outputs)
# torch API运算结果
print('nn.Maxpool2D outputs:', outputs_torch)

# 3.比较Avgpool2D与torch API运算结果
avgpool2d_torch = nn.AvgPool2d(kernel_size=(2,2), stride=2)
outputs_torch = avgpool2d_torch(inputs)
pool2d = Pool2D(mode='avg', stride=2)
outputs = pool2d(inputs)
# 自定义算子运算结果
print('Avgpool2D outputs:', outputs)
# torch API运算结果
print('nn.Avgpool2D outputs:', outputs_torch)

结果：

汇聚层的参数量和计算量

• 由于汇聚层中没有参数，所以参数量为0；
• 最大汇聚中，没有乘加运算，所以计算量为0，
• 平均汇聚中，输出特征图上每个点都对应了一次求平均运算。

选做题：使用pytorch实现Convolution Demo

1.翻译以下内容

翻译：卷积演示：下面是一个正在运行的卷积层的示例，因为3D体积很难去可视化，所有的体积(输入体积(蓝色)，权重体积(红色)，输出体积(绿色))和每个深度层堆叠成行被可视化。输入体积是W1=5,H1=5,D1=3大小的，并且卷积层的参数是K=2,F=3,S=2,P=1。就是说，我们有两个大小为3*3的卷积核(滤波器)，并且他们的步长为2，因此，输出体积大小有空间大小为：(5-3+2)/2 +1 =3。除此之外，注意到padding(填充)的P=1被应用于输入体积，使得输入体积的外部边界为0。下面的可视化迭代输出激活(绿色)，并且展示了每个元素的计算方法是将高亮的输入(蓝色)与过滤器(红色)逐个元素相乘，然后相加，用偏差抵消结果。

2.代码实现下图

我们使用之前定义的Conv2D算子进行实现，自写代码如下：

import torch
import torch.nn as nn
class Conv2D(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,weight_attr=[],bias_attr=[]):
        super(Conv2D, self).__init__()
        self.weight = torch.nn.Parameter(weight_attr)
        self.bias = torch.nn.Parameter(bias_attr)
        self.stride = stride
        self.padding = padding
        # 输入通道数
        self.in_channels = in_channels
        # 输出通道数
        self.out_channels = out_channels

    # 基础卷积运算
    def single_forward(self, X, weight):
        # 零填充
        new_X = torch.zeros([X.shape[0], X.shape[1]+2*self.padding, X.shape[2]+2*self.padding])
        new_X[:, self.padding:X.shape[1]+self.padding, self.padding:X.shape[2]+self.padding] = X
        u, v = weight.shape
        output_w = (new_X.shape[1] - u) // self.stride + 1
        output_h = (new_X.shape[2] - v) // self.stride + 1
        output = torch.zeros([X.shape[0], output_w, output_h])
        for i in range(0, output.shape[1]):
            for j in range(0, output.shape[2]):
                output[:, i, j] = torch.sum(
                    new_X[:, self.stride*i:self.stride*i+u, self.stride*j:self.stride*j+v]*weight, 
                    axis=[1,2])
        return output

    def forward(self, inputs):
        """
        输入：
            - inputs：输入矩阵，shape=[B, D, M, N]
            - weights：P组二维卷积核，shape=[P, D, U, V]
            - bias：P个偏置，shape=[P, 1]
        """
        feature_maps = []
        # 进行多次多输入通道卷积运算
        p=0
        for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
            multi_outs = []
            # 循环计算每个输入特征图对应的卷积结果
            for i in range(self.in_channels):
                single = self.single_forward(inputs[:,i,:,:], w[i])
                multi_outs.append(single)
                # print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
            # 将所有卷积结果相加
            feature_map = torch.sum(torch.stack(multi_outs), axis=0) + b #Zp
            feature_maps.append(feature_map)
            # print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
            p+=1
        # 将所有Zp进行堆叠
        out = torch.stack(feature_maps, 1) 
        return out
#创建第一层卷积核
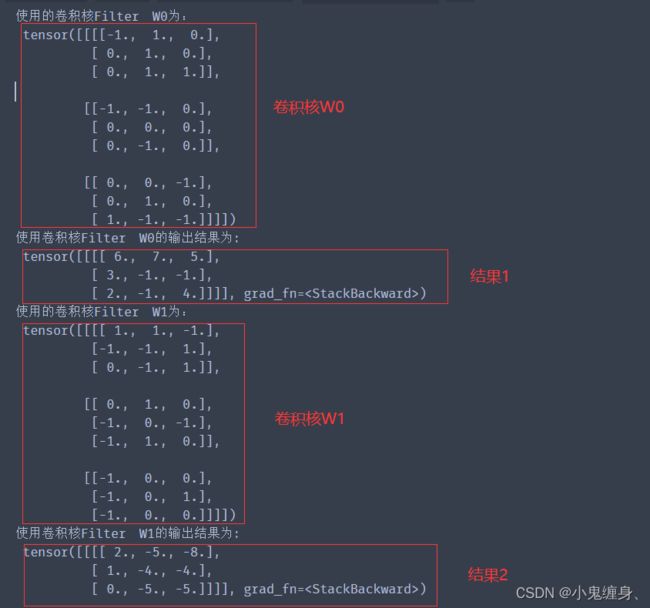
weight_attr1 = torch.tensor([[[-1,1,0],[0,1,0],[0,1,1]],[[-1,-1,0],[0,0,0],[0,-1,0]],[[0,0,-1],[0,1,0],[1,-1,-1]]],dtype=torch.float32)
weight_attr1 = weight_attr1.reshape([1,3,3,3])
bias_attr1 = torch.tensor(torch.ones([3,1]))
print("使用的卷积核Filter　W0为：\n",weight_attr1)
#传入参数进行输出
Input_Volume = torch.tensor([[[0,1,1,0,2],[2,2,2,2,1],[1,0,0,2,0],[0,1,1,0,0],[1,2,0,0,2]]
                ,[[1,0,2,2,0],[0,0,0,2,0],[1,2,1,2,1],[1,0,0,0,0],[1,2,1,1,1]],
               [[2,1,2,0,0],[1,0,0,1,0],[0,2,1,0,1],[0,1,2,2,2],[2,1,0,0,1]]])
Input_Volume = Input_Volume.reshape([1,3,5,5])
conv2d_1 = Conv2D(in_channels=3, out_channels=3, kernel_size=3, stride=2,padding=1,weight_attr=weight_attr1 , bias_attr=bias_attr1)
output1 = conv2d_1(Input_Volume)
print("使用卷积核Filter　W0的输出结果为:\n",output1)

#创建第二层卷积核
weight_attr2 = torch.tensor([[[1,1,-1],[-1,-1,1],[0,-1,1]],[[0,1,0],[-1,0,-1],[-1,1,0]],[[-1,0,0],[-1,0,1],[-1,0,0]]],dtype=torch.float32)
weight_attr2 = weight_attr2.reshape([1,3,3,3])
bias_attr2 = torch.tensor(torch.zeros([3,1]))
print("使用的卷积核Filter　W1为：\n",weight_attr2)
Input_Volume = torch.tensor([[[0,1,1,0,2],[2,2,2,2,1],[1,0,0,2,0],[0,1,1,0,0],[1,2,0,0,2]]
                ,[[1,0,2,2,0],[0,0,0,2,0],[1,2,1,2,1],[1,0,0,0,0],[1,2,1,1,1]],
               [[2,1,2,0,0],[1,0,0,1,0],[0,2,1,0,1],[0,1,2,2,2],[2,1,0,0,1]]])
Input_Volume = Input_Volume.reshape([1,3,5,5])
conv2d_2 = Conv2D(in_channels=3, out_channels=2, kernel_size=3, stride=2,padding=1,weight_attr=weight_attr2 , bias_attr=bias_attr2)
output2 = conv2d_2(Input_Volume)
print("使用卷积核Filter　W1的输出结果为:\n",output2)

输出结果：

---

总结

本节通过对多通道卷积算子的实现和对汇聚层算子的实现，再到自己编写代码实现多通道的卷积操作，之前一直使用的是灰度图，但是灰度图毕竟是单通道的，老师之前讲过多通道，但是当时对多通道的概念不是很清楚，也不太理解多通道的卷积操作，看着最后一个实验，然后传参实现，感觉还是很有成就感的，同时理解了上课老师说的多通道卷积和汇聚，以及步长的作用和填充的效果示意，最后的感觉只有一句话：没有实践的理论是没有效果的。还是收获挺大，对卷积神经网络的了解更深了感觉，同时也有点开始喜欢做实验la，hhhhhhhha。

References:

CS231n Convolutional Neural Networks for Visual Recognition
torch.Tensor
torch.nn.MaxPool2d详解
NNDL 实验5（上）
NNDL 实验5（下）
卷积神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
现代卷积神经网络 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)
附上老师的博客：
NNDL 实验六 卷积神经网络（2）基础算子