梯度下降法实现线性回归
梯度下降法实现线性回归
一、梯度下降法的简单介绍
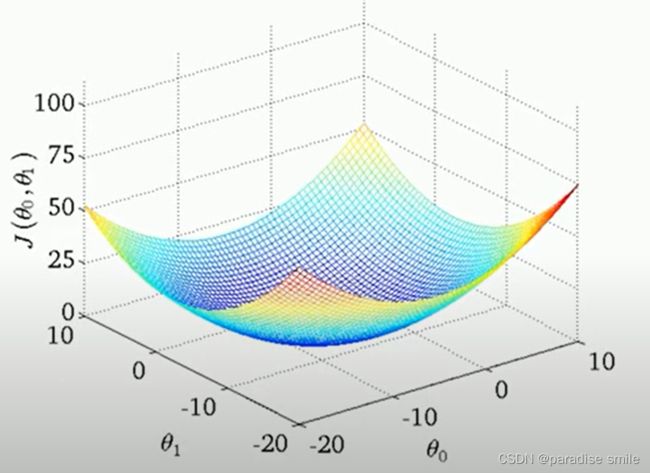
1.梯度下降法寻找全局最小值的过程
不能保证梯度下降法总是能够找到全局最小值,有时还可能找到局部最小值,这也是梯度下降法的缺点。
repeat until convergence{
θ j : = θ j − α ∂ J ( θ 0 , θ 1 ) ∂ θ j ( f o r j = 0 a n d j = 1 ) \theta_{j} := \theta_{j} - \alpha\frac{\partial J(\theta_{0}, \theta_{1})}{\partial{\theta_{j}}} \quad (for\ j =0\ and\ j=1) θj:=θj−α∂θj∂J(θ0,θ1)(for j=0 and j=1)
}
其中α为学习率
学习率不可以太小,也不可以太大,可以多尝试一些值0.1, 0.03, 0.01, 0.0001…
如果学习率过小,寻找全局最小值的时间会过长
如果学习率过大,可能会导致调整的时候过大,找不到全局最小值,陷入局部极小值
二、线性回归的模型和代价函数
h θ = θ 1 x + θ 0 h_{\theta} = \theta_{1}x + \theta_{0} hθ=θ1x+θ0
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_{0},\theta_{1}) = \frac{1}{2m} \sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
∂ J ( θ 0 , θ 1 ) ∂ θ j = { j = 0 : ∂ J ( θ 0 , θ 1 ) ∂ θ 0 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) j = 1 : ∂ J ( θ 0 , θ 1 ) ∂ θ 1 = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) \frac{\partial J(\theta_{0},\theta_{1})}{\partial\theta_{j}} = \begin{cases} j = 0:\quad \frac{\partial J(\theta_{0}, \theta_{1})}{\partial \theta_{0}} = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})\\ j=1 : \quad \frac{\partial J(\theta_{0}, \theta_{1})}{\partial \theta_{1}} = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)} \end{cases} ∂θj∂J(θ0,θ1)={j=0:∂θ0∂J(θ0,θ1)=m1∑i=1m(hθ(x(i))−y(i))j=1:∂θ1∂J(θ0,θ1)=m1∑i=1m(hθ(x(i))−y(i))x(i)
repeat until convergence
{
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \theta_{0} := \theta_{0} - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)}) θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) \theta_{1} := \theta_{1} - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)}) - y^{(i)})x^{(i)} θ1:=θ1−αm1i=1∑m(hθ(x(i))−y(i))x(i)
}
线性回归的代价函数是凸函数
三、代码实现
import numpy as np
import matplotlib.pyplot as plt
# 导入数据
x_data = np.array([0, 1, 2, 3, 4])
y_data = np.array([1.5, 2.5, 3.8, 5.0, 7.5])
y_data = np.log(y_data)
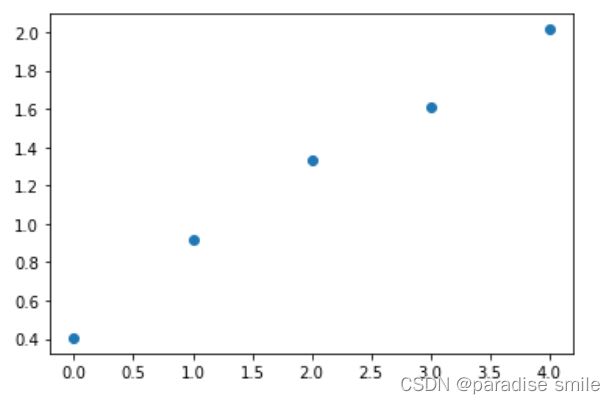
plt.scatter(x_data, y_data)
plt.show()
# 步长
lr = 0.01
#截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 5000
#最小二乘法
def computer_error(b, k, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (k*x_data[i] + b)) ** 2 #代价函数
return totalError / float(len(x_data)) / 2.0
def tdxj(x_data, y_data, b, k, lr, epoches):
# 计算
m = float(len(x_data))
# 循环i次
for i in range(epochs):
b_grad = 0
k_grad = 0
# 计算梯度的总和求平均
for j in range(0, len(x_data)):
b_grad += -(1/m) * (y_data[j] - ((k * x_data[j]) + b))
k_grad += -(1/m) * x_data[j] * (y_data[j] - ((k * x_data[j]) + b))
# 更新b和k
b = b - (lr * b_grad)
k = k - (lr * k_grad)
return b, k
b, k = tdxj(x_data, y_data, b, k, lr, epochs)
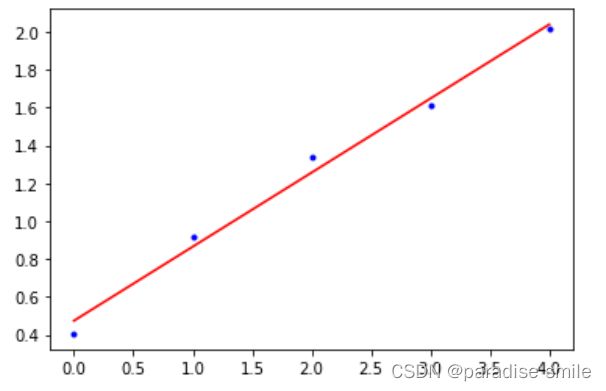
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data+b, 'r')
plt.show()
b = np.exp(b)
b
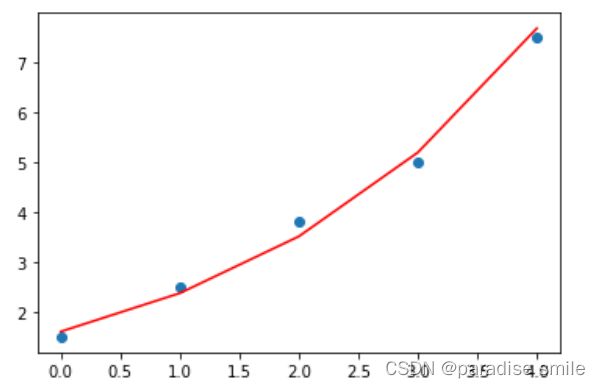
plt.plot(x_data,b*np.exp(k*x_data),'r')
y_data = np.array([1.5, 2.5, 3.8, 5.0, 7.5])
plt.scatter(x_data, y_data)