支持向量机SVM

支持向量机SVM

1.SVM历史

1. 最早是由Vladimir N. Vapnik 和Alexey Ya.Chervonenkis在1963年提出
2. 目前的版本(soft margin)是由Corinna Cortes和Vapnik在1993年提出，并在1995年发表
3. 深度学习(2012)出现之前，SVM被认为是机器学习近十年来最成功的，表现最好的算法

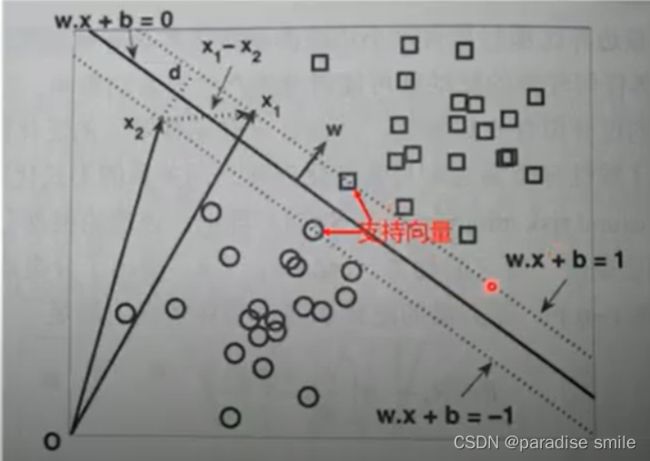
SVM寻找区分两类的超平面(hyper plane)，使边际(margin)最大

向量内积

$$\left\{\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right\}\left\{\begin{array}{c}{y}_1\\ y_2\\ ...\\ y_n\end{array}\right\}$$

向量内积：
$$x\cdot y=x_1{y}_1+x_2{y}_2+...+x_n{y}_n$$
向量内积：
$$x\cdot y=\Vert \begin{array}{c}x\end{array}\Vert \Vert \begin{array}{c}y\end{array}\Vert cos(\theta )$$
范数：
$$\Vert \begin{array}{c}x\end{array}\Vert =\sqrt{x\cdot x}=\sqrt{x_1^2+x_2^2+x_3^2+...x_n^2}$$
当||x|| ≠ 0, ||y||≠0时，可以求余弦相似度：
$$cos(\theta )=\frac{x\cdot y}{\Vert \begin{array}{c}x\end{array}\Vert \Vert \begin{array}{c}y\end{array}\Vert }$$

一些推导

$$\begin{gathered} w\cdot x+b=1 \\ w\cdot x+b=-1 \\ w\cdot (x_1-x_2)=2 \\ \Vert \begin{array}{c}w\end{array}\Vert \Vert \begin{array}{c}(x_1-x_2)\end{array}\Vert cos(\theta )=2 \\ \Vert \begin{array}{c}w\end{array}\Vert \ast d=2 \\ d=\frac{2}{\Vert \begin{array}{c}w\end{array}\Vert } \end{gathered}$$

转为凸优化

$$\begin{gathered} w\cdot x+b\ge 1,则分类y=1 \\ w\cdot x+b\le 1,则分类y=-1 \\ 则y(w\cdot x+b)\ge 1 \\ 求d=\frac{2}{\Vert \begin{array}{c}w\end{array}\Vert }最大值，也就是求min\frac{{\Vert \begin{array}{c}w\end{array}\Vert }^2}{2} \end{gathered}$$

凸优化问题

1. 无约束优化问题： min f(x)

   ----费马定理

2. 带等式约束的优化问题： min f(x)

   —拉格朗日乘子法：s.t. h_i(x) =0, i=0, 1, 2…n
   $$L(x,\lambda )=f(x)+\sum _{i=1}^n{\lambda }_i{h}_i(x)$$

4. 带不等式约束的优化问题： min f(x)

   —KTT条件 s.t. h_i(x) = 0, i=1, 2,…,n

   ​ g_i(x) ≤ 0， i=1,2,…,k
   $$L(x,\lambda ,v)=f(x)+\sum _{i=1}^k{\lambda }_i{g}_i(x)+\sum _{i=1}^n{v}_i{h}_i(x)$$

广义拉格朗日乘子法

$$L(w,b,a)=\frac{1}{2}{\Vert \begin{array}{c}w\end{array}\Vert }^2-\sum _{i=1}^n{\alpha }_i(y_i(w^T{x}_i+b)-1)$$

$$\frac{\partial L}{\partial w}=0\to w=\sum _{i=1}^n{\alpha }_i{y}_i{x}_i$$

$$\frac{\partial L}{\partial b}=0\to \sum _{i=1}^n{\alpha }_i{y}_i=0$$

进一步简化为对偶问题

上述问题可以改写为：
$$\underset{w,b}{\min }\underset{a_i\ge 0}{\max }L(w,b,\alpha )=p^{\ast }$$
可以等价为下列对偶问题：
$$\underset{a_i\ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha )=d^{\ast }$$
把w和b消除掉
$$L(w,b,\alpha )=\sum _{i=1}^n{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$

$$\underset{a_i\ge 0}{\max }\underset{w,b}{\min }L(w,b,\alpha )=\underset{\alpha }{\max }[\sum _{i=1}^k{\alpha }_i-\frac{1}{2}\sum _{i,j=1}^k{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{)}^T{x}_j]$$

约束条件：
$$s.t.\sum _{i=1}^k{a}_i{y}_i=0,a_i\ge 0,i=1,2,....n$$
进一步转化为
$$\underset{\alpha }{\min }[-\sum _{i=1}^k{\alpha }_i+\frac{1}{2}\sum _{i,j=1}^k{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{)}^T{x}_j]=\underset{\alpha }{\min }[-\sum _{i=1}^k{\alpha }_i+\frac{1}{2}\sum _{i,j=1}^k{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)]$$
由此可以求出最优解α*，求出该值后将其带入可以得到：
$$w^{\ast }=\sum _{i=1}^n{a}_i^{\ast }{y}_i{x}_i$$

$$b^{\ast }=y_i-(w^{\ast }{)}^T{x}_i$$

SMO算法

Microsoft Research的John C.Platt在1998年提出针对线性SVM和数据稀疏时性能更优

基本思路：先根据约束条件随机给α赋值。然后每次选取两个α，调节这两个alpha使得目标函数最小。然后再选取两个α，调节α使得目标函数最小。以此类推

SVM简单实例

可知目标函数为
$$\underset{\alpha }{\min }f(\alpha ),s.t.{\alpha }_1+{\alpha }_2-{\alpha }_3=0,{\alpha }_i\ge 0,i=1,2,3$$
其中
$$\begin{gathered} f(\alpha )=\frac{1}{2}\sum _{i,j=1}^3{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^3{\alpha }_i \\ =\frac{1}{2}(18{\alpha }_1^2+25{\alpha }_2^2+2{\alpha }_3^2+42{\alpha }_1{\alpha }_2-12{\alpha }_1{\alpha }_3-14{\alpha }_2{\alpha }_3)-{\alpha }_1-{\alpha }_2-{\alpha }_3 \end{gathered}$$
然后，将α3 = α1 + α2带入到目标函数，得到一个关于α1和α2的函数
$$s({\alpha }_1,{\alpha }_2)=4{\alpha }_1^2+\frac{13}{2}{\alpha }_2^2+10{\alpha }_1{\alpha }_2-2{\alpha }_1-2{\alpha }_2$$
对α1和α2求偏导数并令其为0，易知s(α1，α2)在点（1.5， -1）处取极值。而该点不满足αi≥0的约束条件，于是可以推断最小值在边界上达到。经计算当α1 = 0时，s(α1=0,α2=2/13)=-0.1538;当α2=0时，s(α1=1/4, α2=0)=-0.25.于是s(α1,α2)在α1=1/4，α2=0时取得最小值，此时亦可以算出α3 = α1 + α2 = 1/4.因为α1和α3不等于0，所以对应的点x1和x3就应该是支持向量。
$$w^{\ast }=\sum _{i=1}^3{a}_i^{\ast }{y}_i{x}_i=\frac{1}{4}\cdot (3,3)+\frac{1}{4}(1,1)=(\frac{1}{2},\frac{1}{2})$$
即w1 = 0.5, w2=0.5,进而有
$$b^{\ast }=1-(w_1,w_2)\cdot (3,3)=-2$$
因此最大间隔分类超平面为
$$\frac{1}{2}{x}_1+\frac{1}{2}{x}_2-2=0$$
分类决策函数为
$$f(x)=sign(\frac{1}{2}{x}_1+\frac{1}{2}{x}_2-2)$$

SVM优点

• 训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的，所以SVM不太容易产生overfitting
• SVM训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型
• 一个SVM如果训练得出的支持向量个数比较小，SVM训练出来的模型比较容易被泛化