堆排序

一开始感觉这个最难所以放到最后来写。

堆排序

In computer science, heapsort is a comparison-based sorting algorithm.Heapsort can be thought of as an improved selection sort: like
selection sort, heapsort divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by
extracting the largest element from it and inserting it into thesorted region. Unlike selection sort, heapsort does not waste time
with a linear-time scan of the unsorted region; rather, heap sort maintains the unsorted region in a heap data structure to more quickly
find the largest element in each step.[1]

Although somewhat slower in practice on most machines than a well-implemented quicksort, it has the advantage of a more favorable
worst-case O(n log n) runtime. Heapsort is an in-place algorithm, but it is not a stable sort.

Heapsort was invented by J. W. J. Williams in 1964.[2] This was also the birth of the heap, presented already by Williams as a useful data
structure in its own right.[3] In the same year, R. W. Floyd published an improved version that could sort an array in-place, continuing his
earlier research into the treesort algorithm.[3]
from：https://en.wikipedia.org/wiki/Heapsort

（插一句嘴即使是维基百科，英文版的内容详实程度和质量也要强过中文版很多，虽然英文版阅读起来会有些障碍速度也会慢，但请相信它绝对能提升你理解的效率，最后推荐一下谷歌浏览器里有个叫划词翻译的插件很好用）

译：
在计算机科学中，heapsort是一种基于比较的排序算法。可以将Heapsort视为一种改进的选择排序：类似于选择排序，heapsort将其输入分为已排序和未排序的区域，并通过从中提取最大元素并将其插入已排序区域来迭代地缩小未排序区域。与选择排序不同，堆排序不会对未排序区域进行线性时间扫描，因此不会浪费时间。相反，堆排序可在堆数据结构中维护未排序的区域，以便在每个步骤中更快地找到最大的元素。
[1]尽管在大多数机器上实践中的速度比快速实施的快速排序稍慢，但它具有更有利的最坏情况O（n log n）运行时的优点。Heapsort是一种就地算法，但不是稳定的排序。Heapsort由J.W. J. Williams于1964年发明。[2]这也是堆的诞生，威廉姆斯已经将堆本身作为一种有用的数据结构提出了。[3]同年，R。W. Floyd发布了改进的版本，可以对数组进行原位排序，从而继续了他对treesort算法的早期研究。

---

堆排序基本思想及步骤

---

该段图文转自：https://www.cnblogs.com/rosesmall/p/9554545.html
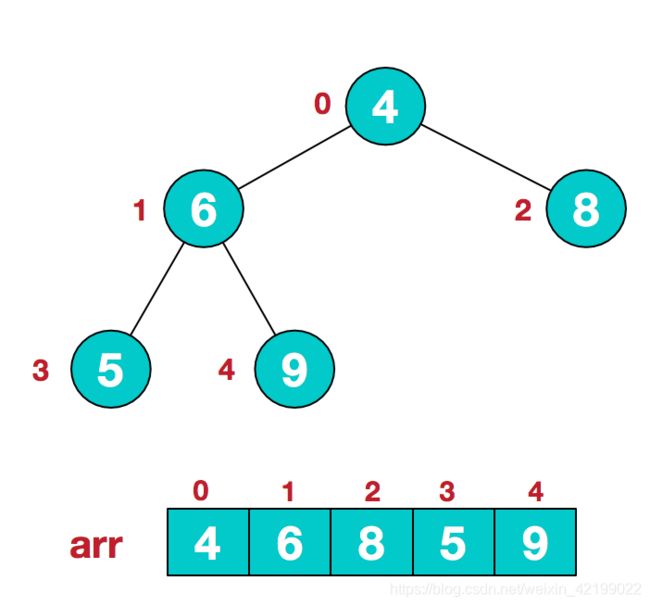
　　堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

a.假设给定无序序列结构如下

2.此时我们从后往前，从下往上的第一个非叶子节点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。
注：（关于从下往上第一个非叶子节点(n/2-1)的问题在我代码的注释里我会详细说一·下）

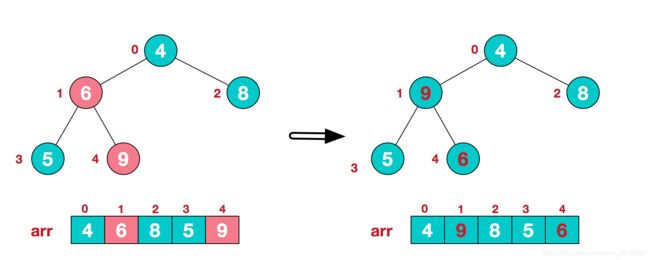
4.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

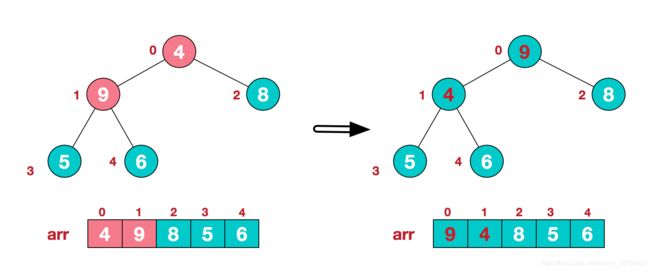
这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

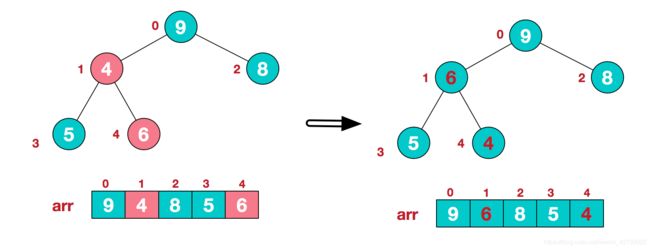
此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

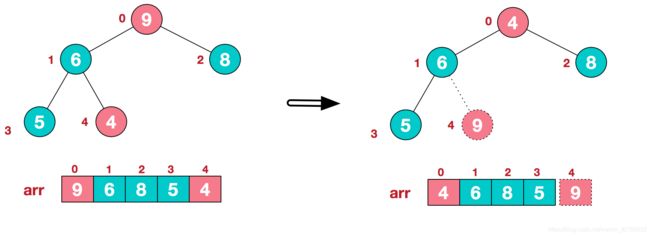
a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构，使其继续满足堆定义

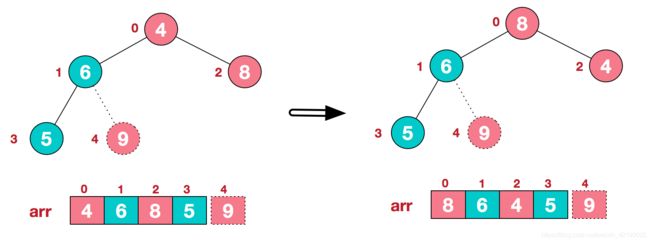
c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

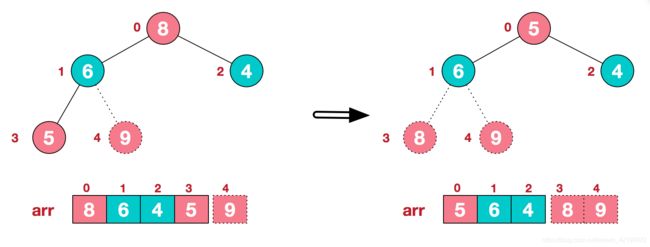
后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

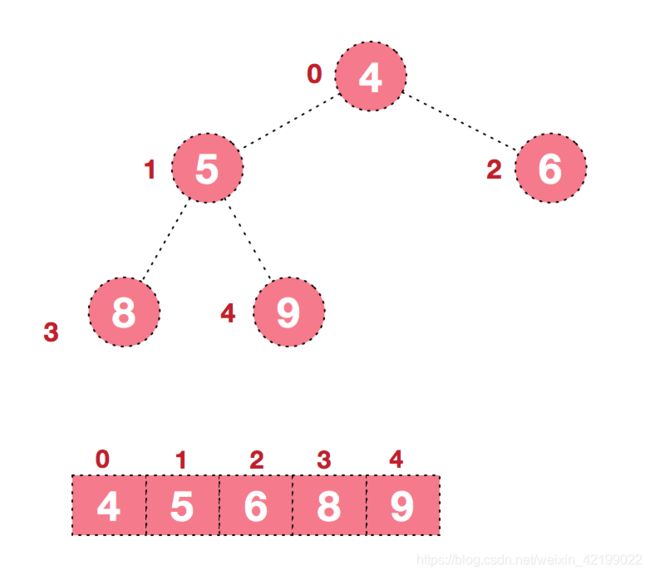
再简单总结下堆排序的基本思路：

a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

代码
main.cpp

#include"head.h"


int main()
{
	
	int  len;
	int  a[MaxSize];
	cout << "输入随机数组元素个数" << endl;
	cin >> len;
	cout << endl;
	cout << "生成一个元素个数为" << len << "的随机数组" << endl;
	Array_generate(a, len);
    cout << endl;

   
	cout <<" 堆排序结果如下：" << endl;
	Heap_sort(a,len);
    for (int i = 0; i < len; ++i)
        cout << setw(3)<<a[i];   
    return 0;

head.h

#include
#include
#include 

using namespace std;

#define MaxSize 30
void  Max_heap(int a[],int len,int index);
void  Heap_sort(int a[],int len);
void Array_generate(int a[], int len);

operation.cpp

#include"head.h"
void Array_generate(int a[], int len)//生成一个随机数组
{
	srand(time(NULL));
	for (int i = 0;i < len;i++)
	{
		a[i] = rand() % 100;
	}
	for (int j = 0;j < len;j++)
	{
		cout << setw(3) << a[j];
	}
	cout << endl;
}
void Max_heap(int a[],int len,int index) //index是指最后一个非叶子节点下标
{
	if (index > len)
	{
		return;
	}
	int left = 2 * index + 1; // 最后一个非叶子的左子节点
	int right = 2 * index + 2;// 最后一个非叶子节点的右子节点
	int max = index;

	if (left<len && a[left] > a[max])     max = left;
	if (right<len && a[right] > a[max])     max = right;

	if (max != index)
	{
		swap(a[max], a[index]);
		Max_heap(a, len, max);
	}

}
void Heap_sort(int a[], int len)
{
	for (int i = len / 2 - 1; i >= 0; i--)	// 构建大顶堆
	{
		Max_heap(a, len, i);
	}
     /*关于i=len / 2 - 1的问题*/
	/*
	根据完全二叉树的性质：如果节点序号为i，在它的左孩子序号为2*i+1， 
	右孩子序号为2*i+2。
	
	假设有这两种情况：
	①堆的最后一个非叶子节点若只有左孩子
    ②堆的最后一个非叶子节点有左右两个孩子

	当数组长度为n
    对于①左孩子的序号为n-1，则n-1=2*i+1，推出i=n/2-1；
    对于②左孩子的序号为n-2，在n-2=2*i+1，推出i=(n-1)/2-1；
      右孩子的序号为n-1，则n-1=2*i+2，推出i=(n-1)/2-1；

    很显然，当完全二叉树最后一个节点是其父节点的左孩子时，树的节点数为偶数；
	当完全二叉树最后一个节点是其父节点的右孩子时，树的节点数为奇数。 
    根据向下取整原则，则若n为奇数时(n-1)/2-1=n/2-1。

    也可以这样理解就是当节点个数为奇数个时与节点个数取
    这个奇数向下最近的偶数时它们的最后一个非叶子节点是一样的。
	最简单的理解就是在第一种情况上加一个节点就是第二种情况
	*/
	for (int i = len - 1; i >= 1; i--)
	{
		swap(a[0], a[i]);           // 将当前最大的放置到数组末尾
		Max_heap(a, i, 0);              
	}

}

Bottom-up heapsort

Bottom-up heapsort is a variant which reduces the number of comparisons required by a significant factor. While ordinary heapsort requires 2n log2n + O(n) comparisons worst-case and on average,[8] the bottom-up variant requires n log2n + O(1) comparisonson average,[8] and 1.5n log2n + O(n) in the worst case.[9]If comparisons are cheap (e.g.integer keys) then the difference is unimportant,[10] as top-down heapsort compares values that havealready been loaded from memory. If, however, comparisons require afunction call or other complex logic, then bottom-up heapsort is advantageous.

This is accomplished by improving the siftDown procedure. The change
improves the linear-time heap-building phase somewhat,[11] but is more
significant in the second phase. Like ordinary heapsort, each iteration of the second phase extracts the top of the heap, a[0], and fills the gap it leaves with a[end], then sifts this latter element down the heap. But this element comes from the lowest level of the heap, meaning it is one of the smallest elements in the heap, so the sift-down will likely take many steps to move it back down. In ordinary heapsort, each step of the sift-down requires two comparisons, to find the minimum of three elements: the new node and its two children.

Bottom-up heapsort instead finds the path of largest children to the leaf level of the tree (as if it were inserting −∞) using only one comparison per level. Put another way, it finds a leaf which has the property that it and all of its ancestors are greater than or equal to their siblings. (In the absence of equal keys, this leaf is unique.) Then, from this leaf, it searches upward (using one comparison per level) for the correct position in that path to insert a[end]. This is the same location as ordinary heapsort finds, and requires the same number of exchanges to perform the insert, but fewer comparisons are required to find that location.[9]
Because it goes all the way to the bottom and then comes back up, it is called heapsort with bounce by some authors.[12]

译：
自下而上的堆排序
自下而上的堆排序是一个变体，可将所需的比较次数减少很多。
普通堆排序最坏情况下平均需要2nlog2n + O（n）比较，[8]自下而上的变体平均需要[8] nloglog2n + O（1）比较，以及1.5n log2n + O（n）比较
）在最坏的情况下。[9]
如果比较便宜（例如整数键），则差异不重要[10]，因为自顶向下的堆排序将比较已从内存中加载的值。
但是，如果比较需要函数调用或其他复杂的逻辑，则自下而上的堆排序将是有利的。
这可以通过改进siftDown过程来完成。
该更改在某种程度上改善了线性时间堆构建阶段，[11]但在第二阶段更有意义。
像普通的堆排序一样，第二阶段的每次迭代都提取堆的顶部a [0]，并用a [end]填充它留下的间隙，然后将后一个元素向下过滤到堆中。
但是此元素来自堆的最低层，这意味着它是堆中最小的元素之一，因此筛选可能会花费很多步骤才能将其移回堆。
在普通的堆排序中，筛选的每个步骤都需要进行两次比较，以查找最少三个元素：新节点及其两个子节点。
自下而上的堆排序仅使用每个级别的一个比较来查找最大子级到树的叶子级别的路径（就像在插入-∞一样）。
换句话说，它找到一个叶子，该叶子具有其及其所有祖先大于或等于其兄弟姐妹的属性。
（在没有相等键的情况下，此叶子是唯一的。）然后，从该叶子向上搜索（使用每个级别一个比较）以在该路径中插入a [end]的正确位置。
这是与普通堆排序所找到的位置相同的位置，并且需要相同数量的交换才能执行插入操作，但是需要较少的比较才能找到该位置。[9]
因为它一直到达底部然后又重新出现，所以被某些作者称为带有反弹的堆排序。[12]

function leafSearch(a, i, end) is
    j ← i
    while iRightChild(j) ≤ end do
        (Determine which of j's two children is the greater)
        if a[iRightChild(j)] > a[iLeftChild(j)] then
            j ← iRightChild(j)
        else
            j ← iLeftChild(j)
    (At the last level, there might be only one child)
    if iLeftChild(j) ≤ end then
        j ← iLeftChild(j)
    return j

The return value of the leafSearch is used in the modified siftDown
routine:[9]
leafSearch的返回值在修改后的siftDown例程中使用

procedure siftDown(a, i, end) is
    j ← leafSearch(a, i, end)
    while a[i] > a[j] do
        j ← iParent(j)
    x ← a[j]
    a[j] ← a[i]
    while j > i do
        swap x, a[iParent(j)]
        j ← iParent(j)

（先写到这吧有人看我再更吧）