numpy的基本操作

有关numpy的基本操作

numpy 有关dim shape dtype 属性

属性	描述
dim	维数，即[]里面 有几个[]
shape	几行几列的
dtype	数据类型
sum	相加

代码示例如下： ndim shape dtype

import  numpy as np
array_1x6=np.array([[1.0,2.0,3.0],
                    [4.0,5.0,6.0]])
print(array_1x6)
print(array_1x6.ndim)
print(array_1x6.shape)
print(array_1x6.dtype)

运行结果：

ndarry中的axes的定义：
二维数组：
axes0,axes1
三维数组：
axes0,axes1,axes2

有关sum函数

print(array_1x6.sum(axis=0))  # 代表数轴相加
print(array_1x6.sum(axis=1))  # 代表 横轴相加

运行结果：

示例： 二行三列

	5	7	9
6	1	2	3
15	4	5	6

矢量化运算

numpy的数组通常在不用编写循环的情况下进行批量运算。十分方便
他可以用简洁的表达代替for in 循环 高效处理打滚哦数组的优势。

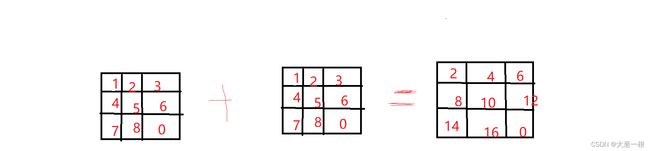
代码示例：

import  numpy as np
array_43_a=np.array([[1,1,1],
                    [2,2,2],
                    [3,3,3],
                    [4,4,4]])
array_43_b=np.array([[5,5,5],
                    [6,6,6],
                    [3,3,3],
                    [4,4,4]])

print(array_43_a+array_43_b)

结果如下：

数组的广播：
较小的数组广播到大数组相同的形状尺度上，使他们对等的进行数学运算，其中最简单的广播场景是一个数组和一个标量运算。同时省时间

数组的广播存在兼容问题
（x，y）+(z,y) 兼容
常用的元素级处理函数

创建数组函数：

功能	函数	描述
创建不同元素值的多维数组	numpy.array()	根据输入数据创建多为数组
创建不同元素值的多维数组	numpy.ones()	根据元素全为1多维数组
创建不同元素值的多维数组	numpy.zeros()	根据元素全为0多维数组
创建不同元素值的多维数组	numpy.full()	根据输入数据创建多为数组
创建指定元素值的二维数组	numpy.eye()	创建对角矩阵形式的二维数组
创建指定元素值的一维数组	numpy.linspace() numpy.arange()	创建等差数列的一维数组
创建随机元素值的二维数组	numpy.random.randint()	创建指定上下限范围的随机数组
创建随机元素值的二维数组	numpy.random.randn()	创建符合正态分布的随机数组
创建随机元素值的二维数组	numpy.random.binomial()	创建符合二项分布的随机数组
创建随机元素值的二维数组	numpy.random.rand()	创建[0,1)符合均匀分布的随机数组

元素级数组函数

一元函数

函数	描述
numpy.abs()	计算数组元素的绝对值
numpy.exp()	计算数组元素的指数
numpy.sqrt()	计算数组元素的开方 （根号）
numpy.sign()	计算数组元素的正负号
numpy.isnan()	计算数组元素是否为NaN

二元函数

函数	描述
numpy.add()	计算数组之间相加+
numpy.multiply()	计算数组之间相乘
numpy.subtract()	计算数组之间相减
numpy.divide()	计算数组之间相除
三元表达式 numpy.where()	if x condition else y (如果满足返回x 否则返回y)

红色部分代码示例：

# coding=gbk
import numpy as np
# full(shape, fill_value, dtype=None, order='C', *, like=None):
# 2行4列全为10
array_full=np.full(shape=(2,4),fill_value=10)
print(array_full)
# 主对角线元素为1
array_eye= np.eye(4,M=4)
print(array_eye)
# def linspace (start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0):
# 等差数列 从0开始到10结束 一共有10个数
array_linspace= np.linspace(start=0,stop=10,num=10,endpoint=False)
print(array_linspace)
# sign的用法
array_33=np.array([[-1,1,-1],
                  [2,-2,2],
                  [3,-3,-3]])
array_sign=np.sign(array_33)
print(array_sign)

# 返回true或者false
array_22=np.array([[np.nan,1],
                   [2,np.nan]])
array_nsign=np.isnan(array_22)
print(array_nsign)


array_43=np.array([
    [1,1,1],
    [-2,8,2],
    [3,9,3],
    [4,4,-4]

])
#def where(condition, x=None, y=None):  满足返回x 否则返回y
array_where=np.where(array_43>5,5,0)
print(array_where)

随机变量分布数组的生成

相关概念：随机事件、概率、随机变量、随机变量根据可能取得的值
相关的函数
常见的离散随机变量分布：均匀分布、指数分布，正态分布
伯努利试验：是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。

函数	描述
伯努利试验接口 numpy.random.binomial(n,p,size=None)	n-实验次数 p-某事件发生的概率 size-表示n次伯努利试验的次数
正态分布 numpy.random.normal(n,p,size=None)	还有一些其他的参数 loc-期望u scale-标准差

例如 抛硬币 抛n=5次硬币每次正面朝上的概率为p=0.5 试验一共进行了size=10次
代码示例：

# coding=gbk
import numpy as np
# 返回 一维数组
# 做5次试验 发生的概率为0.5  规模为10 例如  抛5次硬币 每次概率为0.5 这个试验进行了了10次
array_binomial=np.random.binomial(5,0.5,size=10)
print(array_binomial)
# 输出结果 [3 2 3 1 3 3 2 2 2 5]   抛5次硬币 每次概率为0.5 进行了10次

# 返回二维数组
array_binomial_34=np.random.binomial(5,0.5,size=(3,4))
print(array_binomial_34)
# 期望172.7 标准差4.01  次数1000
array_normal=np.random.normal(loc=172.7,scale=4.01,size=1000)
print(array_normal)