pytorch学习笔记（四）——MNIST数据集实战

目录

神经网络运作流程

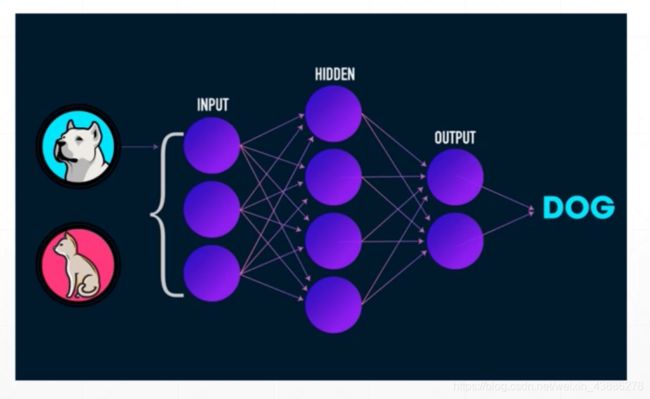
上图所示是一个简单的二层神经网络结构，猫和狗的图片作为输入，依次是输入层，隐层，输出层。每张图片作为输入经过模型得到输出判别是猫还是狗，将输入与真实值之间求误差，再对误差求梯度优化参数w和b，使最后得到的误差尽可能小。

回顾

上一个博客中我们讲到，我们将输入X经过一个线性模型得再通过ReLU激活函数得到H1，在经过一次ReLU得到H2，最后一层通常并不使用ReLU激活函数，常见的有sigmoid，softmax的函数，这里我们直接通过一个线性模型得到H3，即为最终的预测输出。

识别的四个步骤

1.首先通过pytorch自带函数完成minist数据集的下载，解析，读取图片
2.建立如上图所示的三层非线性模型
3.输入训练集完成参数的优化
4.输入测试集对训练好的模型进行评估

实现代码

辅助代码utils.py

import  torch
from    matplotlib import pyplot as plt


def plot_curve(data):#绘制曲线
    fig = plt.figure()#创建一个图片
    plt.plot(range(len(data)), data, color='blue')
    #图片横坐标为0-数据长度 纵坐标为数据 颜色蓝色
    plt.legend(['value'], loc='upper right')
    plt.xlabel('step')
    plt.ylabel('value')
    #图片横纵坐标的label
    plt.show()
    #显示图片


def plot_image(img, label, name):#显示图片

    fig = plt.figure()#创建一个图片对象
    for i in range(6):
        plt.subplot(2, 3, i + 1)#子图
        plt.tight_layout()#自动调整子图参数 未必会工作
        plt.imshow(img[i][0]*0.3081+0.1307, cmap='gray', interpolation='none')
        #之前做了标准化 这里把他恢复
        plt.title("{}: {}".format(name, label[i].item()))
        #label[i].item()把tensor类型转换为python格式类型
        plt.xticks([])
        plt.yticks([])
    plt.show()


def one_hot(label, depth=10):#实现一位热编码
    out = torch.zeros(label.size(0), depth)
    idx = torch.LongTensor(label).view(-1, 1)
    out.scatter_(dim=1, index=idx, value=1)
    return out

核心代码mnist.py

import  torch
from    torch import nn
from    torch.nn import functional as F
from    torch import optim

import  torchvision
from    matplotlib import pyplot as plt

from    utils import plot_image, plot_curve, one_hot



batch_size = 512

# step1. load dataset
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), x.max())
plot_image(x, y, 'image sample')



class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()

        # xw+b
        self.fc1 = nn.Linear(28*28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        # x: [b, 1, 28, 28]
        # h1 = relu(xw1+b1)
        x = F.relu(self.fc1(x))
        # h2 = relu(h1w2+b2)
        x = F.relu(self.fc2(x))
        # h3 = h2w3+b3
        x = self.fc3(x)

        return x



net = Net()
# [w1, b1, w2, b2, w3, b3]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)


train_loss = []

for epoch in range(3):

    for batch_idx, (x, y) in enumerate(train_loader):

        # x: [b, 1, 28, 28], y: [512]
        # [b, 1, 28, 28] => [b, 784]
        x = x.view(x.size(0), 28*28)
        # => [b, 10]
        out = net(x)
        # [b, 10]
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = F.mse_loss(out, y_onehot)

        optimizer.zero_grad()
        loss.backward()
        # w' = w - lr*grad
        optimizer.step()

        train_loss.append(loss.item())

        if batch_idx % 10==0:
            print(epoch, batch_idx, loss.item())

plot_curve(train_loss)
# we get optimal [w1, b1, w2, b2, w3, b3]


total_correct = 0
for x,y in test_loader:
    x  = x.view(x.size(0), 28*28)
    out = net(x)
    # out: [b, 10] => pred: [b]
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct

total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test acc:', acc)

x, y = next(iter(test_loader))
out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')