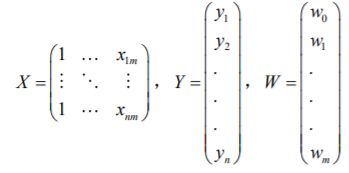
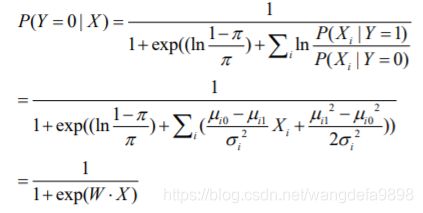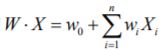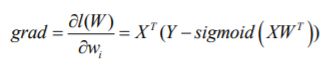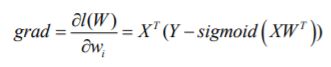- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- 数字里的世界17期:2021年全球10大顶级数据中心,中国移动榜首
张三叨
你知道吗?2016年,全球的数据中心共计用电4160亿千瓦时,比整个英国的发电量还多40%!前言每天,我们都会创造超过250万TB的数据。并且随着物联网(IOT)的不断普及,这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代,但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术,比如人工智能和机器学习,已经将我们推向
- nosql数据库技术与应用知识点
皆过客,揽星河
NoSQLnosql数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
- Python开发常用的三方模块如下:
换个网名有点难
python开发语言
Python是一门功能强大的编程语言,拥有丰富的第三方库,这些库为开发者提供了极大的便利。以下是100个常用的Python库,涵盖了多个领域:1、NumPy,用于科学计算的基础库。2、Pandas,提供数据结构和数据分析工具。3、Matplotlib,一个绘图库。4、Scikit-learn,机器学习库。5、SciPy,用于数学、科学和工程的库。6、TensorFlow,由Google开发的开源机
- Python实现简单的机器学习算法
master_chenchengg
pythonpython办公效率python开发IT
Python实现简单的机器学习算法开篇:初探机器学习的奇妙之旅搭建环境:一切从安装开始必备工具箱第一步:安装Anaconda和JupyterNotebook小贴士:如何配置Python环境变量算法初体验:从零开始的Python机器学习线性回归:让数据说话数据准备:从哪里找数据编码实战:Python实现线性回归模型评估:如何判断模型好坏逻辑回归:从分类开始理论入门:什么是逻辑回归代码实现:使用skl
- 遥感影像的切片处理
sand&wich
计算机视觉python图像处理
在遥感影像分析中,经常需要将大尺寸的影像切分成小片段,以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务,如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程,同时确保每个影像片段保留正确的地理信息。准备环境首先,确保安装了必要的Python库,包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
- ai绘画工具midjourney怎么下载?附作品管理教程
设计师早上好
Midjourney是一款功能强大的AI绘画工具,它使用机器学习技术和深度神经网络等算法,可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么,ai绘画工具midjourney怎么下载?本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单,只需打开Midjourney官网(点击“GetMidjour
- [实践应用] 深度学习之模型性能评估指标
YuanDaima2048
深度学习工具使用深度学习人工智能损失函数性能评估pytorchpython机器学习
文章总览:YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域,评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标:准确率(
- 机器学习-聚类算法
不良人龍木木
机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记,感谢点赞关注!1.AHC2.K-means3.SC传统谱聚类:个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持!
- 未来软件市场是怎么样的?做开发的生存空间如何?
cesske
软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的?做开发的生存空间如何?一、未来软件市场的发展趋势技术趋势:人工智能与机器学习:随着技术的不断成熟,人工智能将在更多领域得到应用,如智能客服、自动驾驶、智能制造等,这将极大地推动软件市场的增长。云计算与大数据:云计算服务将继续普及,大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率,并
- python中zeros用法_Python中的numpy.zeros()用法
江平舟
python中zeros用法
numpy.zeros()函数是最重要的函数之一,广泛用于机器学习程序中。此函数用于生成包含零的数组。numpy.zeros()函数提供给定形状和类型的新数组,并用零填充。句法numpy.zeros(shape,dtype=float,order='C'参数形状:整数或整数元组此参数用于定义数组的尺寸。此参数用于我们要在其中创建数组的形状,例如(3,2)或2。dtype:数据类型(可选)此参数用于
- 【NumPy】深入解析numpy.zeros()函数
二七830
numpy
欢迎莅临我的个人主页这里是我深耕Python编程、机器学习和自然语言处理(NLP)领域,并乐于分享知识与经验的小天地!博主简介:我是二七830,一名对技术充满热情的探索者。多年的Python编程和机器学习实践,使我深入理解了这些技术的核心原理,并能够在实际项目中灵活应用。尤其是在NLP领域,我积累了丰富的经验,能够处理各种复杂的自然语言任务。技术专长:我熟练掌握Python编程语言,并深入研究了机
- 【中国国际航空-注册_登录安全分析报告】
风控牛
验证码接口安全评测系列安全行为验证极验网易易盾智能手机
前言由于网站注册入口容易被黑客攻击,存在如下安全问题:1.暴力破解密码,造成用户信息泄露2.短信盗刷的安全问题,影响业务及导致用户投诉3.带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞所以大部分网站及App都采取图形验证码或滑动验证码等交互解决方案,但在机器学习能力提高的当下,连百度这样的大厂都遭受攻击导致点名批评,图形验证及交互验证方式的安全性到底如何?请看具体分析一、中国国际航空PC
- 机器学习 流形数据降维:UMAP 降维算法
小嗷犬
Python机器学习#数据分析及可视化机器学习算法人工智能
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。个人主页:小嗷犬的个人主页个人网站:小嗷犬的技术小站个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP(UniformManifoldApproximatio
- 七.正则化
愿风去了
吴恩达机器学习之正则化(Regularization)http://www.cnblogs.com/jianxinzhou/p/4083921.html从数学公式上理解L1和L2https://blog.csdn.net/b876144622/article/details/81276818虽然在线性回归中加入基函数会使模型更加灵活,但是很容易引起数据的过拟合。例如将数据投影到30维的基函数上,模
- 机器学习-------数据标准化
罔闻_spider
数据分析算法机器学习人工智能
什么是归一化,它与标准化的区别是什么?一作用在做训练时,需要先将特征值与标签标准化,可以防止梯度防炸和过拟合;将标签标准化后,网络预测出的数据是符合标准正态分布的—StandarScaler(),与真实值有很大差别。因为StandarScaler()对数据的处理是(真实值-平均值)/标准差。同时在做预测时需要将输出数据逆标准化提升模型精度:标准化/归一化使不同维度的特征在数值上更具比较性,提高分类
- 分享一个基于python的电子书数据采集与可视化分析 hadoop电子书数据分析与推荐系统 spark大数据毕设项目(源码、调试、LW、开题、PPT)
计算机源码社
Python项目大数据大数据pythonhadoop计算机毕业设计选题计算机毕业设计源码数据分析spark毕设
作者:计算机源码社个人简介:本人八年开发经验,擅长Java、Python、PHP、.NET、Node.js、Android、微信小程序、爬虫、大数据、机器学习等,大家有这一块的问题可以一起交流!学习资料、程序开发、技术解答、文档报告如需要源码,可以扫取文章下方二维码联系咨询Java项目微信小程序项目Android项目Python项目PHP项目ASP.NET项目Node.js项目选题推荐项目实战|p
- 两种方法判断Python的位数是32位还是64位
sanqima
Python编程电脑python开发语言
Python从1991年发布以来,凭借其简洁、清晰、易读的语法、丰富的标准库和第三方工具,在Web开发、自动化测试、人工智能、图形识别、机器学习等领域发展迅猛。 Python是一种胶水语言,通过Cython库与C/C++语言进行链接,通过Jython库与Java语言进行链接。 Python是跨平台的,可运行在多种操作系统上,包括但不限于Windows、Linux和macOS。这意味着用Py
- 使用最大边际相关性(MMR)选择示例:提高AI模型的多样性和相关性
aehrutktrjk
人工智能easyui前端python
使用最大边际相关性(MMR)选择示例:提高AI模型的多样性和相关性引言在机器学习和自然语言处理领域,选择合适的训练示例对模型性能至关重要。最大边际相关性(MaximalMarginalRelevance,MMR)是一种优秀的示例选择方法,它不仅考虑了示例与输入的相关性,还注重保持所选示例之间的多样性。本文将深入探讨如何使用MMR来选择示例,以提高AI模型的性能和泛化能力。什么是最大边际相关性(MM
- LangChain集成指南:如何利用多样化的AI提供商
aehrutktrjk
人工智能langchainpython
LangChain集成指南:如何利用多样化的AI提供商引言在人工智能和机器学习领域,LangChain已成为一个强大而灵活的框架,允许开发者轻松集成各种AI服务提供商。本文将深入探讨LangChain的集成能力,介绍如何利用不同的AI提供商来增强你的应用程序,并提供实用的代码示例。LangChain集成概览LangChain支持多种AI提供商的集成,这些集成可以分为两类:独立包集成:这些提供商有独
- 机器学习VS深度学习
nfgo
机器学习
机器学习(MachineLearning,ML)和深度学习(DeepLearning,DL)是人工智能(AI)的两个子领域,它们有许多相似之处,但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分:1.概念层面机器学习:是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习,常用的模型有决策树、支持向量机、线性回归等。深度学习:是机器学习的一个子领
- 大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏 租房推荐系统 58同城租房爬虫 房源推荐系统 房价预测系统 计算机毕业设计 机器学习 深度学习 人工智能
2401_84572577
程序员大数据hadoop人工智能
做了那么多年开发,自学了很多门编程语言,我很明白学习资源对于学一门新语言的重要性,这些年也收藏了不少的Python干货,对我来说这些东西确实已经用不到了,但对于准备自学Python的人来说,或许它就是一个宝藏,可以给你省去很多的时间和精力。别在网上瞎学了,我最近也做了一些资源的更新,只要你是我的粉丝,这期福利你都可拿走。我先来介绍一下这些东西怎么用,文末抱走。(1)Python所有方向的学习路线(
- 【机器学习与R语言】1-机器学习简介
苹果酱0567
面试题汇总与解析java中间件开发语言springboot后端
1.基本概念机器学习:发明算法将数据转化为智能行为数据挖掘VS机器学习:前者侧重寻找有价值的信息,后者侧重执行已知的任务。后者是前者的先期准备过程:数据——>抽象化——>一般化。或者:收集数据——推理数据——归纳数据——发现规律抽象化:训练:用一个特定模型来拟合数据集的过程用方程来拟合观测的数据:观测现象——数据呈现——模型建立。通过不同的格式来把信息概念化一般化:一般化:将抽象化的知识转换成可用
- Python前沿技术:机器学习与人工智能
4.0啊
Python人工智能python机器学习
Python前沿技术:机器学习与人工智能一、引言随着科技的飞速发展,机器学习和人工智能(AI)已经成为了计算机科学领域的热门话题。Python作为一门易学易用且功能强大的编程语言,已经成为了这两个领域的首选语言之一。本文将深入探讨Python在机器学习和人工智能领域的应用,以及一些前沿技术和工具。二、Python机器学习基础2.1机器学习概述机器学习是人工智能(AI)的一个关键子集,它的核心在于让
- chatgpt赋能python:如何在Python中计算平均值
tulingtest
ChatGptpythonchatgptnumpy计算机
如何在Python中计算平均值计算平均值是数据分析、统计和机器学习等许多领域中的常见任务。Python作为一门功能强大且易于学习的编程语言,为计算平均值提供了多种方法。在本文中,我们将介绍如何在Python中计算平均值。什么是平均值简单来说,平均值是一组数字的总和除以数字的数量。例如,对于数字序列1,3,5,7,9,平均值是(1+3+5+7+9)/5=5。平均值在数据分析中非常有用,因为它可以提供
- Python 初学者入门必知: Anaconda是什么?有什么作用?怎么使用?
懒大王爱吃狼
Python基础python开发语言python基础python学习anacondaanaconda安装python教程
初学者在学习Python时,经常看到的一个名字是Anaconda。究竟什么是Anaconda,为什么它如此受欢迎?在这篇文章中,我们将探讨Anaconda,了解Anaconda的从安装到使用的。Anaconda是一个免费开源的Python和R编程发行版,包含上千个适用于数据科学和机器学习的包。同时,配备了Spyder和Jupyternotebook等工具,初学者可以使用它们来学习Python,使用
- 每天五分钟玩转深度学习PyTorch:模型参数优化器torch.optim
幻风_huanfeng
深度学习框架pytorch深度学习pytorch人工智能神经网络机器学习优化算法
本文重点在机器学习或者深度学习中,我们需要通过修改参数使得损失函数最小化(或最大化),优化算法就是一种调整模型参数更新的策略。在pytorch中定义了优化器optim,我们可以使用它调用封装好的优化算法,然后传递给它神经网络模型参数,就可以对模型进行优化。本文是学习第6步(优化器),参考链接pytorch的学习路线随机梯度下降算法在深度学习和机器学习中,梯度下降算法是最常用的参数更新方法,它的公式
- 一切皆是映射:AI的去中心化:区块链技术的融合
AI大模型应用之禅
计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
一切皆是映射:AI的去中心化:区块链技术的融合作者:禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming关键词:AI,区块链,去中心化,智能合约,共识机制,数据安全,隐私保护,分布式账本技术,机器学习,数据隐私1.背景介绍1.1问题的由来随着人工智能(AI)技术的快速发展,其在各个领域的应用越来越广泛,从自动驾驶、智能医疗到金融服务,AI正在改变着我们的生活。
- 第五届核磁机器学习班(训练营:2023.6.5~6.17)
茗创科技
茗创科技专注于脑科学数据处理,涵盖(EEG/ERP,fMRI,结构像,DTI,ASL,FNIRS)等,欢迎留言讨论及转发推荐,也欢迎了解茗创科技的脑电课程,数据处理服务及脑科学工作站销售业务,可添加我们的工程师(微信号MCKJ-zhouyi或17373158786)咨询。★课程简介★基于血氧水平依赖的功能磁共振成像(fMRI)技术,利用其数据构建的功能性脑网络后,发现脑并不是一个单纯对外界刺激进行
- 如何有效的学习AI大模型?
Python程序员罗宾
学习人工智能语言模型自然语言处理架构
学习AI大模型是一个系统性的过程,涉及到多个学科的知识。以下是一些建议,帮助你更有效地学习AI大模型:基础知识储备:数学基础:学习线性代数、概率论、统计学和微积分等,这些是理解机器学习算法的数学基础。编程技能:掌握至少一种编程语言,如Python,因为大多数AI模型都是用Python实现的。理论学习:机器学习基础:了解监督学习、非监督学习、强化学习等基本概念。深度学习:学习神经网络的基本结构,如卷
- ASM系列六 利用TreeApi 添加和移除类成员
lijingyao8206
jvm动态代理ASM字节码技术TreeAPI
同生成的做法一样,添加和移除类成员只要去修改fields和methods中的元素即可。这里我们拿一个简单的类做例子,下面这个Task类,我们来移除isNeedRemove方法,并且添加一个int 类型的addedField属性。
package asm.core;
/**
* Created by yunshen.ljy on 2015/6/
- Springmvc-权限设计
bee1314
springWebjsp
万丈高楼平地起。
权限管理对于管理系统而言已经是标配中的标配了吧,对于我等俗人更是不能免俗。同时就目前的项目状况而言,我们还不需要那么高大上的开源的解决方案,如Spring Security,Shiro。小伙伴一致决定我们还是从基本的功能迭代起来吧。
目标:
1.实现权限的管理(CRUD)
2.实现部门管理 (CRUD)
3.实现人员的管理 (CRUD)
4.实现部门和权限
- 算法竞赛入门经典(第二版)第2章习题
CrazyMizzz
c算法
2.4.1 输出技巧
#include <stdio.h>
int
main()
{
int i, n;
scanf("%d", &n);
for (i = 1; i <= n; i++)
printf("%d\n", i);
return 0;
}
习题2-2 水仙花数(daffodil
- struts2中jsp自动跳转到Action
麦田的设计者
jspwebxmlstruts2自动跳转
1、在struts2的开发中,经常需要用户点击网页后就直接跳转到一个Action,执行Action里面的方法,利用mvc分层思想执行相应操作在界面上得到动态数据。毕竟用户不可能在地址栏里输入一个Action(不是专业人士)
2、<jsp:forward page="xxx.action" /> ,这个标签可以实现跳转,page的路径是相对地址,不同与jsp和j
- php 操作webservice实例
IT独行者
PHPwebservice
首先大家要简单了解了何谓webservice,接下来就做两个非常简单的例子,webservice还是逃不开server端与client端。我测试的环境为:apache2.2.11 php5.2.10做这个测试之前,要确认你的php配置文件中已经将soap扩展打开,即extension=php_soap.dll;
OK 现在我们来体验webservice
//server端 serve
- Windows下使用Vagrant安装linux系统
_wy_
windowsvagrant
准备工作:
下载安装 VirtualBox :https://www.virtualbox.org/
下载安装 Vagrant :http://www.vagrantup.com/
下载需要使用的 box :
官方提供的范例:http://files.vagrantup.com/precise32.box
还可以在 http://www.vagrantbox.es/
- 更改linux的文件拥有者及用户组(chown和chgrp)
无量
clinuxchgrpchown
本文(转)
http://blog.163.com/yanenshun@126/blog/static/128388169201203011157308/
http://ydlmlh.iteye.com/blog/1435157
一、基本使用:
使用chown命令可以修改文件或目录所属的用户:
命令
- linux下抓包工具
矮蛋蛋
linux
原文地址:
http://blog.chinaunix.net/uid-23670869-id-2610683.html
tcpdump -nn -vv -X udp port 8888
上面命令是抓取udp包、端口为8888
netstat -tln 命令是用来查看linux的端口使用情况
13 . 列出所有的网络连接
lsof -i
14. 列出所有tcp 网络连接信息
l
- 我觉得mybatis是垃圾!:“每一个用mybatis的男纸,你伤不起”
alafqq
mybatis
最近看了
每一个用mybatis的男纸,你伤不起
原文地址 :http://www.iteye.com/topic/1073938
发表一下个人看法。欢迎大神拍砖;
个人一直使用的是Ibatis框架,公司对其进行过小小的改良;
最近换了公司,要使用新的框架。听说mybatis不错;就对其进行了部分的研究;
发现多了一个mapper层;个人感觉就是个dao;
- 解决java数据交换之谜
百合不是茶
数据交换
交换两个数字的方法有以下三种 ,其中第一种最常用
/*
输出最小的一个数
*/
public class jiaohuan1 {
public static void main(String[] args) {
int a =4;
int b = 3;
if(a<b){
// 第一种交换方式
int tmep =
- 渐变显示
bijian1013
JavaScript
<style type="text/css">
#wxf {
FILTER: progid:DXImageTransform.Microsoft.Gradient(GradientType=0, StartColorStr=#ffffff, EndColorStr=#97FF98);
height: 25px;
}
</style>
- 探索JUnit4扩展:断言语法assertThat
bijian1013
java单元测试assertThat
一.概述
JUnit 设计的目的就是有效地抓住编程人员写代码的意图,然后快速检查他们的代码是否与他们的意图相匹配。 JUnit 发展至今,版本不停的翻新,但是所有版本都一致致力于解决一个问题,那就是如何发现编程人员的代码意图,并且如何使得编程人员更加容易地表达他们的代码意图。JUnit 4.4 也是为了如何能够
- 【Gson三】Gson解析{"data":{"IM":["MSN","QQ","Gtalk"]}}
bit1129
gson
如何把如下简单的JSON字符串反序列化为Java的POJO对象?
{"data":{"IM":["MSN","QQ","Gtalk"]}}
下面的POJO类Model无法完成正确的解析:
import com.google.gson.Gson;
- 【Kafka九】Kafka High Level API vs. Low Level API
bit1129
kafka
1. Kafka提供了两种Consumer API
High Level Consumer API
Low Level Consumer API(Kafka诡异的称之为Simple Consumer API,实际上非常复杂)
在选用哪种Consumer API时,首先要弄清楚这两种API的工作原理,能做什么不能做什么,能做的话怎么做的以及用的时候,有哪些可能的问题
- 在nginx中集成lua脚本:添加自定义Http头,封IP等
ronin47
nginx lua
Lua是一个可以嵌入到Nginx配置文件中的动态脚本语言,从而可以在Nginx请求处理的任何阶段执行各种Lua代码。刚开始我们只是用Lua 把请求路由到后端服务器,但是它对我们架构的作用超出了我们的预期。下面就讲讲我们所做的工作。 强制搜索引擎只索引mixlr.com
Google把子域名当作完全独立的网站,我们不希望爬虫抓取子域名的页面,降低我们的Page rank。
location /{
- java-归并排序
bylijinnan
java
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] a={20,1,3,8,5,9,4,25};
mergeSort(a,0,a.length-1);
System.out.println(Arrays.to
- Netty源码学习-CompositeChannelBuffer
bylijinnan
javanetty
CompositeChannelBuffer体现了Netty的“Transparent Zero Copy”
查看API(
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/buffer/package-summary.html#package_description)
可以看到,所谓“Transparent Zero Copy”是通
- Android中给Activity添加返回键
hotsunshine
Activity
// this need android:minSdkVersion="11"
getActionBar().setDisplayHomeAsUpEnabled(true);
@Override
public boolean onOptionsItemSelected(MenuItem item) {
- 静态页面传参
ctrain
静态
$(document).ready(function () {
var request = {
QueryString :
function (val) {
var uri = window.location.search;
var re = new RegExp("" + val + "=([^&?]*)", &
- Windows中查找某个目录下的所有文件中包含某个字符串的命令
daizj
windows查找某个目录下的所有文件包含某个字符串
findstr可以完成这个工作。
[html]
view plain
copy
>findstr /s /i "string" *.*
上面的命令表示,当前目录以及当前目录的所有子目录下的所有文件中查找"string&qu
- 改善程序代码质量的一些技巧
dcj3sjt126com
编程PHP重构
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点,程序你只写一次,但以后会无数次的阅读。当你第二天回头来看你的代码 时,你就要开始阅读它了。当你把代码拿给其他人看时,他必须阅读你的代码。因此,在编写时多花一点时间,你会在阅读它时节省大量的时间。让我们看一些基本的编程技巧: 尽量保持方法简短 尽管很多人都遵
- SharedPreferences对数据的存储
dcj3sjt126com
SharedPreferences简介: &nbs
- linux复习笔记之bash shell (2) bash基础
eksliang
bashbash shell
转载请出自出处:
http://eksliang.iteye.com/blog/2104329
1.影响显示结果的语系变量(locale)
1.1locale这个命令就是查看当前系统支持多少种语系,命令使用如下:
[root@localhost shell]# locale
LANG=en_US.UTF-8
LC_CTYPE="en_US.UTF-8"
- Android零碎知识总结
gqdy365
android
1、CopyOnWriteArrayList add(E) 和remove(int index)都是对新的数组进行修改和新增。所以在多线程操作时不会出现java.util.ConcurrentModificationException错误。
所以最后得出结论:CopyOnWriteArrayList适合使用在读操作远远大于写操作的场景里,比如缓存。发生修改时候做copy,新老版本分离,保证读的高
- HoverTree.Model.ArticleSelect类的作用
hvt
Web.netC#hovertreeasp.net
ArticleSelect类在命名空间HoverTree.Model中可以认为是文章查询条件类,用于存放查询文章时的条件,例如HvtId就是文章的id。HvtIsShow就是文章的显示属性,当为-1是,该条件不产生作用,当为0时,查询不公开显示的文章,当为1时查询公开显示的文章。HvtIsHome则为是否在首页显示。HoverTree系统源码完全开放,开发环境为Visual Studio 2013
- PHP 判断是否使用代理 PHP Proxy Detector
天梯梦
proxy
1. php 类
I found this class looking for something else actually but I remembered I needed some while ago something similar and I never found one. I'm sure it will help a lot of developers who try to
- apache的math库中的回归——regression(翻译)
lvdccyb
Mathapache
这个Math库,虽然不向weka那样专业的ML库,但是用户友好,易用。
多元线性回归,协方差和相关性(皮尔逊和斯皮尔曼),分布测试(假设检验,t,卡方,G),统计。
数学库中还包含,Cholesky,LU,SVD,QR,特征根分解,真不错。
基本覆盖了:线代,统计,矩阵,
最优化理论
曲线拟合
常微分方程
遗传算法(GA),
还有3维的运算。。。
- 基础数据结构和算法十三:Undirected Graphs (2)
sunwinner
Algorithm
Design pattern for graph processing.
Since we consider a large number of graph-processing algorithms, our initial design goal is to decouple our implementations from the graph representation
- 云计算平台最重要的五项技术
sumapp
云计算云平台智城云
云计算平台最重要的五项技术
1、云服务器
云服务器提供简单高效,处理能力可弹性伸缩的计算服务,支持国内领先的云计算技术和大规模分布存储技术,使您的系统更稳定、数据更安全、传输更快速、部署更灵活。
特性
机型丰富
通过高性能服务器虚拟化为云服务器,提供丰富配置类型虚拟机,极大简化数据存储、数据库搭建、web服务器搭建等工作;
仅需要几分钟,根据CP
- 《京东技术解密》有奖试读获奖名单公布
ITeye管理员
活动
ITeye携手博文视点举办的12月技术图书有奖试读活动已圆满结束,非常感谢广大用户对本次活动的关注与参与。
12月试读活动回顾:
http://webmaster.iteye.com/blog/2164754
本次技术图书试读活动获奖名单及相应作品如下:
一等奖(两名)
Microhardest:http://microhardest.ite

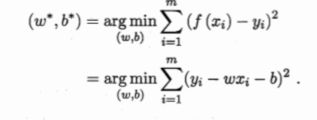
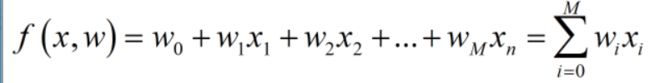


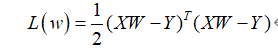
![]()
![]()
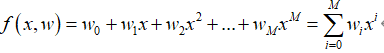
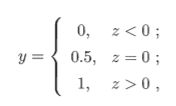
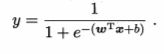


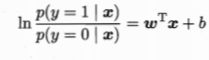
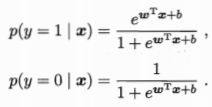


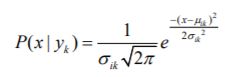
![]()
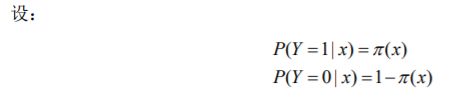
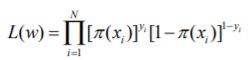
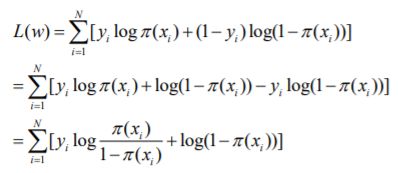

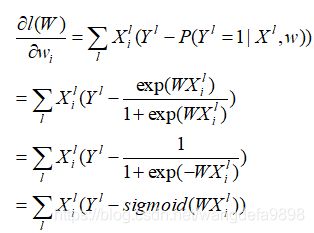
![]()