SVM的相关理解

SVM的相关理解

support vector machine，支持向量机，简称为SVM，通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，学习策略是间隔最大化，最终可转化为凸二次规划问题的求解。

1.SVM初解

1.1分类标准的起源：Logistic回归

​ 给定一些数据，他们分别属于两个不同的类，现在要找到一个线性分类器把这些数据分成两类。假如用x表示数据点，用y表示类别（y可以取1或者-1，分别代表两个不同的类，该分类标准起源于logistic回归），一个线性分类器的学习目标是在n维的数据空间找到一个超平面，这个超平面的方程可以表示为：（称为超平面的原因：样本的特征很可能是高维的，此时样本空间的划分就不是一条线了。）
$$w^{T}x+b=0$$

​ Logistic回归的目的是从特征学习出一个0/1分类模型，而这个模型是将特性的线性组合作为变量，由于自变量的取值范围是负无穷到正无穷。因此，使用logistic函数（或称作sigmoid函数）将自变量映射到(0,1)上，映射后的值被认为是属于y=1的概率。

假设函数
$$h_{\theta }=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$
​ 其中x是n维特征向量，函数g是logistic函数。（自我感觉有点类似于Z变换，将范围无穷的自变量映射到范围有限的因变量上）
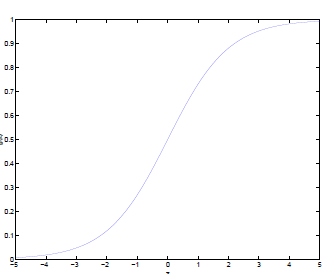
上述式子中，我们令$z={\theta }^{T}x$

则$g(z)=\frac{1}{1+e^{-z}}$的图像是：

则假设函数就是特征属于$y=1$的概率
$$\begin{gathered} P(y=1|x;\theta )=h_{\theta }(x) \\ P(y=0|x;\theta )=1-h_{\theta }(x) \end{gathered}$$
​ 从而，当我们要判别一个新来的特征属于哪一类时，只需要求$h_{\theta }(x)$即可，若$h_{\theta }(x)$大于0.5就是$y=1$的一类，反之为$y=0$的一类。

​ 此外，$h_{\theta }(x)$只和${\theta }^{T}x$有关，那么${\theta }^{T}x>0$,那么$h_{\theta }(x)>0.5$,真实的类别决定权还是在于${\theta }^{T}x$。再者，当${\theta }^{T}x>>0$时，$h_{\theta }(x)=1$，反之，$h_{\theta }(x)=0$。如果我们只从${\theta }^{T}x$出发，希望模型达到的目标就是让训练数据中$y=1$的特征${\theta }^{T}x>>0$,而$y=0$的特征${\theta }^{T}x<<0$。Logistic回归就是要学习得到$\theta$，使得正例的特征值远大于0，负例的特征值远小于0，而且要在全部的训练实例上达到这个目标。

​ 接下来，尝试把logistic回归做个变形。首先，将使用的结果标签替换为$y=0,y=1$替换为$y=-1,y=1$，然后将${\theta }^{T}x={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdot \cdot \cdot +{\theta }_n{x}_n(x_0=1)$中的${\theta }_0$替换成为$b$，最后将${\theta }_1{x}_1+{\theta }_2{x}_2+\cdot \cdot \cdot +{\theta }_n{x}_n$替换成$w_1{x}_1+w_2{x}_2+\cdot \cdot \cdot +w_n{x}_n$即$w^{T}x$。如此，则有了${\theta }^{T}x=w^{T}x+b$。也就是说除了$y$由$y=1$变为$y=-1$外，线性分类函数与logistic回归的形式化表示$h_{\theta }=g({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$没有区别。

​ 关于为什么将二分类的标签定为-1和1

1. ​ 对于二类问题，因为y只取两个值，这两个是可以任意取的，只要是取两个值就行；
2. 支持向量机去求解二类问题，目标是求一个特征空间的超平面，而超平面分开的两类对应于超平面的函数值的符号是刚好相反的；
3. 基于上述两种考虑，为了使问题足够简单，我们取y的值为1和-1；
4. 在取定分类标签y为-1和1之后，那么，一个平面正确分类样本数据，就相当于用这个平面计算的那个$yf(x)>0$；
5. 而且这样一来，$yf(x)$有明确的几何含义；
6. 二类问题的标签y是可以取任意两个值的，不管取怎样的值对于相同的样本点，只要分类相同，所有的y的不同取值都是等价的，之所以取某些特殊的值，只是因为这样一来计算会变得方便，理解变得容易。SVM中y取1或-1的历史原因是因为感知器最初的定义，实际取值可以任意，总能明确表示输入样本是否被误分，但是用+1、-1可以起码可以是问题描述简单化、式子表示简洁化、几何意义明确化。 举个例子，如要是取y为1和2，比如原来取-1的现在取1，原来取1的现在取2 ， 这样一来，分类正确的判定标准变为（y-1.5）*f（X)>0 ， 故取1和-1只是为了计算简单方便，没有实质变化，更非一定必须取一正一负。

1.2函数间隔与几何间隔

​ 在超平面$w^{T}x+b=0$确定的情况下，$|w^{T}x+b|$能够表示点$x$到距离超平面的远近，而通过观察$w^{T}x+b=0$的符号与类标记$y$的符号是否一致可判断分类是否正确，所以可以用$y(w^{T}x+b=0)$的正负来性判定分类的正确性。这里引入函数间隔的概念，定义函数间隔为$\check{\gamma }=y(w^{T}x+b)=yf(x)$

​ 而超平面$w^{T}x+b=0$关于T中所有样本点$(x_i,y_i)$的函数间隔最小值，为该超平面关于训练数据集$T$的函数间隔$\check{\gamma }=min(\check{{\gamma }_i})$。

​ 但是这样子的话，如果$w、b$成比例的变化，则函数间隔就会变成原来的两倍，但是超平面没有改变，所以只有函数间隔还不能完全准确地描述划分的优越性。

​ 事实上，我们可以对法向量$w$加些约束条件，从而引出真正定义点到超平面的距离------几何间隔。

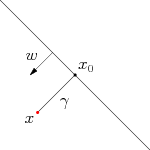
​ 假设一个点$x$,令其垂直投影到超平面上的对应点为$x_0$，$w$是垂直于超平面的一个向量，$\gamma$为样本$x$到平面的距离，如下图

​

​ 根据平面几何知识，有$x=x_0+\gamma \frac{w}{||w||}$其中$\frac{w}{||w||}$为单位向量，又由于$x_0$是超平面上的点，满足$f(x_0)=0$,代入超平面方程可得$w^T{x}_0=-b$。

​ 随机将$x=x_0+\gamma \frac{w}{||w||}$的两边同时乘以$w^T$,又知道$w^T{x}_0=-b$和$w^{T}w=||w|{|}^2$,即可算出$\gamma =\frac{w^{T}x+b}{||w||}=\frac{f(x)}{||w||}$,为了得到它的绝对值，由于我们知道$y$的类别的正负与其一致，则可得出几何间隔$\tilde{\gamma }=y\gamma =\frac{\check{\gamma }}{||w||}$。

​ 从上文可以看出，几何间隔就是函数间隔除以$||w||$，而且函数间隔$y(w^{T}x+b)=yf(x)$实际上就是$f(x)$的绝对值，是认为定义的一个间隔度量，集合间隔才是直观上点到超平面的距离。

1.3最大间隔分类器（SVM模型的推导）

​ 对一个数据集进行分类，当超平面离数据点的间隔越大，分类的确信度也就越大，所以为了使得分类的确信度尽可能高，需要使所选择的超平面能够最大化这个间隔值，这个间隔即下图中的$Gap$的一半。

通过上文的分析，可知所要找到的最大间隔分类超平面中的间隔指的是几何间隔，则可以定义目标函数：
$$max(\gamma )$$
由间隔的定义有：
$$\begin{array}{rl}\gamma & =\widetilde{{\gamma }_{+}}+\widetilde{{\gamma }_{-}}\\ & =\frac{\check{{\gamma }_{+}}+\check{{\gamma }_{-}}}{||w||}\\ & =\frac{f(x_{+})-f(x_{-})}{||w||}\\ & =\frac{x_{+}{w}^T-x_{-}{w}^T}{||w||}\end{array}$$
其中$x_{+}$和$x_{-}$分别表示两个正负支持向量，又因为$x_{+}$和$x_{-}$满足$y_i(w^T{x}_i+b)=1$，即
$$\{\begin{array}{l}{w}^T{x}_{+}+b=1\\ w^T{x}_{-}+b=-1\end{array}$$
推得：
$$\{\begin{array}{l}{w}^T{x}_{=}1-b\\ w^{T}x=-1-b\end{array}$$
则得到间隔$\gamma =\frac{1-b+1+b}{||w||}=\frac{2}{||w||}$

此时我们可以把目标函数化为$max(\frac{2}{||w||})$

又有约束条件，任意的训练集的点都应该属于已定义好的两个分类，即：
$$y_i(w^T{x}_i+b)\ge 1(i=1,2,\dots ,n)$$
最终可以得到支持向量机的基本型：
$$\begin{gathered} max(\frac{2}{||w||}) \\ s.t.y_i(w^T{x}_i+b)\ge 1(i=1,2,\dots ,n) \end{gathered}$$
对于上述基本型式子，可以使用现有的各种优化算法包来进行计算，但是可以通过数学推导进行更高效的计算；对基本型使用拉格朗日乘子法以及KKT条件，推导得到[具体推导过程]:https://blog.csdn.net/sinat_20177327/article/details/79729551?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.pc_relevant_is_cache&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.pc_relevant_is_cache

:
$$\begin{gathered} f(x)=w^T+b=\sum {\alpha }_i{y}_i{x}_i^{T}x+b \\ s.t.\{\begin{array}{l}{\alpha }_i\ge 0\\ y_{i}f(x_i)-1\ge 0\\ {\alpha }_i(y_{i}f(x_i)-1)=0\end{array} \end{gathered}$$
即对于任意训练样本$(x_i,y_i)$：

1. 若${\alpha }_i=0$,则它不影响模型的训练；
2. 若$\alpha >0$,则$y_{i}f(x_i)-1=0$，即该样本一定在边界上，是一个支持向量

这里可以发现支持向量机的特点：当训练完之后，大部分的样本是不需要保留的，最终模型只与支持向量有关。

2.SVM实例

from sklearn import svm
X = [[3, 0], [1, 1], [2,3]]
y = [0, 0, 1]
# 定义分类器，clf 意为 classifier，是分类器的传统命名
clf = svm.SVC(kernel = 'linear')  # .SVC（）就是 SVM 的方程，参数 kernel 为线性核函数
# 训练分类器
clf.fit(X, y)  # 调用分类器的 fit 函数建立模型（即计算出划分超平面，且所有相关属性都保存在了分类器 cls 里）
# 打印分类器 clf 的一系列参数
print(clf)
# 支持向量
print(clf.support_vectors_)
# 属于支持向量的点的 index
print(clf.support_)
# 在每一个类中有多少个点属于支持向量
print(clf.n_support_)
# 预测一个新的点
print(clf.predict([[2,0]]))

得到以下结果：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='linear', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)
[[1. 1.]
[2. 3.]]
[1 2]
[1 1]
[0]

导入iris数据集，再次进行测试：

from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris=load_iris()
x = iris['data']
y = iris['target']
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.6)
clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')
clf.fit(x_train, y_train.ravel())#kernel='linear'时，为线性核，C越大分类效果越好，但有可能会过拟合（defaul C=1）。
#kernel='rbf'时（default），为高斯核，gamma值越小，分类界面越连续；gamma值越大，分类界面越“散”，分类效果越好，但有可能会过拟合。
#decision_function_shape='ovr'时，为one v rest，即一个类别与其他类别进行划分，
#decision_function_shape='ovo'时，为one v one，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果。
print(clf.score(x_train, y_train))  # 精度
print(clf.score(x_test, y_test))

得到以下结果：

1.0
0.85

我们这里尝试对svm拟合的参数进行调整，观察结果，这里将C改为1：

clf = svm.SVC(C=1, kernel='rbf', gamma=20, decision_function_shape='ovr')
clf.fit(x_train, y_train.ravel())#kernel='linear'时，为线性核，C越大分类效果越好，但有可能会过拟合（defaul C=1）。
#kernel='rbf'时（default），为高斯核，gamma值越小，分类界面越连续；gamma值越大，分类界面越“散”，分类效果越好，但有可能会过拟合。
#decision_function_shape='ovr'时，为one v rest，即一个类别与其他类别进行划分，
#decision_function_shape='ovo'时，为one v one，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果。
print(clf.score(x_train, y_train))  # 精度
print(clf.score(x_test, y_test))

发现最终的测试集上的正确率有了些许的提高，但是运行速度似乎慢了不少

1.0
0.8666666666666667

将核方法改为线性，C值不变，发现对于测试集的拟合结果更好：

0.9777777777777777
1.0

参考文献

1.[支持向量机通俗导论（理解SVM的三层境界]:https://blog.csdn.net/v_july_v/article/details/7624837

2.[]:https://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html