Transformer

Transformer的整体架构为

图1

大框架分为了Encoder和Decoder，其中最为特殊的结构就是Multi-Head Attention，就是多头注意力机制。现在先讲注意力机制（self-attention）：

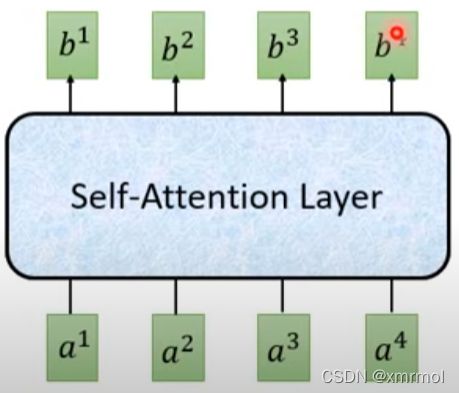
self-attention

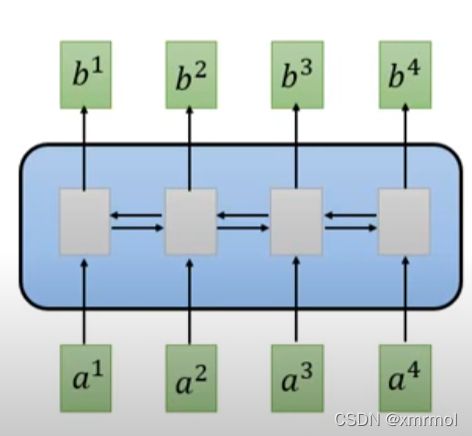
这个结构是处理序列信息，RNN处理序列是需要处理前面的信息得到特征，然后根据前面的特征再得到后面信息的特征，所以是有先后关系的，如果我们要得到t时刻的特征，就要计算前t-1时刻的特征。而self-attention不需要，它最关键的优点是可以同时得到这个序列中所有信息之间的特征。下图是RNN处理序列的结构：

下面是self-attention的时序结构：

具体做法：

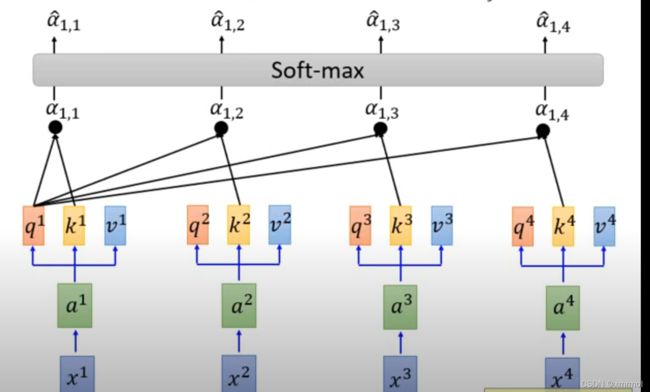
对于输入x，通过计算得到a，然后a通过三个矩阵(wq,wk,wv)计算得到q,k,v：
$$\begin{gathered} a^i=W{x}^i \\ {q}^i=W_q{a}^i{k}^i=W_k{a}^i{v}^i=W_v{a}^i \end{gathered}$$
（其实上面这个得到qkv的过程是需要注意的，在2017年论文中的self-attention的部分的qkv与这里定义不一样；文章里是先使q=k=v=x，然后将qkv输入模型，即模型输入为qkv，见图2（上面的计算是后来人通过Multi-Head Attention的结构做出的解释）。而这里模型输入是x，这是不一样的。对于Multi-Head Attention这两种其实是一回事，不用纠结）不重要

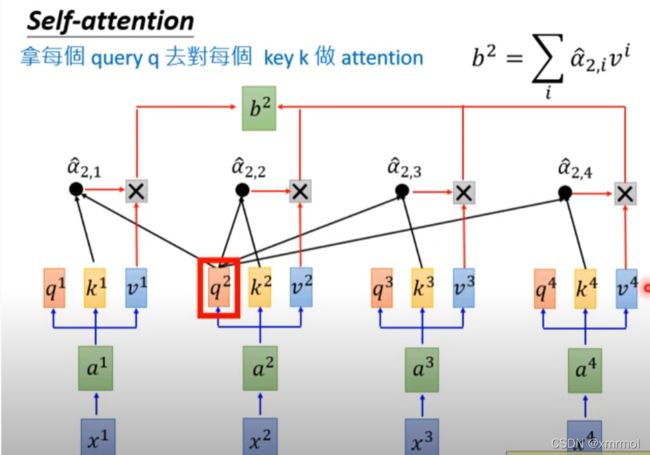
然后用每个输入的q对每个（包括自己）输入的k做attention，上图所展示的就是q1对每个的k做attention的示意图。这里使用点乘的方式计算attention，就是计算两个向量的相似度，如果两个向量点乘的值（内积）越大就说明向量的夹角越小，相似度越大，就是两个相关性越强，点乘得到的结果就越大。得到q11,a12,a13,a14，然后对这些值求softmax得到相关性的概率：
$$\begin{gathered} {\alpha }_{1,i}=q^1{k}^i/\sqrt{d} \\ {\alpha }_{1,i}=\exp {\alpha }_{1,i}/\sum _j\exp {\alpha }_{1,j} \end{gathered}$$
其中上式中的d是q和k的维度，因为每个信息的大小是不一样的，如果信息比较长的计算得到的值可能就比较大，所以为了消除这样的影响需要除以根号d。

然后使用softmax得到注意力比分分别乘以各自的v得到输出，这样的输出表示了其他信息对这条的信息的影响，按照比例改变这条信息的特征，影响越大比例越大。

使用q2计算同理，如下图所示：

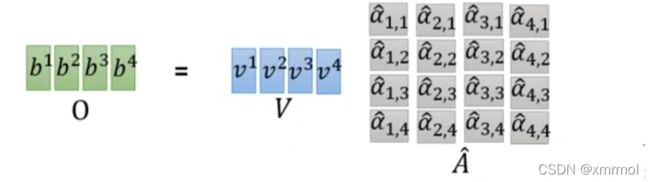
矩阵运算

所以可以同时得到所有信息的特征，总结得到self-attention的结构如图：

图2

演化：Multi-Head Attention

就是有多组self-attention，每个信息会生成多组qkv，而且他们之间计算attention是互相独立的，目的是使模型有不同的注意力。具体如下：

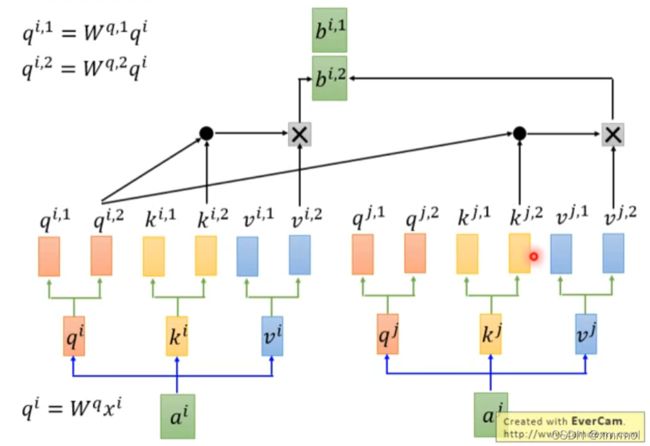
总结Multi-Head Attention的结构如下：

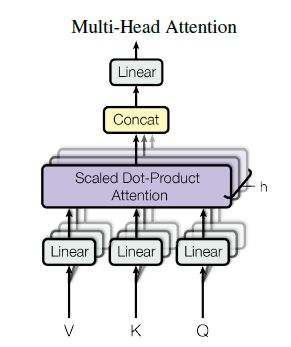
图3

Transformer

上面介绍了Transformer的Multi-Head Attention部分。下面介绍其余部分的结构和作用

Positional Encoding

上面的过程可以看到序列的顺序没有用了，因为他计算的时候是通过将一个信息和其他所有信息都做比较，所以顺序就没有体现出来。这里为了体现出信息的位置，加了Positional Encoding：

其中ei是加入了位置信息，这里是不需要训练，是人工设定的。

Add&Norm

之前使用的一直都是Batch Norm ，现在使用Layer Norm。

Batch Norm是对同一个特征，将所有batch上的数据进行归一化。

Layer Norm是对同一个batch，将所有特征数据进行归一化。

3D情况

原因：因为当batch中样本差异较大时，得到的均值和方差变动比较大（因为在训练过程中我们需要得到全局的均值和方差，然后在测试时才能对测试数据进行归一化），当全局的均值和方差遇到一个之前没学习过的很长的样本，就不准确了。

但是Layer Norm 不需要，他是对每个Layer做归一化，不需要全局的均值和方差，比较稳定。

Free Forward

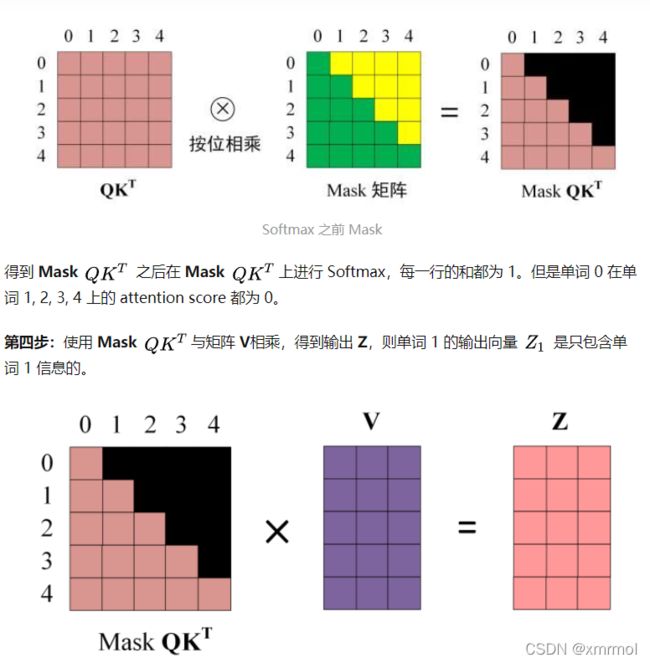
Masked Multi-Head Attention

这个就是在Multi-Head Attention中加入一个masked，**因为当处理第t时刻的信息时，我们是看不到t时刻以后的信息的，所以在做attention的时候需要屏蔽后面的信息，**这里加入了mask来屏蔽。这个就是self-attention结构图2中的 Mask(opt.) ，只不过在其他部分的Multi-Head Attention中不需要加mask，只在这个部分是需要mask的。计算步骤如下：

然后：

input

在Encoder中Multi-Head Attention输入是v=k=q=x，不过在Multi-Head Attention中存在全连接层对其进行变换；

在Decoder中Masked Multi-Head Attention输入是v=k=q=output，这里的output是Encoder的输出；

在Decoder中Multi-Head Attention输入是v=k=output，q=output_Masked，这里的output是Encoder的输出，output_Masked是上一层Masked Multi-Head Attention的输出。（这里就是比较output和output_Masked的相似度，然后根据得到的权重对output进行加权求和）

代码：https://github.com/tensorflow/tensor2tensor

ead Attention的输出。（这里就是比较output和output_Masked的相似度，然后根据得到的权重对output进行加权求和）

代码：https://github.com/tensorflow/tensor2tensor