上采样之反卷积操作
本文参考:
https://www.jianshu.com/p/b48bf190fe61
理解转置卷积 - 脂环 - 博客园
深度解析什么是转置卷积-电子发烧友网
https://blog.csdn.net/weixin_41620490/article/details/105885663
常用的下采样通过卷积和池化操作,不断缩小图像尺寸,减少矩阵的采样点数。
上采样通过反卷积或者插值操作,不断扩大图像尺寸,增加矩阵的采样点数。
卷积操作本身上是一种特征抽取,数据压缩的过程。
而反卷积是一种特殊的正向卷积,先按照一定的比例通过补0来扩大输入图像的尺寸,接着旋转卷积核,再进行正向卷积。但是该反卷积并不是卷积的逆过程,一旦卷积操作后,是无法通过反卷积还原回去的。反卷积更准确地讲应该是转置卷积。
如何理解转置?
首先从卷积操作讲起。
对于如上卷积操作,
输入input为4*4,kernel为3*3,stride为1,padding为0。则卷积后为:
数学推导时可以通过滑动kernel分别计算出每个值,但是计算机则是一次性计算出值。
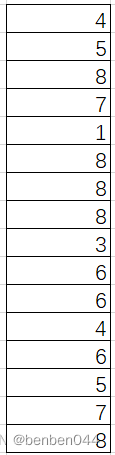
首先将输入转化成N*1,对于本input为16*1,如下:
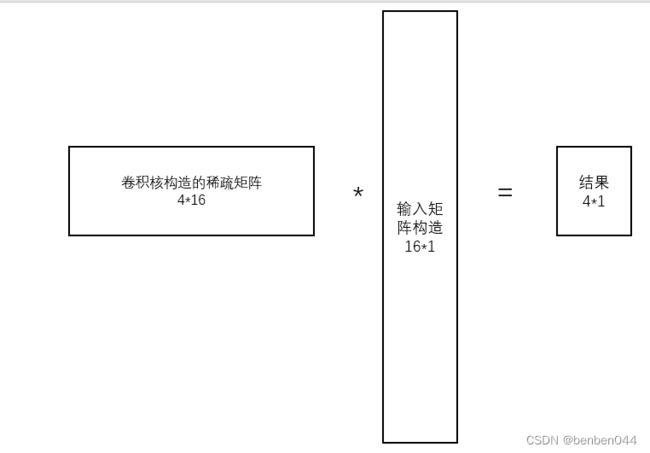
将卷积核转化为4*16的稀疏矩阵,如下图所示:
矩阵相乘得到4*1的结果的过程如下:
通过卷积核构造的4*16的稀疏矩阵,使得4*4 -> 16*1的输入直接得到了4*1 -> 2*2的结果。
而上采样则相反,我们希望2*2 -> 4*1的输入得到16*1 -> 4*4的结果,此时就需要使用到16*4的矩阵,从正向的4*16矩阵变为16*4的转置矩阵,故而得名转置矩阵。
如何计算输出大小?
首先给出卷积输出大小的计算公式:
转化后得到:
调换in和out的值,则得到转置卷积后的大小为:
pytorch如何计算转置卷积?
首先,卷积操作的代码如下:
import torch
import torch.nn as nn
model = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2,stride=1,padding=0)
x = torch.tensor([[[1.,2.,3.],[4.,5.,6.],[7.,8.,9.]]]).unsqueeze(0)
model.weight.data = torch.tensor([[[[1.,1.],[1.,1.]]]])
model.bias.data = torch.zeros(1)
print(model(x))输出结果为:
tensor([[[[12., 16.],
[24., 28.]]]], grad_fn=
转置卷积操作的代码如下:
import torch
import torch.nn as nn
model = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=3,stride=1,padding=0)
x = torch.tensor([[[12,16],[24,28]]], dtype=torch.float32).unsqueeze(0)
model.weight.data = torch.tensor([[[[1,1,1],[1,1,1],[1,1,1]]]], dtype=torch.float32)
model.bias.data = torch.zeros(1)
print(model(x))
输出结果为:
tensor([[[[12., 28., 28., 16.],
[36., 80., 80., 44.],
[36., 80., 80., 44.],
[24., 52., 52., 28.]]]], grad_fn=