深入理解反卷积

参考链接：https://www.zhihu.com/question/48279880/answer/525347615

参考链接：https://blog.csdn.net/itleaks/article/details/80336825

什么是反卷积？

• 上采样(Upsample)

在应用在计算机视觉的深度学习领域，由于输入图像通过卷积神经网络(CNN)提取特征后，输出的尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.:图像的语义分割)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)。

• 反卷积(Transposed Convolution)

上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：
反卷积是一种特殊的正向卷积，先按照一定的比例通过补 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

---

反卷积的数学推导

• 正向卷积的实现过程

假设输入图像 尺寸为 ，元素矩阵为：


卷积核 尺寸为 ，元素矩阵为：


步长 ，填充 ，即 ，
则按照卷积计算公式 ，输出图像 的尺寸为 。

• 用矩阵乘法描述卷积

把 的元素矩阵展开成一个列向量 ：


把输出图像 的元素矩阵展开成一个列向量 ：


对于输入的元素矩阵 和 输出的元素矩阵 ，用矩阵运算描述这个过程：


通过推导，我们可以得到稀疏矩阵 ：

反卷积的操作就是要对这个矩阵运算过程进行逆运算，即通过 和 得到 ，根据各个矩阵的尺寸大小，我们能很轻易的得到计算的过程，即为反卷积的操作：


但是，如果你代入数字计算会发现，反卷积的操作只是恢复了矩阵 的尺寸大小，并不能恢复 的每个元素值，本文最后会在 tensorflow 平台进行这个实验。

在此之前，我们先给出反卷积图像尺寸变化的公式。

• 反卷积的输入输出尺寸关系

在进行反卷积时，简单来说，大体上可分为以下两种情况：

Relationship 1：

此时反卷积的输入输出尺寸关系为：

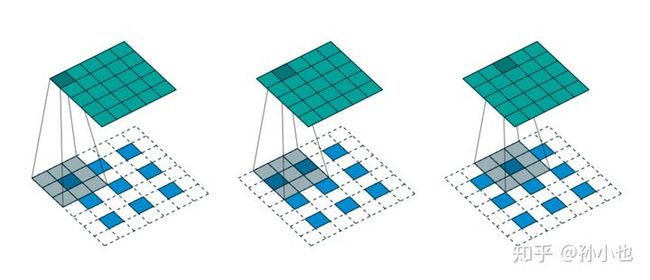
如上图所示，我们选择一个输入 尺寸为 ，卷积核 尺寸为 ，步长 ，填充 ，即 ，则输出 的尺寸为 。

Relationship 2：

此时反卷积的输入输出尺寸关系为：

如上图所示，我们选择一个输入 的尺寸为 ，卷积核 的尺寸为 ，步长 ，填充 ，即 ，则输出 的尺寸为 。

• 反卷积在 FCN 中的应用

在图像语义分割网络 FCN-32s 中，上采样反卷积操作的输入每张图像的尺寸是 ，我们希望进行一次上采样后能恢复成原始图像的尺寸 ，代入公式：


根据上式，我们可以得到一个关于 三者之间关系的等式：


通过实验，最终找出了最合适的一组数据：

---

在 tensorflow 中实现反卷积

• 反卷积的具体计算步骤

下面我们用一组实验更直观的解释一下在 tensorflow 中反卷积的过程：
我们令输入图像为：


卷积核为：


case 1
如果要使输出的尺寸是 ，步数 ，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input, 
                                        filter=kernel, 
                                        output_shape=[1,5,5,1], 
                                        strides=2, 
                                        padding='SAME')

当执行 transpose_conv 命令时，tensorflow 会先计算卷积类型、输入尺寸、步数和输出尺寸之间的关系是否成立，如果不成立，会直接提示错误，如果成立，执行如下操作：

1. 现根据步数 对输入的内部进行填充，这里 可以理解成输入放大的倍数，即在 的每个元素之间填充 ， 的个数 与 的关系为：


例如这里举例的 ，即在 的每个元素之间填 个 ：


因为卷积类型为 same，所以此时， 。

2. 接下来，用卷积核 对填充后的输入 进行步长 的正向卷积，根据正向卷积输出尺寸公式： 得到输出尺寸是 ，反卷积公式中我们给出的输出尺寸参数 也是为 ，两者相同，所以可以进行计算，结果为：


与 tensorflow 的运行结果相同。

case 2
我们将 case 1 中的输出尺寸 改成 ，其他参数均不变，tensorflow 中的命令为：

transpose_conv = tf.nn.conv2d_transpose(value=input,     
                                        filter=kernel,     
                                        output_shape=[1,6,6,1],   
                                        strides=2,         
                                        padding='SAME')

卷积类型是 same，我们首先在外围填充一圈 ：


这时发现，填充后的输入尺寸与 的卷积核卷积后的输出尺寸是 ，没有达到 的 ，这就需要继续填充 ，tensorflow 的计算规则是优先在左侧和上侧填充一排 ，填充后的输入变为：


接下来，再对这个填充后的输入与 的卷积核卷积，结果为：


与 tensorflow 的运行结果相同。
 

• 反卷积只能恢复尺寸，不能恢复数值

最后，我们要验证一下前文中提到的“如果你代入数字计算会发现，反卷积的操作只是恢复了矩阵 的尺寸大小，并不能恢复 的每个元素值”。

1. 正向卷积：

value = tf.reshape(tf.constant([[1., 2., 3.],              
                                [4., 5., 6.],                                   
                                [7., 8., 9.]]),                      
                   [1, 5, 5, 1])   

filter = tf.reshape(tf.constant([[1., 0.],                                    
                                 [0., 1.]]),                       
                    [2, 2, 1, 1])   

output = tf.nn.conv2d(value, filter, [1, 2, 2, 1], 'SAME')

卷积的结果是：


2. 我们用和正向卷积完全相同的参数对这个结果进行反卷积：

input = tf.reshape(tf.constant([[6., 8., 3.],            
                                [12., 14., 6.],         
                                [7., 8., 9.]]),        
                   [1, 3, 3, 1])    

kernel = tf.reshape(tf.constant([[1., 0.],       
                                 [0., 1.]]),        
                    [2, 2, 1, 1])   

output = tf.nn.conv2d_transpose(value=input,   
                                filter=kernel,  
                                output_shape=[1, 3, 3, 1],   
                                strides=[1, 2, 2, 1],    
                                padding='SAME')

卷积的结果是：


可见，反卷积不能恢复数值，而且，在当 时，即便使用完全相同的参数进行转置卷积，输入的尺寸也不能恢复。

 

 

反卷积（Deconvolution）的概念第一次出现是Zeiler在2010年发表的论文Deconvolutional networks中，但是并没有指定反卷积这个名字，反卷积这个术语正式的使用是在其之后的工作中(Adaptive deconvolutional networks for mid and high level feature learning)。随着反卷积在神经网络可视化上的成功应用，其被越来越多的工作所采纳比如：场景分割、生成模型等。其中反卷积（Deconvolution）也有很多其他的叫法，比如：Transposed Convolution，Fractional Strided Convolution等等。

这篇文章的目的主要有两方面：
1. 解释卷积层和反卷积层之间的关系；
2. 弄清楚反卷积层输入特征大小和输出特征大小之间的关系。

## 卷积层

卷积层大家应该都很熟悉了,为了方便说明，定义如下：

 

    我们再把4×4的输入特征展成[16,1]的矩阵X ,那么Y = CX则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是，在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的，因为这个转换会存在很多无用的0乘操作，Caffe中具体实现卷积计算的方法可参考Implementing convolution as a matrix multiplication。

    通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵C相乘，那么 我们很容易得到卷积层的反向传播就是和C的转置相乘。

反卷积和卷积的关系

 

Fractionally Strided Convolution

注意：计算padding按规则补0时，统一按照padding=‘SAME’、步长为1*1的方式来计算。