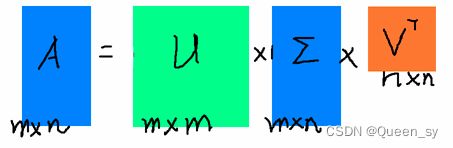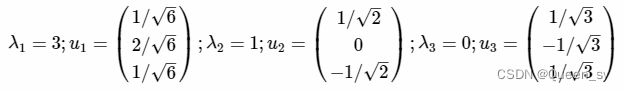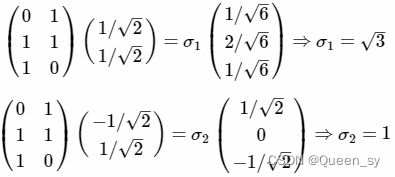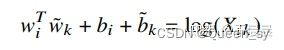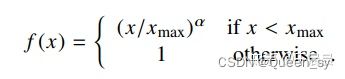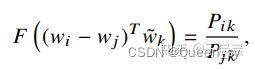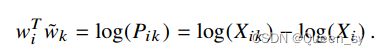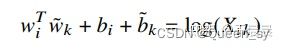【深度学习】词表示

目录

词表示

基于矩阵奇异值分解的词表示

基本思想：

语料

矩阵的奇异值分解(SVD)

基于神经网络的词表示

word2vec

Word Embedding

基于全局共现信息的词表示

共现概率矩阵

模型glove

模型动机

---

词表示

基于矩阵奇异值分解的词表示

基本思想：

利用SVD方法对共现矩阵进行分解，这种方法可以看作：对频率矩阵进行降噪和降维处理，并从中挖掘出词汇的潜在含义。

X=USVT

利用A乘以A的转置得到

m*m的矩阵，对这个矩阵进行特征值分解，得到的m个特征向量张成的m*m矩阵就是U矩阵。

词向量：从矩阵U中选取前k列，（列是特征向量）

U ：词表大小*k

特点：通过SVD得到了word的稠密矩阵，

1】语义相近的词在向量空间相近，甚至一定程度上可以反应词间的线性关系？

缺点：

1】需要事先构建好词共现矩阵，随新的语料的加入和新词的加入，词贡献矩阵是不断变化的，需要重新矩阵分解

2】绝大部分词不会共现，矩阵过于稀疏

3】矩阵维度高，10的6次幂*10的六次幂

4】训练是计算复杂度是O(|V|的3次方)

语料

NlP处理基本思路

1.获取预料

预料是nlp研究的内容，通常使用文本集合作为语料库，预料的来源分为3种：(1)已有的预料----积累的文档。(2)下载现有的语料---搜狗语料，人民日报语料等。(3)使用爬虫抓取。

2.语料的预处理

2.1 语料清洗：人工去重，对齐，标注或者规则提取内容，根据词性和命名实体提取

2.2 分词：将文本分成词语。(基于字符串匹配的分词方法，基于理解的分词方法，基于统计的分词方法，基于规则的分词方法)

2.3 词性标注：在情感分析或者知识推理中需要。(最大熵词性标注，基于统计最大概率输出词性，基于HMM的词性标注，基于规则)

2.4 去停用词：去掉对文本特征没有任何贡献作用的字词，比如标点符号，语气，人称等)

3.特征工程

将分词表示成计算机能够计算的类型(词向量)，常用的模型(词袋模型,tf-idf,one-hot,word2Vec)

4.特征选择

常见的特征选择方法(DF，MI,IG，CHI,WLLR,WFO)

5.模型训练

机器学习模型：KNN,SVM，Naive Bayes,K-Means,D-tree，GBDT等

深度学习模型：CNN,RNN，LSTM，seq2seq,fastText,TextCNN等

评价指标

Roc曲线，混淆矩阵，AUC曲线

模型部署

离线训练，线上部署。

在线训练，并持久化

矩阵的奇异值分解(SVD)

矩阵的本质可以是代表着一定维度空间上的线性变换。矩阵分解的本质是将原本m*n复杂的矩阵分解成对应的几个简单矩阵的乘积的形式。使得矩阵分析起来更加简单。

前面写过一篇博客讲的是矩阵的特征值分解，但是我们知道很多矩阵都是不能够进行特征值分解的。这种情况下，如果我们想通过矩阵分解的形式将原本比较复杂的矩阵问题分解成比较简单的矩阵相乘的形式，会对其进行奇异值分解。

简单回顾特征值分解

如果一个n*n矩阵A有n个特征值，并且这n个特征值所对应的n个特征向量线性无关，则矩阵A可以使用下式进行特征值分解：

其中，W是n个特征向量所张成的n*n维矩阵，而Sigma是一个对角矩阵，对角线上是矩阵A的n个特征值。

一般情况下，我们会将特征向量标准化（即令他们是单位向量），此时矩阵W的n个特征向量为标准正交基，所以会有，即，也就是说W为酉矩阵。所以特征值分解也可以写成

奇异值分解

奇异值分解并没有特征值分解那么苛刻的要求，对于任意一个m*n的矩阵A，可以对其进行如下奇异值分解：

其中，

• U是一个

m*m的矩阵；

• Sigma是一个

m*n的对角矩阵，主对角线上的元素成为奇异值；

• V是一个

n*n的矩阵，U与V都是酉矩阵，即组成它们的都是标准正交基。

如何奇异值分解？

1. 首先，利用A的转置乘以A会得到一个

n*n的矩阵，对这个矩阵进行特征值分解，得到的n个特征向量张成的n*n矩阵就是V矩阵，在这里我们将V中的每一个特征向量叫做A的右奇异向量；

1. 然后，利用A乘以A的转置得到

m*m的矩阵，对这个矩阵进行特征值分解，得到的m个特征向量张成的m*m矩阵就是U矩阵，在这里我们将每一个特征向量叫做左奇异向量；

1. 最后，利用下式求得每个

奇异值 

上述奇异值分解步骤的依据

在上面，我们说矩阵的特征向量组成的就是SVD的V矩阵，矩阵的特征向量组成的就是SVD的U矩阵，可以通过如下推导证明(以V矩阵为例)：

上式中我们还发现矩阵特征值矩阵等于A奇异值矩阵的平方，即，所以其实在第三步中我们求奇异值的方式其实也可以通过求出矩阵的特征值取平方根来求奇异值。

SVD求解实例

• 对于一个矩阵A:

• 首先计算出和

• 求出的特征值与特征向量

• 求出的特征值与特征向量

• 利用求得奇异值，我们会发现求得的结果与的结果相同;

• 最终得到A的奇异值分解为

基于神经网络的词表示

word2vec

Word Embedding

由于独热表示无法解决词之间相似性问题，这种表示很快就被词向量表示给替代了，这个时候聪明的你可能想到了在神经网络语言模型中出现的一个词向量 C(wi)，对的，这个 C(wi) 其实就是单词对应的 Word Embedding 值，也就是我们这节的核心——词向量。

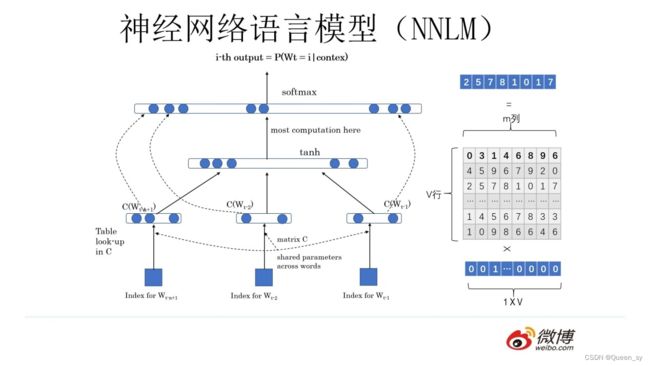
在神经网络语言模型中，我们并没有详细解释词向量是如何计算的，现在让我们重看神经网络语言模型的架构图：

上图所示有一个 V×m 的矩阵 Q，这个矩阵 Q 包含 V 行，V 代表词典大小，每一行的内容代表对应单词的 Word Embedding 值。

只不过 Q 的内容也是网络参数，需要学习获得，训练刚开始用随机值初始化矩阵 Q，当这个网络训练好之后，矩阵 Q 的内容被正确赋值，每一行代表一个单词对应的 Word embedding 值。词向量是神经网络语言模型的产物，

但是这个词向量有没有解决词之间的相似度问题呢？为了回答这个问题，我们可以看看词向量的计算过程：

[00010]⎡⎣⎢⎢⎢⎢⎢⎢1723410112456121817131925⎤⎦⎥⎥⎥⎥⎥⎥=[101219]公式(8)

通过上述词向量的计算，可以发现第 4 个词的词向量表示为 [101219]。

如果再次采用余弦相似度计算两个词之间的相似度，结果不再是 0 ，既可以一定程度上描述两个词之间的相似度。

下图给了网上找的几个例子，可以看出有些例子效果还是很不错的，一个单词表达成 Word Embedding 后，很容易找出语义相近的其它词汇。

四、Word2Vec 模型

2013 年最火的用语言模型做 Word Embedding 的工具是 Word2Vec ，后来又出了Glove（由于 Glove 和 Word2Vec 的作用类似，并对 BERT 的讲解没有什么帮助，之后不再多加叙述），Word2Vec是怎么工作的呢？看下图：

Word2Vec 的网络结构其实和神经网络语言模型（NNLM）是基本类似的，只是这个图长得清晰度差了点，看上去不像，其实它们是亲兄弟。不过这里需要指出：尽管网络结构相近，而且都是做语言模型任务，但是他们训练方法不太一样。

Word2Vec 有两种训练方法：

第一种叫 CBOW，核心思想是从一个句子里面把一个词抠掉，用这个词的上文和下文去预测被抠掉的这个词；

第二种叫做 Skip-gram，和 CBOW 正好反过来，输入某个单词，要求网络预测它的上下文单词。

而你回头看看，NNLM 是怎么训练的？是输入一个单词的上文，去预测这个单词。这是有显著差异的。

为什么 Word2Vec 这么处理？原因很简单，因为 Word2Vec 和 NNLM 不一样，NNLM 的主要任务是要学习一个解决语言模型任务的网络结构，语言模型就是要看到上文预测下文，而 Word Embedding只是 NNLM 无心插柳的一个副产品；但是 Word2Vec 目标不一样，它单纯就是要 Word Embedding 的，这是主产品，所以它完全可以随性地这么去训练网络。

为什么要讲 Word2Vec 呢？这里主要是要引出 CBOW 的训练方法，BERT 其实跟它有关系，后面会讲解它们之间的关系，当然它们的关系 BERT 作者没说，是我猜的，至于我猜的对不对，你看完这篇文章之后可以自行判断。

跳字模型（skip-gram）

两类方法对比：

	基于矩阵分解的词表示法	基于神经网络的词表示
	首先统计语料库中“词-文档’‘词-词”共线矩阵，然后矩阵分解获得低维词向量	通过神经网络使上下文窗口内频繁共现的单词对的表示接近
优点	利用全局统计信息	效果好、速度快
缺点	时间复杂度高、过度重视共线词频高的单词对	没有充分利用全局统计信息、过度重视共现词频高的单词对

基于全局共现信息的词表示

在传统上，实现word embedding有两种方式，Matrix Factorization Methods（矩阵分解方法）和Shallow Window-Based Methods（基于浅窗口的方法）

矩阵分解方法的代表是基于奇异值分解（SVD）的LSA算法，该方法对term-document矩阵（矩阵的每个元素为tf-idf）进行奇异值分解，从而得到term的向量表示和document的向量表示。此处使用的tf-idf主要还是term的全局统计特征。

基于浅窗口方法代表是word2vec，该算法可以分为skip-gram 和 continuous bag-of-words（CBOW）两类,但都是基于局部滑动窗口计算的。即，该方法利用了局部的上下文特征（local context）。

GloVe模型就是将这两中特征合并到一起的，既使用了语料库的全局统计（overall statistics）特征，也使用了局部的上下文特征（即滑动窗口）。为了做到这一点GloVe模型引入了Co-occurrence Probabilities Matrix（共现概率矩阵）。

共现概率矩阵

1. 什么是共现？

单词 i ii 出现在单词 j jj 的上下文中(论文给的环境是以为中心的左右10个单词区间)叫共现。

2. 什么是共现矩阵？

共现矩阵是单词对共现次数的统计表。我们可以通过大量的语料文本来构建一个共现统计矩阵。

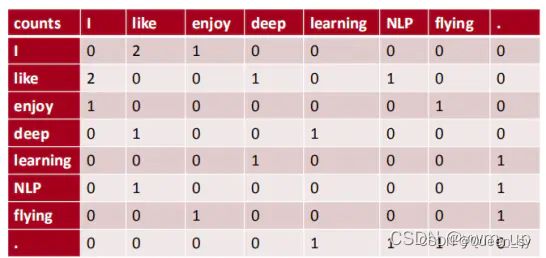
例如，有如下语料：

I like deep learning.I like NLP.I enjoy flying.

以窗半径为1来指定上下文环境，则共现矩阵就应该是:

共现矩阵有以下特点：

• 统计的是单词对在给定环境中的共现次数；所以它在一定程度上能表达词间的关系。
• 共现频次计数是针对整个语料库而不是一句或一段文档，具有全局统计特征。
• 共现矩阵它是对称的。

共现矩阵的生成使用中心词 + 滑动窗口进行统计。

行	每行对应一个词
列	每列表示一种不同的上下文
窗口大小为1	看前后一个词
元素	对应词汇和其上下文出现的次数

like

i 2

表示like出现在i上下文的次数=2次

3、符号介绍

X	共现矩阵
共现矩阵的元素X i j	词 j 出现在词 i 环境的次数
Xi​=∑k​Xik	任意词出现在环境的次数（即，共现矩阵第 i 行/列的和）
Pij​=P(j∣i)=Xi​Xij​​	词 j 出现在词i环境中的概率(这里以频率计算概率)，这一概率被称为词 i 和词 j 的共现概率。共现概率是指在给定的环境下出现(共现)某一个词的概率。注意：在给定语料库的情况下，我们是可以事先计算出任意一对单词的共现概率的。

Ratio=Pik/Pjk=词 k 出现在词 i 环境中的概率 / 词 k 出现在词 j 环境中的概率,也就是说如果一个词k和i共现的概率（ki相关）和词k和i共现的概率都很大，那么ij很有可能相关。

Ratio=Pik/Pjk	jk相关	jk不相关
ik相关	比值 1	大
ik不i相关	小	1

接下来阐述为啥作者要提共现概率和共现概率比这一概念。下面是论文中给的一组数据：

 

先看一下第一行数据，以ice为中心词的环境中出现solid固体的概率是大于gas、fashion而且小于water的，这是很合理的，对吧，因为现实语言使用习惯就是这样的。同理可以解释第二行数据。我们来重点考虑第三行数据：共现概率比。我们把共现概率相比，我们发现：

1.看第三行第一列：当ice的语境下共现solid的概率应该很大，当stream的语境下共现solid的概率应当很小，那么比值就>1。

2.看第三行第二列：当ice的语境下共现gas的概率应该很小，当stream的语境下共现gas的概率应当很大，那么比值就

3.看第三行第三列：当ice的语境下共现water的概率应该很大，当stream的语境下共现water的概率也应当很大，那么比值就近似=1。

4.看第三行第四列：当ice的语境下共现fashion的概率应该很小，当stream的语境下共现fashion的概率也应当很小，那么比值也是近似=1。

因为作者发现用共现概率比也可以很好的体现3个单词间的关联(因为共现概率比符合常理)，所以glove作者就大胆猜想，如果能将3个单词的词向量经过某种计算可以表达共现概率比就好了(glove思想)。如果可以的话，那么这样的词向量就与共现矩阵有着一致性，可以体现词间的关系。

模型glove

模型动机

模型

GloVe算法原理及简单使用

 构建词向量（WOrd Vector）和共现矩阵（Co-ocurrence Matrix）之间的近似关系

其中，wiT​ 和 w~j​ 是我们最终要求解的词向量，bi​ 和 b~j​ 分别是两个词向量的 bias term。

为什么要这样做的一个重要假设是：假设我们已经得到了词向量，如果我们使用词向量 vi​、vj​、vk​ 通过某种函数计算得到ratioi,j,k​，能够同样得到这样的规律的话，就意味着我们的词向量具备与共现矩阵很好的一致性，也就是说我们的词向量中蕴含了共现矩阵所蕴含的信息，而共现矩阵中所蕴含的信息就是在一个语料中某两个词语相关性的信息。

GloVe目标函数-构造 loss function

。

图17：GloVe目标函数

上图中f(Xijf(Xij是权重系数。权重系数应当遵循下面三个原则：

1. f(0)=0f(0)=0。
2. f(x)递增，以保证罕见的组合不会给与过多的权重。
3. 对于较大的x值，f(X)应该比较小，以保证频繁出现的组合不会给过多的权重。

有了上面三个原则，于是设计出了以下的权重函数，如图图18，其函数图像如图图19：

图18：GloVe目标函数的权重函数

GloVe目标函数的权重函数的函数图像

图19：GloVe目标函数的权重函数的函数图像

图19中权重函数的α=3/4α=3/4。xmaxxmax依赖于数据集，论文作者选取的xmax=100xmax=100，同时实验中发现α=3/4α=3/4效果好于α=1α=1，这与word2vec的选取3/4似乎有所巧合。

最终，我们训练得到了一个单词的向量表示ww和上下文向量w~w~。最终的向量也是使用了一个trick，将二者相加，作为单词的向量,实验表明，二者相加效果对比单独使用，略有提升。

至此，GloVe的原理推导完了。其实，也不能叫做推导，作者在论文里也只是说明这个损失函数怎么一步步得出来的。

公式推导

上面的讨论告诉我们，单词的词向量（word vector）学习应该跟词共现概率的比率有关，而不是他们的概率本身。注意到比率Pik/PjkPik/Pjk依赖于i,j,ki,j,k，最一般的形式如下图图10。

图10：词向量推导最一般的形式

其中，w∈Rdw∈Rd是词向量，w~∈Rdw~∈Rd是独立的上下文词向量。如果大家看过word2vec的话，此处的w就类似于最终一个词的表示，就是300维的词向量。 w~w~上下文的词向量，也是一个向量，跟ww同维度。首先，我们希望词向量的信息表正在比例Pik/PjkPik/Pjk里。词向量，内部是线性结构，这里希望更简洁的表示，所以这里做了一个相减来表示。不要问为什么要相减，这里面的很多推导都是比较跟着感觉走。就是这样子的。于是得到了下图图11的公式。

图11：公式的简单变形

主意右边是一个数字，左侧是向量。为了避免我们的网络，比如神经网络，关注到无用的东西。这里进行F里面的两个向量相乘。得到了下图图12中的公式。

图12：公式的简单变形

可以注意到词共现矩阵中，词和词的上下文词汇是任意的，我们自由的互换他们的位置。也就是我们互换w↔w~w↔w~，也可以互换 X↔XTX↔XT。为了满足这个条件，需要做以下两步操作。

第一步，我们的目标是要图12的公式满足同态（homomorphism）。至于什么是同态，笔者不太熟悉。可以看下图图13。假定我们认为满足下图图13的公式就是满足了同态性，满足了上述需求。

图13：公式要满足的条件，同态性

对比上图图12的公式，我们可以得到下图图14。

图14：对比图13得到

对于图13的公式，F是指数函数，F=exp，这一点应该很容易想到，因为图13中，两个变量的相减经过函数F等于两个变量经过函数F之后相除，显然是一个指数函数。于是有了图15。

图15：图13公式的一个解

第二步，注意到，图15中改变i和k的位置，会改变公式的对称性。所以为了保证对称性，为w~kw~k添加偏置b~kb~k。如下图图16。

图16：修正对称性后的公式

到目前为止，我们从图10的公式推导到了图16的公式，也就是我们训练最终的词向量要满足图16的公式。于是我们可以定义我们的目标函数（或者叫损失函数）如下：

J′=∑i,j=1V(wTiw~j+bi+b~j−logXij)J′=∑i,j=1V(wiTw~j+bi+b~j−logXij)

其中V是单词的总个数。但是上述目标函数还有一个问题，就是无论单词i和单词k之间出现的频率多少，都作为一个样本进行训练。那么对于那么单词i和单词k之间不常见的组合，或偶尔出现的组合，也进行拟合，其实这些拟合的是一些噪声，这显然不利于模型的鲁棒性/健壮性（robust）。怎么办呢？最简单的办法就来了，让那些出现次数较少的组合权重低一些。于是变为了下图土17。

图17：GloVe目标函数

GloVe部分结果展示

具体的实验结果，我不在此处张贴了。总之，作者对比了其他结果，总体上好于word2vec。有兴趣看具体结果的可以看原始论文[1]。这里只是简单展示一点。对frog（青蛙）这个单词，求最相似的单词，得到了如图20的结果。可以看到图中都是青蛙之类的词汇，表明了结果的有效性。

图20：GloVe对词frog求最相似的词向量的结果图

下图图21是我自己加载了GloVe预训练的模型[6]得到的最相似的单词的结果。

图21：加载GloVe预训练模型，笔者对词frog求最相似的词向量的结果图

代码

Glove论文详解及代码分析

，glove-python

参考：

GloVe算法原理及简单使用 - 知乎 (zhihu.com)

GloVe(Global Vectors for Word Representation )(2020-08-27)_fuchengguo666的博客-CSDN博客

简单粗暴！一文理解Skip-Gram上下文的预测算法

NLP之---word2vec算法skip-gram原理详解_小小的天和蜗牛的博客-CSDN博客_skip-gram

2022-02-21：NlP处理基本思路 - 简书

00 预训练语言模型的前世今生（全文 24854 个词） - 二十三岁的有德 - 博客园