【深度学习】非极大值抑制Non-Maximum Suppression(NMS)一文搞定理论+多平台实现...
薰风说
Non-Maximum Suppression的翻译是非“极大值”抑制,而不是非“最大值”抑制。这就说明了这个算法的用处:找到局部极大值,并筛除(抑制)邻域内其余的值。
这是一个很基础的,简单高效且适用于一维到多维的常见算法。因为特别适合目标检测问题,所以一直沿用至今,随着目标检测研究的深入和要求的提高(eg:原来只想框方框,现在想框多边形框),NMS也延伸出了不少变体。
与此同时,因为其比较基础,简单高效,因此我们更应该掌握它的实现。
一、为何/何时/如何NMS? Why&When&How NMS?
非极大值抑制[1](Non-Maximum Suppression,NMS),顾名思义就是抑制不是极大值的元素,可以理解为局部最大搜索。
这个局部代表的是一个邻域,邻域的“维度”和“大小”都是可变的参数。
NMS在计算机视觉领域有着非常重要的应用,如视频目标跟踪、3D重建、目标识别以及纹理分析等。
1. 为何要用NMS Why NMS?
首先,目标检测与图像分类不同,图像分类往往只有一个输出,但目标检测的输出个数却是未知的。除了Ground-Truth(标注数据)训练,模型永远无法百分百确信自己要在一张图上预测多少物体。
所以目标检测问题的老大难问题之一就是如何提高召回率。召回率(Recall)是模型找到所有某类目标的能力(所有标注的真实边界框有多少被预测出来了)。检测时按照是否检出边界框与边界框是否存在,可以分为下表四种情况:
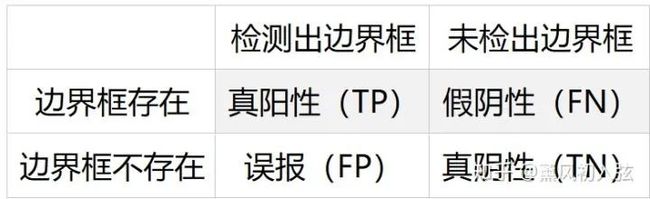
是所有某类物体中被检测出的概率,并由下式给出:
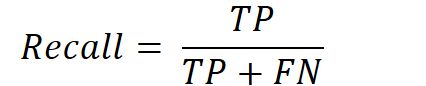
为了提高这个值,很直观的想法是“宁肯错杀一千,绝不放过一个”。因此在目标检测中,模型往往会提出远高于实际数量的区域提议(Region Proposal,SSD等one-stage的Anchor也可以看作一种区域提议)。
这就导致最后输出的边界框数量往往远大于实际数量,而这些模型的输出边界框往往是堆叠在一起的。因此,我们需要NMS从堆叠的边框中挑出最好的那个。
 目标检测中的NMS
目标检测中的NMS
2. 何时使用NMS?When NMS?
回顾我在R-CNN中提到的流程:
提议区域
提取特征
目标分类
回归边框
NMS使用在4. 回归边框之后,即所有的框已经被分类且精修了位置。且所有区域提议的预测结果已经由置信度与阈值初步筛选之后。
3. 如何非极大值抑制 How NMS?
一维简单例子
由于重点是二维(目标检测)的实现,因此一维只放出伪代码便于理解。
判断一维数组I[W]的元素I[i](2<=i<=W-1)是否为局部极大值,即大于其左邻元素I[i-1]和右邻元素I[i+1]
算法流程如下图所示:

算法流程3-5行判断当前元素是否大于其左邻与右邻元素,如符合条件,该元素即为极大值点。对于极大值点I[i],已知I[i]>I[i+1],故无需对i+1位置元素做进一步处理,直接跳至i+2位置,对应算法流程第12行。
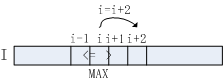
若元素I[i]不满足算法流程第3行判断条件,将其右邻I[i+1]作为极大值候选,对应算法流程第7行。采用单调递增的方式向右查找,直至找到满足I[i]>I[i+1]的元素,若i<=W-1,该点即为极大值点,对应算法流程第10-11行。
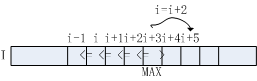
推广至目标检测
首先,根据之前分析确认NMS的前提,输入与输出。
使用前提
目标检测模型已经完成了整个前向计算,并给出所有可能的边界框(位置已精修)。
算法输入
算法对一幅图产生的所有的候选框,每个框有坐标与对应的打分(置信度)。
如一组5维数组:
每个组表明一个边框,组数是待处理边框数
4个数表示框的坐标:X_max,X_min,Y_max,Y_min
1个数表示对应分类下的置信度
注意:每次输入的不是一张图所有的边框,而是一张图中属于某个类的所有边框(因此极端情况下,若所有框的都被判断为背景类,则NMS不执行;反之若存在物体类边框,那么有多少类物体则分别执行多少次NMS)。
除此之外还有一个自行设置的参数:阈值 TH。
算法输出
输入的一个子集,同样是一组5维数组,表示筛选后的边界框。
算法流程
将所有的框按类别划分,并剔除背景类,因为无需NMS。
对每个物体类中的边界框(B_BOX),按照分类置信度降序排列。
在某一类中,选择置信度最高的边界框B_BOX1,将B_BOX1从输入列表中去除,并加入输出列表。
逐个计算B_BOX1与其余B_BOX2的交并比IoU,若IoU(B_BOX1,B_BOX2) > 阈值TH,则在输入去除B_BOX2。
重复步骤3~4,直到输入列表为空,完成一个物体类的遍历。
重复2~5,直到所有物体类的NMS处理完成。
输出列表,算法结束
二、算法实现
1. 交并比
交并比(Interp over Union)是目标检测NMS的依据,因此首先要搞懂交并比及其实现。
衡量边界框位置,常用交并比指标,交并比(Injection Over Union,IOU)发展于集合论的雅卡尔指数(Jaccard Index)[3],被用于计算真实边界框Bgt(数据集的标注)以及预测边界框Bp(模型预测结果)的重叠程度。
具体来说,它是两边界框相交部分面积与相并部分面积之比,如下所示:
Python(numpy)代码实现
import numpy as np
def compute_iou(box1, box2, wh=False):
"""
compute the iou of two boxes.
Args:
box1, box2: [xmin, ymin, xmax, ymax] (wh=False) or [xcenter, ycenter, w, h] (wh=True)
wh: the format of coordinate.
Return:
iou: iou of box1 and box2.
"""
if wh == False:
xmin1, ymin1, xmax1, ymax1 = box1
xmin2, ymin2, xmax2, ymax2 = box2
else:
xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
## 获取矩形框交集对应的左上角和右下角的坐标(interp)
xx1 = np.max([xmin1, xmin2])
yy1 = np.max([ymin1, ymin2])
xx2 = np.min([xmax1, xmax2])
yy2 = np.min([ymax1, ymax2])
## 计算两个矩形框面积
area1 = (xmax1-xmin1) * (ymax1-ymin1)
area2 = (xmax2-xmin2) * (ymax2-ymin2)
inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))#计算交集面积
iou = inter_area / (area1+area2-inter_area+1e-6)#计算交并比
return iou2. NMS的Python实现
从R-CNN开始,到fast R-CNN,faster R-CNN……都不难看到NMS的身影,且因为实现功能类似,基本的程序都是定型的,这里就分析Faster RCNN的NMS实现:
Python(numpy)代码实现
注意,这里的NMS是单类别的!多类别则只需要在外加一个for循环遍历每个种类即可
def py_cpu_nms(dets, thresh):
"""Pure Python NMS baseline."""
#dets某个类的框,x1、y1、x2、y2、以及置信度score
#eg:dets为[[x1,y1,x2,y2,score],[x1,y1,y2,score]……]]
# thresh是IoU的阈值
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
scores = dets[:, 4]
#每一个检测框的面积
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
#按照score置信度降序排序
order = scores.argsort()[::-1]
keep = [] #保留的结果框集合
while order.size > 0:
i = order[0]
keep.append(i) #保留该类剩余box中得分最高的一个
#得到相交区域,左上及右下
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
#计算相交的面积,不重叠时面积为0
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
#计算IoU:重叠面积 /(面积1+面积2-重叠面积)
ovr = inter / (areas[i] + areas[order[1:]] - inter)
#保留IoU小于阈值的box
inds = np.where(ovr <= thresh)[0]
order = order[inds + 1] #因为ovr数组的长度比order数组少一个,所以这里要将所有下标后移一位
return keepFaster R-CNN的MATLAB实现与python版实现一致,代码在这里:nms.m.另外,nms_multiclass.m是多类别nms,加了一层for循环对每类进行nms而已.
3. NMS的Pytorch实现
在Pytorch中,数据类型从numpy的数组变成了pytorch的tensor,因此具体的实现需要改变写法,但核心思路是不变的。
这里的实现参照了知乎大佬TeddyZhang的专栏
IoU计算的Pytorch源码为:(注意矩阵维度的变化)
# IOU计算
# 假设box1维度为[N,4] box2维度为[M,4]
def iou(self, box1, box2):
N = box1.size(0)
M = box2.size(0)
lt = torch.max( # 左上角的点
box1[:, :2].unsqueeze(1).expand(N, M, 2), # [N,2]->[N,1,2]->[N,M,2]
box2[:, :2].unsqueeze(0).expand(N, M, 2), # [M,2]->[1,M,2]->[N,M,2]
)
rb = torch.min(
box1[:, 2:].unsqueeze(1).expand(N, M, 2),
box2[:, 2:].unsqueeze(0).expand(N, M, 2),
)
wh = rb - lt # [N,M,2]
wh[wh < 0] = 0 # 两个box没有重叠区域
inter = wh[:,:,0] * wh[:,:,1] # [N,M]
area1 = (box1[:,2]-box1[:,0]) * (box1[:,3]-box1[:,1]) # (N,)
area2 = (box2[:,2]-box2[:,0]) * (box2[:,3]-box2[:,1]) # (M,)
area1 = area1.unsqueeze(1).expand(N,M) # (N,M)
area2 = area2.unsqueeze(0).expand(N,M) # (N,M)
iou = inter / (area1+area2-inter)
return iou其中:
torch.unsqueeze(1) 表示增加一个维度,增加位置为维度1
torch.squeeze(1) 表示减少一个维度
# NMS算法
# bboxes维度为[N,4],scores维度为[N,], 均为tensor
def nms(self, bboxes, scores, threshold=0.5):
x1 = bboxes[:,0]
y1 = bboxes[:,1]
x2 = bboxes[:,2]
y2 = bboxes[:,3]
areas = (x2-x1)*(y2-y1) # [N,] 每个bbox的面积
_, order = scores.sort(0, descending=True) # 降序排列
keep = []
while order.numel() > 0: # torch.numel()返回张量元素个数
if order.numel() == 1: # 保留框只剩一个
i = order.item()
keep.append(i)
break
else:
i = order[0].item() # 保留scores最大的那个框box[i]
keep.append(i)
# 计算box[i]与其余各框的IOU(思路很好)
xx1 = x1[order[1:]].clamp(min=x1[i]) # [N-1,]
yy1 = y1[order[1:]].clamp(min=y1[i])
xx2 = x2[order[1:]].clamp(max=x2[i])
yy2 = y2[order[1:]].clamp(max=y2[i])
inter = (xx2-xx1).clamp(min=0) * (yy2-yy1).clamp(min=0) # [N-1,]
iou = inter / (areas[i]+areas[order[1:]]-inter) # [N-1,]
idx = (iou <= threshold).nonzero().squeeze() # 注意此时idx为[N-1,] 而order为[N,]
if idx.numel() == 0:
break
order = order[idx+1] # 修补索引之间的差值
return torch.LongTensor(keep) # Pytorch的索引值为LongTensor其中:
torch.numel() 表示一个张量总元素的个数
torch.clamp(min, max) 设置上下限
tensor.item() 把tensor元素取出作为numpy数字
4. C++实现NMS
C++代码来自这个博客,真希望我也能有大佬们的码力233……毕竟搞工程早晚会掣肘于Python的
NMS和soft-nms算法 - outthinker - 博客园 www.cnblogs.com
程序整体思路:
先将box中的数据分别存入x1,y1,x2,y2,s中,分别为坐标和置信度,算出每个框的面积,存入area,基于置信度s,从小到达进行排序,做一个while循环,取出置信度最高的,即排序后的最后一个,然后将该框进行保留,存入pick中,然后和其他所有的框进行比对,大于规定阈值就将别的框去掉,并将该置信度最高的框和所有比对过程,大于阈值的框存入suppress,for循环后,将I中满足suppress条件的置为空。直到I为空退出while。
static void sort(int n, const float* x, int* indices)
{
// 排序函数(降序排序),排序后进行交换的是indices中的数据
// n:排序总数// x:带排序数// indices:初始为0~n-1数目
int i, j;
for (i = 0; i < n; i++)
for (j = i + 1; j < n; j++)
{
if (x[indices[j]] > x[indices[i]])
{
//float x_tmp = x[i];
int index_tmp = indices[i];
//x[i] = x[j];
indices[i] = indices[j];
//x[j] = x_tmp;
indices[j] = index_tmp;
}
}
}
int nonMaximumSuppression(int numBoxes, const CvPoint *points,
const CvPoint *oppositePoints, const float *score,
float overlapThreshold,
int *numBoxesOut, CvPoint **pointsOut,
CvPoint **oppositePointsOut, float **scoreOut)
{
// numBoxes:窗口数目// points:窗口左上角坐标点// oppositePoints:窗口右下角坐标点
// score:窗口得分// overlapThreshold:重叠阈值控制// numBoxesOut:输出窗口数目
// pointsOut:输出窗口左上角坐标点// oppositePoints:输出窗口右下角坐标点
// scoreOut:输出窗口得分
int i, j, index;
float* box_area = (float*)malloc(numBoxes * sizeof(float)); // 定义窗口面积变量并分配空间
int* indices = (int*)malloc(numBoxes * sizeof(int)); // 定义窗口索引并分配空间
int* is_suppressed = (int*)malloc(numBoxes * sizeof(int)); // 定义是否抑制表标志并分配空间
// 初始化indices、is_supperssed、box_area信息
for (i = 0; i < numBoxes; i++)
{
indices[i] = i;
is_suppressed[i] = 0;
box_area[i] = (float)( (oppositePoints[i].x - points[i].x + 1) *
(oppositePoints[i].y - points[i].y + 1));
}
// 对输入窗口按照分数比值进行排序,排序后的编号放在indices中
sort(numBoxes, score, indices);
for (i = 0; i < numBoxes; i++) // 循环所有窗口
{
if (!is_suppressed[indices[i]]) // 判断窗口是否被抑制
{
for (j = i + 1; j < numBoxes; j++) // 循环当前窗口之后的窗口
{
if (!is_suppressed[indices[j]]) // 判断窗口是否被抑制
{
int x1max = max(points[indices[i]].x, points[indices[j]].x); // 求两个窗口左上角x坐标最大值
int x2min = min(oppositePoints[indices[i]].x, oppositePoints[indices[j]].x); // 求两个窗口右下角x坐标最小值
int y1max = max(points[indices[i]].y, points[indices[j]].y); // 求两个窗口左上角y坐标最大值
int y2min = min(oppositePoints[indices[i]].y, oppositePoints[indices[j]].y); // 求两个窗口右下角y坐标最小值
int overlapWidth = x2min - x1max + 1; // 计算两矩形重叠的宽度
int overlapHeight = y2min - y1max + 1; // 计算两矩形重叠的高度
if (overlapWidth > 0 && overlapHeight > 0)
{
float overlapPart = (overlapWidth * overlapHeight) / box_area[indices[j]]; // 计算重叠的比率
if (overlapPart > overlapThreshold) // 判断重叠比率是否超过重叠阈值
{
is_suppressed[indices[j]] = 1; // 将窗口j标记为抑制
}
}
}
}
}
}
*numBoxesOut = 0; // 初始化输出窗口数目0
for (i = 0; i < numBoxes; i++)
{
if (!is_suppressed[i]) (*numBoxesOut)++; // 统计输出窗口数目
}
*pointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint)); // 分配输出窗口左上角坐标空间
*oppositePointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint)); // 分配输出窗口右下角坐标空间
*scoreOut = (float *)malloc((*numBoxesOut) * sizeof(float)); // 分配输出窗口得分空间
index = 0;
for (i = 0; i < numBoxes; i++) // 遍历所有输入窗口
{
if (!is_suppressed[indices[i]]) // 将未发生抑制的窗口信息保存到输出信息中
{
(*pointsOut)[index].x = points[indices[i]].x;
(*pointsOut)[index].y = points[indices[i]].y;
(*oppositePointsOut)[index].x = oppositePoints[indices[i]].x;
(*oppositePointsOut)[index].y = oppositePoints[indices[i]].y;
(*scoreOut)[index] = score[indices[i]];
index++;
}
}
free(indices); // 释放indices空间
free(box_area); // 释放box_area空间
free(is_suppressed); // 释放is_suppressed空间
return LATENT_SVM_OK;
}
碎碎念&絮叨一下
作为一个半路出家的初学者(本科电子信息工程,跨保CS),对coding一直处于某种“焦虑”的状态。
比如我可以花时间看懂别人的实现,也能在这个基础上小修小补,但从头搭建一个程序总会让我有一种莫名的抵触情绪。
而我也认识到,如果我想在个行业做出点成果,那不仅仅是需要git clone,调包调参那么简单,我必须从头开始一点点实现。甚至深入到一些框架的底层另起炉灶才能实现自己大胆的想法。
我离能够随心所欲地实现自己想法还有多远呢……希望越早越好吧,如果有幸你能看到这里,又有些经验可以分享的话。能说给我听听吗?
参考文献
[1]Neubeck A , Gool L J V . Efficient Non-Maximum Suppression[C]// 18th International Conference on Pattern Recognition (ICPR 2006), 20-24 August 2006, Hong Kong, China. IEEE Computer Society, 2006.
往期精彩回顾
适合初学者入门人工智能的路线及资料下载机器学习及深度学习笔记等资料打印机器学习在线手册深度学习笔记专辑《统计学习方法》的代码复现专辑
AI基础下载机器学习的数学基础专辑
获取本站知识星球优惠券,复制链接直接打开:
https://t.zsxq.com/qFiUFMV
本站qq群704220115。
加入微信群请扫码: