【机器学习】3:Density Peaks聚类算法实现(局部密度聚类算法)
前言:密度峰聚类算法和DBSCAN聚类算法有相似的地方,两者都是基于密度的聚类方式。自己是在学习无监督学习过程中,无意间见到介绍这种聚类算法的文章,感觉密度峰聚类算法方法很新奇,操作也很简答,于是自己也动手写一下了。
–-----------------------------------------------------------------------------—------------------------------------------------
–-----------------------------------------------------------------------------—------------------------------------------------
聚类算法主要包括哪些算法?
主要包括:K-means,DBSCAN,Density Peaks聚类(局部密度聚类),层次聚类,谱聚类。若按照聚类的方式可划分成三类:第一类是类似于K-means,DBSCAN,Density Peaks聚类(局部密度聚类)的依据密度的聚类方式; 第二种是类似于层次聚类的依据树状结构的聚类方式; 第三种是类似于谱聚类的依据图谱结构的聚类方式。
–-----------------------------------------------------------------------------—------------------------------------------------
–-----------------------------------------------------------------------------—------------------------------------------------
什么是无监督学习?
- 无监督学习也是相对于有监督学习来说的,因为现实中遇到的大部分数据都是未标记的样本,要想通过有监督的学习就需要事先人为标注好样本标签,这个成本消耗、过程用时都很巨大,所以无监督学习就是使用无标签的样本找寻数据规律的一种方法
- 聚类算法就归属于机器学习领域下的无监督学习方法。
–-----------------------------------------------------------------------------—------------------------------------------------
无监督学习的目的是什么呢?
可以从庞大的样本集合中选出一些具有代表性的样本子集加以标注,再用于有监督学习-可以从无类别信息情况下,寻找表达样本集具有的特征
–-----------------------------------------------------------------------------—------------------------------------------------
–-----------------------------------------------------------------------------—------------------------------------------------
分类和聚类的区别是什么呢?
- 对于分类来说,在给定一个数据集,我们是事先已知这个数据集是有多少个种类的。比如一个班级要进行性别分类,我们就下意识清楚分为“男生”、“女生”两个类;该班又转入一个同学A,“男ta”就被分入“男生”类;
- 而对于聚类来说,给定一个数据集,我们初始并不知道这个数据集包含多少类,我们需要做的就是将该数据集依照某个“指标”,将相似指标的数据归纳在一起,形成不同的类;
- 分类是一个后续的过程,已知标签数据,再将测试样本分入同标签数据集中;聚类是不知道标签,将“相似指标”的数据强行“撸”在一起,形成各个类。
–-----------------------------------------------------------------------------—------------------------------------------------
一、基于局部密度聚类算法——Density Peaks
1、背景介绍
Density Peaks聚类算法是在2014年 6 月份,由**Alex Rodriguez 和 Alessandro Laio 在 Science 上发表了一篇名为《Clustering by fast search and find of density peaks》**的文章,这为聚类算法的设计提供了一种新的思路。
虽然这个算法从Science上发表后也受到争议——部分学者觉得这篇思想简单、操作方便的聚类算法还达不到能在Science上发表的水平,这可能只是部分学者的口舌之争吧。但值得一提的是,写出Density Peaks聚类算法的两位科学家都不是研究数学,也不是研究算法分析的,而是西班牙研究化学的科学家。论文主体中也引证了很多采用这个聚类算法实现像人脸识别当前热火的场景的结果,如有兴趣,大家可以自己去细究一下。
2、定义局部密度大小—— ρ i \rho_i ρi
Density Peaks聚类算法要是用文字描述是有一些费解的,我尽量用图解释一下:
下图是一个样本空间点的分布图,一共分布着28个点:
- 事先给定一个邻域半径 d c d_c dc,定义任意i、j两点的距离用 d i j d_{ij} dij表示;
- ρ i \rho_i ρi表示i点的密度大小,i点的密度大小是如何确定的呢——以i点为圆心,包含在半径大小为 d c d_c dc的圆内点的个数即为i点的密度大小(与DBSCAN密度确定方法相似);
- 数学公式如下右所示,即比较两点距离 d i j d_{ij} dij与领域半径 d c d_c dc的大小关系,小于表示在圆内,计数1,大于表示圆外,计数0,最后求和。
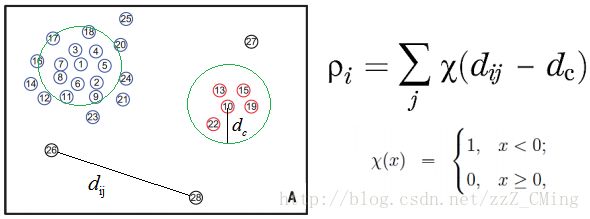
可得的结论: ρ i \rho_i ρi越大表示点i的局部密度越大,越有可能成为聚类中心。
3、定义聚类中心距离—— δ i \delta_i δi
密度峰聚类算法的巧妙之处:就是在于聚类中心距离 δ i \delta_i δi的选定。
根据局部密度的定义,我们可以计算出上图中每个点的密度,依照密度确定聚类中心距离 δ i \delta_i δi
1.首先将每个点的密度从大到小排列: ρ i \rho_i ρi > ρ j \rho_j ρj > ρ k \rho_k ρk > …;密度最大的点的聚类中心距离与其他点的聚类中心距离的确定方法是不一样的;
2.先确定密度最大的点的聚类中心距离–i点是密度最大的点,它的聚类中心距离 δ i \delta_i δi等于与i点最远的那个点n到点i的直线距离 d i n d_ { in } din;
3. 再确定其他点的聚类中心距离——其他点的聚类中心距离是等于在密度大于该点的点集合中,与该点距离最小的的那个距离。例如i、j、k的密度都比n点的密度大,且j点离n点最近,则n点的聚类中心距离等于 d j n d_{jn} djn
4. 依次确定所有的聚类中心距离 δ \delta δ
聚类中心距离 δ \delta δ的数学式如下:(虽然我觉得这个数学式表达的不是很贴切)
![]()
4、决策图确定聚类簇核心、簇边缘
Density Peaks聚类算法就是依据每个点的局部密度大小 ρ i \rho_i ρi、聚类中心距离 δ i \delta_i δi的数值,组合( ρ i \rho_i ρi, δ i \delta_i δi)投射到二维坐标系中。先上决策图:
![]()
(这里聚类中心距离经过归一化处理,将①号点的聚类中心距离 δ 1 , 27 \delta_{1,27} δ1,27定为1)
从B图中可以清楚的看出来:
分布在右上角区域的是聚类的核心点:周围密度很大,且没有其他核心点;
分布在靠近ρ轴的值是属于正常值:密度虽然大,但是周围有比它更合适作为核心点的点;
分布在靠近δ轴的值是属于噪声点:周围密度小,而且离其他点的距离还远。
现实意义就是:北京联合天津、廊坊等地构成帝都经济群,上海联合无锡、常州、苏州构成长江三角洲经济群,广州深圳形成珠三角经济群。北京、上海、广州深圳相当于聚类核心点,引领发展;天津虽然也是现代化城市,但是由于它离北京很近,更多的资源会流向聚类核心点北京,所以天津只能作为正常点。
5、Density Peaks聚类算法的意义
聚类算法中最困惑的地方就是选定K值等于多少才算合适,Density Peaks聚类算法给出了一种比较好的确定K值的方式:定义γi=ρi*δi,得到的乘积比较选取较大的K个点作为聚类中心。
源码:
注意:请修改第10、11行的设定参数
# -*- coding:utf-8 -*-
# -*- author:zzZ_CMing CSDN address:https://blog.csdn.net/zzZ_CMing
# -*- 2018/08/22;16:11
# -*- python3.5
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
min_distance = 4.6 # 邻域半径
points_number = 5 # 随机点个数
# 计算各点间距离、各点点密度(局部密度)大小
def get_point_density(datas,labers,min_distance,points_number):
# 将numpy.ndarray格式转为list格式,并定义元组大小
data = datas.tolist()
laber = labers.tolist()
distance_all = np.random.rand(points_number,points_number)
point_density = np.random.rand(points_number)
# 计算得到各点间距离
for i in range(points_number):
for n in range(points_number):
distance_all[i][n] = np.sqrt(np.square(data[i][0]-data[n][0])+np.square(data[i][1]-data[n][1]))
print('距离数组:\n',distance_all,'\n')
# 计算得到各点的点密度
for i in range(points_number):
x = 0
for n in range(points_number):
if distance_all[i][n] > 0 and distance_all[i][n]< min_distance:
x = x+1
point_density[i] = x
print('点密度数组:', point_density, '\n')
return distance_all, point_density
# 计算点密度最大的点的聚类中心距离
def get_max_distance(distance_all,point_density,laber):
point_density = point_density.tolist()
a = int(max(point_density))
# print('最大点密度',a,type(a))
b = laber[point_density.index(a)]
# print("最大点密度对应的索引:",b,type(b))
c = max(distance_all[b])
# print("最大点密度对应的聚类中心距离",c,type(c))
return c
# 计算得到各点的聚类中心距离
def get_each_distance(distance_all,point_density,data,laber):
nn = []
for i in range(len(point_density)):
aa = []
for n in range(len(point_density)):
if point_density[i] < point_density[n]:
aa.append(n)
# print("大于自身点密度的索引",aa,type(aa))
ll = get_min_distance(aa,i,distance_all, point_density,data,laber)
nn.append(ll)
return nn
# 获得:到点密度大于自身的最近点的距离
def get_min_distance(aa,i,distance_all, point_density,data,laber):
min_distance = []
"""
如果传入的aa为空,说明该点是点密度最大的点,该点的聚类中心距离计算方法与其他不同
"""
if aa != []:
for k in aa:
min_distance.append(distance_all[i][k])
# print('与上各点距离',min_distance,type(nn))
# print("最小距离:",min(min_distance),type(min(min_distance)),'\n')
return min(min_distance)
else:
max_distance = get_max_distance(distance_all, point_density, laber)
return max_distance
def get_picture(data,laber,points_number,point_density,nn):
# 创建Figure
fig = plt.figure()
# 用来正常显示中文标签
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
# 用来正常显示负号
matplotlib.rcParams['axes.unicode_minus'] = False
# 原始点的分布
ax1 = fig.add_subplot(211)
plt.scatter(data[:,0],data[:,1],c=laber)
plt.title(u'原始数据分布')
plt.sca(ax1)
for i in range(points_number):
plt.text(data[:,0][i],data[:,1][i],laber[i])
# 聚类后分布
ax2 = fig.add_subplot(212)
plt.scatter(point_density.tolist(),nn,c=laber)
plt.title(u'聚类后数据分布')
plt.sca(ax2)
for i in range(points_number):
plt.text(point_density[i],nn[i],laber[i])
plt.show()
def main():
# 随机生成点坐标
data, laber = ds.make_blobs(points_number, centers=points_number, random_state=0)
print('各点坐标:\n', data)
print('各点索引:', laber, '\n')
# 计算各点间距离、各点点密度(局部密度)大小
distance_all, point_density = get_point_density(data, laber, min_distance, points_number)
# 得到各点的聚类中心距离
nn = get_each_distance(distance_all, point_density, data, laber)
print('最后的各点点密度:', point_density.tolist())
print('最后的各点中心距离:', nn)
# 画图
get_picture(data, laber, points_number, point_density, nn)
"""
距离归一化:就把上面的nn改为:nn/max(nn)
"""
if __name__ == '__main__':
main()
结果展示:
1、由于随机生成的数据大多是分散的,所以得到的实验效果不是很理想;
2、有这方面需求的伙伴们可以自己做拓展——将随机数据生成改为引入自己在txt或excel中的数据做测试;
3、高维空间也是可以的,但时间复杂度和内存消耗我并没有估计,改进也留给你们了。
![]()
![]()
系列推荐:
【监督学习】1:KNN算法实现手写数字识别的三种方法
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
【无监督学习】1:K-means算法原理介绍,以及代码实现
【无监督学习】2:DBSCAN算法原理介绍,以及代码实现
【无监督学习】3:Density Peaks聚类算法(局部密度聚类)
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
【深度学习】1:感知器原理,以及多层感知器解决异或问题
【深度学习】2:BP神经网络的原理,以及异或问题的解决
【深度学习】3:BP神经网络识别MNIST数据集
【深度学习】4:BP神经网络+sklearn实现数字识别
【深度学习】5:CNN卷积神经网络原理、MNIST数据集识别
【深度学习】8:CNN卷积神经网络识别sklearn数据集(附源码)
【深度学习】6:RNN递归神经网络原理、MNIST数据集识别
【深度学习】7:Hopfield神经网络(DHNN)原理介绍
–-----------------------------------------------------------------------------—--------------------------------------------------------—----
TensorFlow框架简单介绍
–-----------------------------------------------------------------------------—--------------------------------------------------------—----