【建模算法】基于蚁群算法求解TSP问题(matlab求解)
【建模算法】基于蚁群算法求解TSP问题(matlab求解)
TSP (traveling salesman problem,旅行商问题)是典型的NP完全问题,即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长,到目前为止还未找到一个多项式时间的有效算法。本文探讨了使用matlab软件,基于蚁群算法求解TSP问题。
一、问题描述
本案例以31个城市为例,假定31个城市的位置坐标如表1所列。寻找出一条最短的遍历31个城市的路径。
| 城市编号 | X坐标 | Y坐标 | 城市编号 | X坐标 | Y坐标 |
|---|---|---|---|---|---|
| 1 | 1.304 | 2.312 | 17 | 3.918 | 2.179 |
| 2 | 3.639 | 1.315 | 18 | 4.061 | 2.37 |
| 3 | 4.177 | 2.244 | 19 | 3.78 | 2.212 |
| 4 | 3.712 | 1.399 | 20 | 3.676 | 2.578 |
| 5 | 3.488 | 1.535 | 21 | 4.029 | 2.838 |
| 6 | 3.326 | 1.556 | 22 | 4.263 | 2.931 |
| 7 | 3.238 | 1.229 | 23 | 3.429 | 1.908 |
| 8 | 4.196 | 1.044 | 24 | 3.507 | 2.376 |
| 9 | 4.312 | 0.79 | 25 | 3.394 | 2.643 |
| 10 | 4.386 | 0.57 | 26 | 3.439 | 3.201 |
| 11 | 3.007 | 1.97 | 27 | 2.935 | 3.24 |
| 12 | 2.562 | 1.756 | 28 | 3.14 | 3.55 |
| 13 | 2.788 | 1.491 | 29 | 2.545 | 2.357 |
| 14 | 2.381 | 1.676 | 30 | 2.778 | 2.826 |
| 15 | 1.332 | 0.695 | 31 | 2.37 | 2.975 |
| 16 | 3.715 | 1.678 |
二、蚁群算法基本思想
大自然中的真实蚂蚁是基本看不见东西的,而且单个蚂蚁的行为非常简单,它们寻找食物的行为带有随机性。但是由这些简单的个体所组成的蚁群却有着及其缜密的组织性,能够完成相对复杂的工作。蚂蚁能在其走过的路径上分泌一种叫做信息素的物质,并形成信息素轨迹。其它蚂蚁在运动过程中能够感知这种物质的存在和强度,并以此指导自己的运动路线,使之朝着信息素强度大的方向运动,这使得蚁群在食物源与蚁穴之间的最短路径上来去自如。蚁群算法就是受到蚁群这种行为的启发,而提出的一种启发式搜索算法。作为一种现代智能算法,蚁群算法不需要任何先验知识,最初只是随机地选择搜索路径,随着对解空间的了解,搜索更加具有规律性,并逐渐得到全局最优解。目前,蚁群算法已被成功地应用于求解旅行商问题、车辆调度问题以及指派问题等,并取得了较好的结果。
假设池塘的周围有两条道路,可由蚁穴通往食物源: L 1 L_1 L1={ABHDE}和 L 2 L_2 L2={ABCDE},其中为A蚁穴,E为食物源,BH和HD间的离为1m,BC和CD间的距离为0.5m,如下所示。
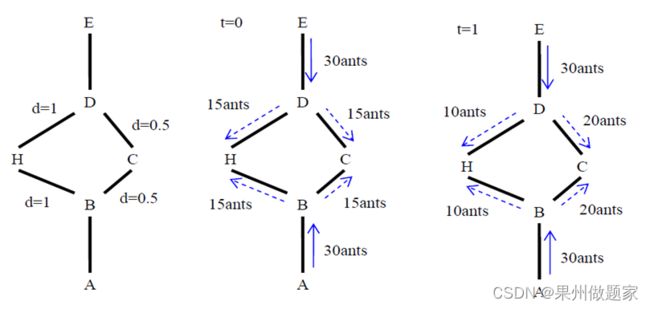
初始时刻(t=0),当30只蚂蚁分别同时走到分岔路口B和 D点时,要决定往哪个方向走。由于初始时刻时没有任何线索可以为蚂蚁提供选择路径的标准,假设它们就以相同的概率选择路径,因此,有15只蚂蚁走左边的路径BH 、DH ,另外15只蚂蚁走右边的路径BC 、DC ,这些蚂蚁在行进的过程中分别留下信息素。
假设蚂蚁都具有相同的速度(1m/s)和信息释放能力,则经过1s 后(t=1),从D 点出发的30只蚂蚁有15只到达了 H点,有15只蚂蚁经过C点到达了B点,同样,从B点出发的30只蚂蚁有15只到达了H点,有15只蚂蚁经过C点到达了D点。很显然,在相等的时间间隔内,路径DHB上共有15只蚂蚁经过并留下了信息素,路径DCB上却有30只蚂蚁经过并留下了信息素,其信息素浓度是DHB路径上的2倍。
因此,当30只蚂蚁分别回到A、E点重新选择路径时,就会以2倍于DHB的概率选择路径DCB,从而DCB上的蚂蚁数目变成了20只,这样,路径DCB上信息素很快得到了增强,其路径最短的优势也很快被蚁群发现。
综上,某条路径上走过的蚂蚁越多,则后来者选择该路径的概率越大,所以我们可以认为蚁群在毫无提示的前提条件下,正确地选择了最短路径,达到了最快觅食的目的,并且可以在周围环境变化的情况下,依靠信息素的变化迅速调整并找到新的最短路径。
三、蚁群算法数学模型
下面以旅行商问题(TSP)为例来更深入地介绍蚁群算法,并建立其数学模型。并假设:
(1)蚂蚁根据与城市间距离和路径上信息素含量有关的某一概率函数选择下一个需要访问的城市;
(2)每只蚂蚁在完成一次周游(指蚂蚁走完所有的城市)以前,不允许转到已访问的城市;
(3)蚂蚁在完成一次周游时,在每一条走过的边上释放信息素;
(4)蚂蚁留在边上的信息素会随着时间地推移不断挥发。
以上三种计算方式可根据不同的情况进行选取,它们之间的对比如下表所示:
| 方 式 | 蚁密系统 | 蚁量系统 | 蚁周系统 |
|---|---|---|---|
| 最 优 解 | 局部最优 | 局部最优 | 全局最优 |
| 收敛速度 | 慢 | 较快 | 快 |
| 算法效率 | 较低 | 较高 | 高 |
显然,蚁周系统使用的是全局信息,得到的解是全局最优解,且整个算法的收敛速度更快、算法效率更高。
四、蚁群算法实现
蚁群算法TSP实现的具体步骤如下:
Step 1:设置最大迭代次数iter_max,令初始值iter_max=0,初始化各参数;
Step 2:设蚁群规模为m ,并将m只蚂蚁随机放在n个顶点(城市)上;
Step 3:对每只蚂蚁k(k=1,2,…,m)根据式(3-1)计算转移概率 p i j k p_{ij}^k pijk,选择转移至下一个顶点(城市)j,将顶点(城市)j置于禁忌表 t a b u k tabu_k tabuk中;
Step 4:判断禁忌表 t a b u k tabu_k tabuk是否满。若为否,回到Step 3,否则,继续Step 4;
Step 5:按照(3-2)、(3-3)、(3-6)式进行信息素的全局更新;
Step 6:重复执行Step 2到Step 5,直到迭代次数iter_max达到指定的最大迭代次数或找到的解满足一定的精度为止;
Step 7:输出结果。
matlab源代码:
clear,clc;
[xdata,textdata]=xlsread('p_xy.xlsx'); %加载31个城市的数据
x_label=xdata(:,2); %第2列为横坐标
y_label=xdata(:,3); %第3列为纵坐标
C=[x_label y_label]; %坐标矩阵
n=size(C,1); %n表示城市个数
D=zeros(n,n); %D表示完全图的赋权邻接矩阵,即距离矩阵D初始化
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5; %计算两城市之间的距离
else
D(i,j)=0; %i=j, 则距离为0;
end
D(j,i)=D(i,j); %距离矩阵为对称矩阵
end
end
%%==================蚁群算法实现过程===========
%%============== 第一步 变量初始化==============
iter_max=100; % 最大迭代次数
m=30; % 蚂蚁个数
Alpha=1; % 表征信息素重要程度的参数
Beta=5; % 表征启发式因子重要程度的参数
Rho=0.8; % 信息素蒸发系数
Q=10; % 信息素增加强度系数
Eta=1./D; % Eta为能见度因数,这里设为距离的倒数
Tau=ones(n,n); % Tau为信息素矩阵,初始化全为1
Tabu=zeros(m,n); % 存储并记录路径的生成
nC=1; % 迭代计数器
R_best=zeros(iter_max,n); %各代最短路线,行为最大迭代次数,列为城市个数
L_best=inf.*ones(iter_max,1);%%各代最短路线的长度,inf为无穷大
L_ave=zeros(iter_max,1); % 各代平均路线长度
%%============== 第二步 将m只蚂蚁放到城市上===========
while nC<=iter_max %停止条件之一:达到最大迭代次数
Randpos=[];
for i=1:(ceil(m/n)) %ceil表示向无穷方向取整
Randpos=[Randpos,randperm(n)]; %randperm(n):表示随机产生一个整数排列
end
Tabu(:,1)=(Randpos(1,1:m))'; %每只蚂蚁(m只)都对应有一个位置,Tabu(:,1)为每只蚂蚁走过的第一个城市
%% ============== 第三步 m只蚂蚁按概率函数选择下一座城市,完成各自的周游==============
for j=2:n %城市从第二个开始
for i=1:m
visited=Tabu(i,1:(j-1)); %已访问的城市
J=zeros(1,(n-j+1)); %待访问的城市
P=J; %待访问城市的选择概率分布(初始化)
Jc=1; %循环下标
for k=1:n %利用循环求解待访问城市,如果第k个城市不属于已访问城市,则其为待访问城市
if length(find(visited==k))==0
J(Jc)=k;
Jc=Jc+1; %下表加1,便于下一步存储待访问的城市
end
end
for k=1:length(J) % 下面计算待访问城市的概率分布,length(J)表示待访问城市个数
P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta); %概率计算公式中的分子
end
P=P/(sum(P)); %概率分布:长度为待访问城市个数
Pcum=cumsum(P); %求累积概率和:cumsum([1 2 3])=1 3 6,目的在于使得Pcum的值总有大于rand的数
Select=find(Pcum>=rand); %按概率选取下一个城市:当累积概率和大于给定的随机数,则选择求和被加上的最后一个城市作为即将访问的城市
if isempty(Select) %若选择城市为空集,则随机将任一城市加入禁忌表中
Tabu(i,j)=round(1+(n-1)*rand);
else
next_visit=J(Select(1)); %next_visit表示即将访问的城市
Tabu(i,j)=next_visit; %将访问过的城市加入禁忌表中
end
end
end
if nC>=2;Tabu(1,:)=R_best(nC-1,:);end %若迭代次数大于等于2,则将上一次迭代的最佳路线存入到Tabu的第一行中
%% ==============第四步 记录本次迭代最佳路线==============
L=zeros(m,1);
for i=1:m;
R=Tabu(i,:);
for j=1:(n-1)
L(i)=L(i)+D(R(j),R(j+1)); %求路径距离
end
L(i)=L(i)+D(R(1),R(n)); %加上最后一个城市与第一个城市之间的距离
end
L_best(nC)=min(L); %最优路径为距离最短的路径
pos=find(L==L_best(nC)); %找出最优路径对应的位置:即为哪只蚂蚁
R_best(nC,:)=Tabu(pos(1),:); %确定最优路径对应的城市顺序
L_ave(nC)=mean(L); %求第k次迭代的平均距离
nC=nC+1;
%% ==============第五步 更新信息素,此处蚁周系统==============
Delta_Tau=zeros(n,n); %Delta_Tau(i,j)表示所有蚂蚁留在第i个城市到第j个城市路径上的信息素增量
for i=1:m
for j=1:(n-1) %建立了完整路径后在释放信息素
Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+Q/L(i);
end
Delta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+Q/L(i);
end
Tau=(1-Rho).*Tau+Delta_Tau; %信息素更新公式
%% ==============第六步 禁忌表清零==============
Tabu=zeros(m,n);
end
%% ==============第七步 输出结果==============
Pos=find(L_best==min(L_best)); %找到L_best中最小值所在的位置
Shortest_Route=R_best(Pos(1),:); %提取最短路径
Shortest_Length=L_best(Pos(1)); %提取最短路径长度
disp('最优解:')
p = OutputPath(Shortest_Route);
fprintf('总距离:%.3f\n',Shortest_Length);
fprintf('-------------------------------------------------------------\n');
%% ==============作图==============
figure; %作迭代收敛曲线图
x=linspace(0,iter_max,iter_max);
y=L_best(:,1);
plot(x,y,'-','LineWidth',2);
xlabel('迭代次数'); ylabel('最优值');
title('迭代过程');
%作最短路径图
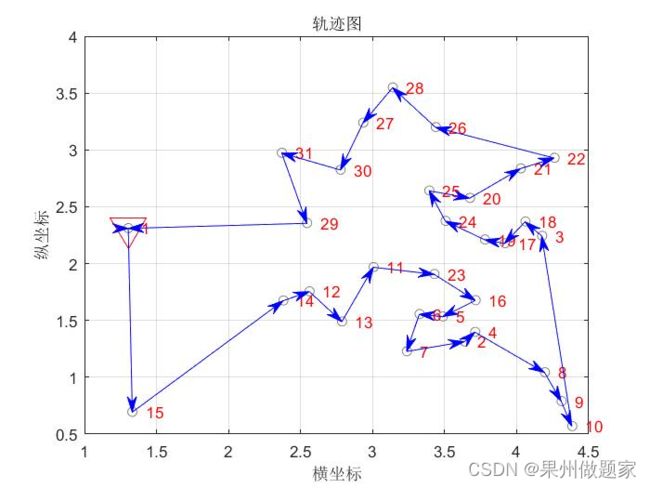
Shortest_Route=[Shortest_Route Shortest_Route(1)];
DrawPath(Shortest_Route, C);
五、结果分析
最优解:
1->15->14->12->13->11->23->16->5->6->7->2->4->8->9->10->3->18->17->19->24->25->20->21->22->26->28->27->30->31->29->1
总距离:15.609
完整源代码数据
链接:https://download.csdn.net/download/baidu/85291427