matlab遗传算法求解车辆路径问题(一)续
一、引言
上篇关于使用matlab编写遗传算法求解车辆路径问题写完后,我发现南柯一梦那篇文章的参考文献应该是一篇《中国管理科学》的文章《用混合遗传算法求解物流配送路径优化问题的研究》,果然期刊水平高,文章的质量还是更有保障。这篇文章提出用爬山算法对遗传算法进行改进,本文将对基于爬山算法的遗传算法进行复现,并用于求解原文中的车辆路径优化问题。问题描述在上一篇文章中,这里不再赘述。
二、算法思路及GA代码
2.0算法思路
本文针对VRP问题所编写代码的核心过程为车辆路径的分配过程,即把哪些顾客安排给第几辆车。不同于上一篇文章,本文代码中的种群个体没有包含虚拟配送中心,只包含了需要配送的需求点。所以首先要做的就是为顾客安排车辆,具体的思路如下。以6-9-4-2-1-3-8-7-5为例,首先将第一个顾客6安排给第一辆车(这里的隐含假设是,不存在需求量或配送距离大于单个车辆限额的顾客),接着计算将第二个顾客9加入第一个路径后的配送距离及载重量,如果都没超过,则将9安排给第一辆车,否则将9安排给下一个车辆,以此类推。
对于一个安排好车辆的个体,如果安排的车辆总数小于等于配送中心的车辆限额,则为可行解。如果安排的车辆总数大于配送中心得车辆限额,则对该个体进行惩罚。具体操作就是给该个体的总路径增加一个较大的惩罚值。接着进行的算法步骤为:选择-交叉-变异-爬山-重插入。爬山操作的思想是,对于通过遗传操作形成的每代群体中的最优个体,通过领域搜索实施爬山操作。具体做法是:(1)在个体中随机选择两个基因,交换其位置;(2)判断基因换位后适应值是否增加,若增加,则以换位后的个体取代原个体;(3)重复操作(1)(2)直到达到指定次数为止。
2.1车辆路径分配及个体总路径距离计算
%% LengthInd函数用于计算个体的总路径长度
% 输入:个体a,车辆数carNum,客户之间的距离里矩阵DL,
% 距离限制disMax,客户重量需求DW,车辆重量限制capMax,客户到需求点距离X
% 输出:个体的总路径长度
%%
% 整体思路是给个体中每个客户赋予对应的车辆编号,从小到大,
% 如果新增加的个体超过当前车辆的距离或重量限制,则分配给下一个车辆,
% 如果被分配的车辆总数超过了给定车辆数,对个体进行惩罚
function lengthInd = LengthInd(a,carNum,DL,disMax,DW,capMax,X)
custNum = length(a); % 记录顾客的数量
matchA = zeros(custNum,4); % 记录顾客和车辆的匹配情况,第一列为顾客的编号,第二列为匹配的车辆编号
% 第三列为子路径总距离只记录在一个路径最后一个顾客对应的位置,第四列为需求重量
matchA(:,1) = a';
matchA(:,4) = DW(a)';
matchA(1,2) = 1; % 第一个顾客一定在第一个路径中
k = 1; % 车辆的编号
for i = 2:custNum
% 对于第i个顾客,首先要计算的是在当前路径加入该顾客后的路径总距离以及总重量
custTemp = find(matchA(:,2)==k); % 先找到第k个路径中包含的顾客
custK = [matchA(custTemp,1)' matchA(i,1)]; % 在第k个路径中加入第i个顾客后的总顾客情况
i1 = custK(1:end-1);
i2 = custK(2:end);
custKL = sum(DL((i1-1)*custNum+i2));
custKL = custKL + X(custK(1)) + X(custK(end)); % 计算第k辆车的总路径
custKW = sum(DW(custK)); % 计算第k辆车的总载重
if (custKL > disMax || custKW > capMax)
k = k + 1;
matchA(i,2) = k;
% 此时判断出了上一辆车的最后一个需求点,因此需要记录上一个路径的距离
custK(end) = [];
i1 = custK(1:end-1);
i2 = custK(2:end);
custKL = sum(DL((i1-1)*custNum+i2));
custKL = custKL + X(custK(1)) + X(custK(end));
matchA(i-1,3) = custKL;
else
matchA(i,2) = k;
end
if i == custNum
i1 = custK(1:end-1);
i2 = custK(2:end);
custKL = sum(DL((i1-1)*custNum+i2));
custKL = custKL + X(custK(1)) + X(custK(end));
matchA(i-1,3) = custKL;
end
end
aLength = sum(matchA(:,3)); % 计算a的总路径
if matchA(end,2) > carNum
lengthInd = aLength + 1000; % 车辆数超过限制,给予惩罚
else
lengthInd = aLength;
end2.2选择
本文中选择操作采用的是轮盘赌方式,具体代码如下:
%% Select函数采用轮盘赌方式对种群中的个体进行选择
% 输入:种群population,车辆数carNum,客户之间的距离里矩阵DL,
% 距离限制disMax,客户重量需求DW,车辆重量限制capMax,客户到需求点的距离X
% 输出:选择后的种群newPop
%%
function newPop = Select(population,carNum,DL,disMax,DW,capMax,X)
% 首先对种群的适应度进行计算
popNum = size(population,1); % 记录种群的个数
fitInd = zeros(popNum,1); % 记录个体的适应度
newPop = population; % 记录选择后的个体
for i = 1:popNum
fitInd(i) = 1/LengthInd(population(i,:),carNum,DL,disMax,DW,capMax,X);
end
probInd = fitInd./sum(fitInd); % 每个个体被选择的概率
probIndAcu = cumsum(probInd); % probIndAcu是probInd的累加概率,这一步为轮盘构建
for i = 1:popNum
newPop(i) = population(popNum - length(find(rand<=probIndAcu)) + 1); % 根据轮盘赌概率选择个体
end2.3交叉
首先是配对函数
function [new_pop_intercross]=Mating_pool(population_num,population,Pc)
%%
%输入:population,population_num,Pc
%输出:1.new_popopulation_intercross
% 2.c3,配对池:随机将种群population两两配对
% 3.pool
%%
pl=randperm(population_num); % 将种群打散用于配对
num=population_num/2;
c3=zeros(2,num);
pool=[];
new_pop_intercross=population;
for kj=1:num
c3(1,kj)=pl(2*kj-1);
c3(2,kj)=pl(2*kj);
end %生成"配对池c3
%%判断“配对池c3”每一对个体的随机数是否小于交叉概率Pc
rd=rand(1,num);
for kj=1:num
if rd(kj)其次是两个体的交叉函数
% 因为VRP问题中的一个重要约束是要遍历需求点,且每个点只访问一次,所以A,B两个染色体配对成功后
% 首先要确定交叉的基因段,选择好后先对染色体A进行交叉操作,清楚A中交叉基因段,在B中找到A中被
% 清除的需求点的位置,去除B中其余的需求点,将剩余的需求点直接插入A中的交叉基因段,这样就保证了
% 染色体A仍然遍历所有的需求点且每个需求点只经过一次
function [A,B]=cross(A,B)
A_1=A;
B_1=B;
r=randperm(length(A));
c=min(r(1,1:2));
d=max(r(1,1:2));
for i=c:d
A(i)=0;
end
B_1(ismember(B_1,A))=[];
A(1,c:d)=B_1;
for i=c:d
B(i)=0;
end
A_1(ismember(A_1,B))=[];
B(1,c:d)=A_1;
end2.4变异
function [Mut_Pop]=Mutation(Cross_Pop,Pm)
Mut_Pop=Cross_Pop;
Cross_Pop_num=size(Cross_Pop,1);
for j=1:Cross_Pop_num
A=Cross_Pop(j,:); % 要进行变异的染色体
A_1=A; % 对A进行记录,之后交换变异需求点的时候要用到
n=size(A,2);
r=rand(1,n);
Pe=find(r2.5爬山
%% ClimbMoun函数对变异后的最优个体进行爬山寻优操作
% 输入:个体a,车辆数carNum,客户之间的距离里矩阵DL,
% 距离限制disMax,客户重量需求DW,车辆重量限制capMax,客户到需求点距离X
% 输出:爬山寻优后的个体
function aClimb = ClimbMoun(a,carNum,DL,disMax,DW,capMax,X)
aNum = length(a); % 记录a的长度
lengthOrigina = LengthInd(a,carNum,DL,disMax,DW,capMax,X);
for i = 1:100 % 爬山寻优次数
temp = a;
r1 = randsrc(1,1,1:aNum);
r2 = randsrc(1,1,1:aNum); % 在1-aNum中找出两个随机数
while r1 ==r2
r2 = randsrc(1,1,1:aNum);
end
tempr1 = temp(r1);
temp(r1) = temp(r2);
temp(r2) = tempr1;
lengthClimba = LengthInd(temp,carNum,DL,disMax,DW,capMax,X);
if lengthOrigina > lengthClimba % 寻得更优个体
aClimb = temp;
break;
end
end
if lengthOrigina <= lengthClimba % 未寻得更优个体
aClimb = a;
end2.6主函数
clc
clear
close all;
tic;
%% 算法参数
popNum=80; % 种群规模
Max_gen=300; % 迭代次数
Pc=0.8; % 交叉概率
Pm=0.05; % 变异概率
%% 问题参数
carNum=5; % 车辆最大数量
custNum=20; % 顾客人数
capMax=8; % 每辆车的载重限制
disMax=50; % 每辆车的总路径限制
trace = zeros(2,Max_gen); % 用于记录总路径的进化过程
load data_DW % 加载需求点的位置和需求量数据
%%
% 种群初始化,并计算需求点之间的距离矩阵DL,需求量DW,配送中心到需求点距离X
DL = zeros(custNum,custNum); % 建立需求点之间的距离矩阵
X = zeros(1,custNum); % 建立需求点到配送中心的距离
for i = 1:custNum
for j = i:custNum
DL(i,j) = ((data_DW(i,1)-data_DW(j,1))^2+(data_DW(i,2)-data_DW(j,2))^2)^0.5;
DL(j,i) = DL(i,j);
end
X(i) = ((data_DW(i,1)-data_DW(custNum + 1,1))^2+(data_DW(i,2)-data_DW(custNum + 1,2))^2)^0.5;
end
DW = data_DW(:,3)'; % 建立需求点的重量
population=zeros(popNum,custNum);
for i=1:popNum
population(i,:)=randperm(custNum); % 产生含有虚拟配送中心的随机个体
end
%% 基于爬山算法的遗传算法
y=1;%循环计数器
Total_Dis = zeros(popNum,1);
for i = 1:popNum
Total_Dis(i) = LengthInd(population(i,:),carNum,DL,disMax,DW,capMax,X);
end
trace(2,1) = min(Total_Dis);
while y2.7得出车辆分配结果
这个函数和路径计算函数差不多,但我对函数的运用还不太熟练,所以又增加了一个函数对其进行求解
%% CarAllocate函数用于得到个体的车辆安排
% 输入:个体a,车辆数carNum,客户之间的距离里矩阵DL,
% 距离限制disMax,客户重量需求DW,车辆重量限制capMax,客户到需求点距离X
% 输出:个体的车辆安排
%%
% 整体思路是给个体中每个客户赋予对应的车辆编号,从小到大,
% 如果新增加的个体超过当前车辆的距离或重量限制,则分配给下一个车辆,
% 如果被分配的车辆总数超过了给定车辆数,对个体进行惩罚
function carAllocate = CarAllocate(a,DL,disMax,DW,capMax,X)
custNum = length(a); % 记录顾客的数量
matchA = zeros(custNum,4); % 记录顾客和车辆的匹配情况,第一列为顾客的编号,第二列为匹配的车辆编号
% 第三列为子路径总距离只记录在一个路径最后一个顾客对应的位置,第四列为需求重量
matchA(:,1) = a';
matchA(:,4) = DW(a)';
matchA(1,2) = 1; % 第一个顾客一定在第一个路径中
k = 1; % 车辆的编号
for i = 2:custNum
% 对于第i个顾客,首先要计算的是在当前路径加入该顾客后的路径总距离以及总重量
custTemp = find(matchA(:,2)==k); % 先找到第k个路径中包含的顾客
custK = [matchA(custTemp,1)' matchA(i,1)]; % 在第k个路径中加入第i个顾客后的总顾客情况
i1 = custK(1:end-1);
i2 = custK(2:end);
custKL = sum(DL((i1-1)*custNum+i2));
custKL = custKL + X(custK(1)) + X(custK(end)); % 计算第k辆车的总路径
custKW = sum(DW(custK)); % 计算第k辆车的总载重
if (custKL > disMax || custKW > capMax)
k = k + 1;
matchA(i,2) = k;
% 此时判断出了上一辆车的最后一个需求点,因此需要记录上一个路径的距离
custK(end) = [];
i1 = custK(1:end-1);
i2 = custK(2:end);
custKL = sum(DL((i1-1)*custNum+i2));
custKL = custKL + X(custK(1)) + X(custK(end));
matchA(i-1,3) = custKL;
else
matchA(i,2) = k;
end
end
carAllocate = matchA(:,2)';
三、算例展示
这里的算例选用的是文章中的实例2,首先将需要载入的数据给出,及配送中心和需求点的坐标及需求量
12.8000000000000 8.50000000000000 0.100000000000000
18.4000000000000 3.40000000000000 0.400000000000000
15.4000000000000 16.6000000000000 1.20000000000000
18.9000000000000 15.2000000000000 1.50000000000000
15.5000000000000 11.6000000000000 0.800000000000000
3.90000000000000 10.6000000000000 1.30000000000000
10.6000000000000 7.60000000000000 1.70000000000000
8.60000000000000 8.40000000000000 0.600000000000000
12.5000000000000 2.10000000000000 1.20000000000000
13.8000000000000 5.20000000000000 0.400000000000000
6.70000000000000 16.9000000000000 0.900000000000000
14.8000000000000 2.60000000000000 1.30000000000000
1.80000000000000 8.70000000000000 1.30000000000000
17.1000000000000 11 1.90000000000000
7.40000000000000 1 1.70000000000000
0.200000000000000 2.80000000000000 1.10000000000000
11.9000000000000 19.8000000000000 1.50000000000000
13.2000000000000 15.1000000000000 1.60000000000000
6.40000000000000 5.60000000000000 1.70000000000000
9.60000000000000 14.8000000000000 1.50000000000000
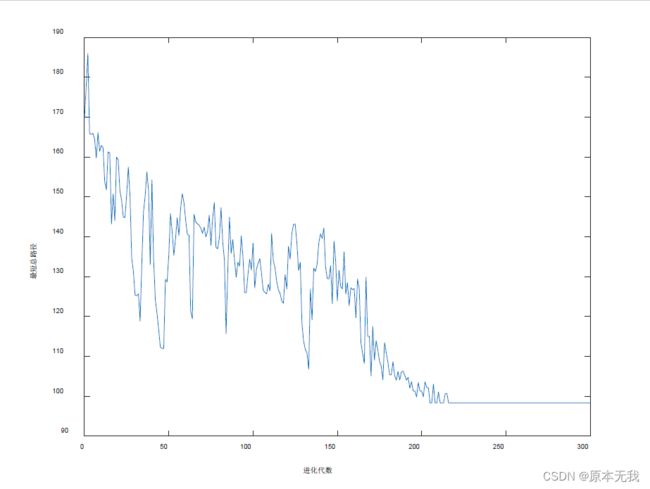
14.5000000000000 13 0多次实验得到的最优解为98.3Km,具体的路径安排如下, 0-14-4-3-17-18-0, 0-20-11-6-13-19-8-0, 0-7-15-9-12-2-10-1-5, 0-4-0,进化情况如图所示。10次实验所得到的平均最短路径长度为109.27Km,结果均由于原文的结果。
参考文献
[1] 郎茂祥,胡思继.用混合遗传算法求解物流配送路径优化问题的研究[J].中国管理科学,2002(05):52-57.DOI:10.16381/j.cnki.issn1003-207x.2002.05.011.
[2] 遗传算法求解车辆路径问题 - 知乎