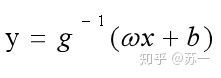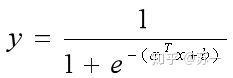机器学习笔记（二）：线性模型

线性模型是机器学习常用的众多模型中最简单的模型，但却蕴含着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射得到，因此了解线性模型对学习其他机器学习模型具有重要意义。
本文主要介绍机器学习中常用的线性模型，内容主要包括：

一、 线性回归（Linear Regression）

二、 对数几率回归（Logistic Regression）

三、 线性判别分析(Linear Discriminant Analysis)

四、 多分类学习(Multi class learning）

一、 线性回归（Linear Regression）

给定数据集D={（x1,y1）,(x2,y2),(x3,y3),……,(xn,yn)},其中xi为第i组数据的属性集合，yi为第i组数据的标记。线性回归试图学得一个从xi映射到yi的线性模型(ω,b)，即

当给定一个新的输入属性xj时，该模型能尽可能准确地预测实值输出标记yj。

在通常情况下我们很难得到一个完美的模型来对于所有的输入都给出正确的输出，大多数场景我们训练出的模型只能对一部分输入给出正确答案，因此我们需要设置一个评价指标，来衡量训练出的模型的性能。在回归任务中最常用的度量性能方法是“均方误差”

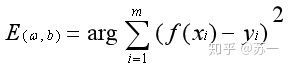
几何意义上是求得一条线，使得所有的样本到直线的欧式距离之和最小。基于均方误差最小化标准进行模型求解的方法称为最小二乘“参数估计”。其具体过程为，首先均方误差函数对ω和b求偏导：

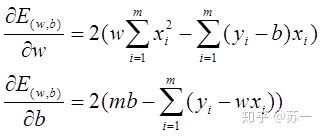
然后，令以上两式为0即可获得ω和b的解。

以上便是求解线性回归模型的过程，它的前提假设是预测值yi与输入xi之间存在着线性关系，但有时在我们处理的问题中可能是预测值的对数与输入值存在线性关系，或者预测值与输入值存在着更为复杂的函数关系，为了解决这种情况，于是便产生了对数线性回归（log-linear regression）和广义线性回归（generalized linear regression）的概念，他们的模型分别如下：

其中函数g(…)称为“联系函数”

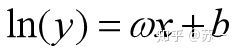
二、 对数几率回归（Logistic Regression）

线性回归模型产生的预测值是实值，对于分类任务比如需要判断明天是天晴还是下雨就不适用了。对数几率回归的提出正是用来解决分类任务的，它在线性模型的基础上将预测值yi转化为接近于指定的有限个值的输出。最常用的转化方法是通过sigmoid函数，转化为o或1两个值，适用于二分类任务。

对数几率回归虽然名字是回归，但实际是一种分类学习方法。

三、 线性判别分析(Linear Discriminant Analysis)

线性判别分析（linear Discriminant Analysis,简称LDA）是一种经典的线性学习方法，他的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。下图是一个二维的二分类示意图，相同颜色的点在直线上的投影距离很近，不同颜色的点距离较远。

此方法步骤较为复杂，具体操作，大家可参考这篇博文中的内容https://blog.csdn.net/daunxx/article/details/51881956

四、 多分类学习(Multi class learning）

在前面介绍的两个方法中所使用的例子都是二分类任务，但在现实生活中我们遇见的多分类任务更多一些。由于二分类任务的解决方法较为简单，因此在很多情形下，我们可以基于一些策略，利用二分类学习器来解决多分类问题。最经典的拆分策略有三种，分别是：“一对一（One VS One,OvO）”、“一对其余(One vs Rest,OvR)”和“多对多(Many vs Many,MvM”.

1、一对一：给定数据集D假定其中有N个真实类别，从使用分而治之的思路，将这N个类别进行两两配对(一个正类/一个反类)，从而产生N(N-1)/2个二分类学习器，每个学习器对一种类别进行判别。在测试阶段，将新样本放入所有的二分类学习器中测试，得出N(N-1)个结果，最终通过投票产生最终的分类结果。训练N个分类器，开销较大。

2、一对其余：给定数据集D假定其中有N个真实类别，每次取出一个类作为正类，剩余的所有类别作为一个新的反类，从而产生N个二分类学习器，在测试阶段得出N个结果若仅有一个学习器预测为正类，则对应的类标作为最终分类结果。优时也要考虑预置置信度的大小确定类别。

3、多对多：给定数据集D假定其中有N个真实类别，每次取若干个类作为正类，若干个类作为反类（通过ECOC码给出编码），若进行了M次划分，则生成了M个二分类学习器，在测试阶段（解码），得出M个结果组成一个新的码，最终通过计算海明/欧式距离选择距离最小的类别作为最终分类结果。

参考资料

1、周志华，《机器学习》

2、Duanxx，线性判别分析（Linear Discriminant Analysis），https://blog.csdn.net/daunxx/article/details/51881956