数字图像处理Matlab-图像压缩与离散余弦变换(附代码)
目录
-
- 1.Objectives:
- 2.Experiment Content:
- 3.Experiment Principle:
- 4.Experiment Steps Result and Conlusion:
-
- 1、操作使用 mat2lpc, lpc2mat, entropy, imratio, compare 等函数,了解其作用和特点。
- 2、Huffman 编码
- 3、编写无损预测编解码(lossless predictive coding)程序,使 p313Figure 8.7图具有更低的熵(5.4436) 。
- 4、DCT 离散余变换
- 3 DCT处理后的结果
- 【附录】实现代码
1.Objectives:
1、理解有损压缩和无损压缩的概念;
2、理解图像压缩的主要原则和目的;
3、利用 MATLAB 程序进行图像压缩。
4、学习 DCT 离散余变换的特性及实现方法。
2.Experiment Content:
1、利用 matlab 程序实现图像压缩,学会 mat2huff, huff2mat,mat2lpc, lpc2mat, im2jpeg, jpeg2im, entropy, imratio, compare使用方法。
2、编程实现分块图像 DCT 离散余变换,并实现频域滤波
3.Experiment Principle:
见书《数字图像处理》
(冈萨雷斯著作,电子工业出版社于2009年12月1日出版)
4.Experiment Steps Result and Conlusion:
1、操作使用 mat2lpc, lpc2mat, entropy, imratio, compare 等函数,了解其作用和特点。

 Conv:使用mat2lpc对原图进行去除空间冗余的编码,使用lpc2mat对图像进行解码。分别使用entropy和nrtop函数对编码前后图像计算熵,均可看到熵的减少。最后再用imratio计算压缩比,用compare计算误差发现为0,即完美传输图像。
Conv:使用mat2lpc对原图进行去除空间冗余的编码,使用lpc2mat对图像进行解码。分别使用entropy和nrtop函数对编码前后图像计算熵,均可看到熵的减少。最后再用imratio计算压缩比,用compare计算误差发现为0,即完美传输图像。
注:
Out= entropy(Img) 其物理意义:如果一幅图(或一组数字中)有n种不同的取值,每种取值站的比率为p(i), i=1,…,n
那么这个函数求的熵就是 -sum(p(i).*log2[p(i)]),通俗来讲就是对每个p求其对应的p(i).*log2[p(i)],然后再把这些所有结果加起来再取相反数。
一个例程:
Img=imread(‘1.jpg’);
%把文件命为’1.jpg’的图片读取为变量Img
%这里注意Img要是灰度图,只能有一个颜色通道
Out= entropy(Img) %这一句就计算出了整幅图的熵。图像处理中经常见到把图像分成一块一块的,然后对每一块求熵,这样得到的是一个熵的分布图。
Nrtop函数:求熵,表示信源的平均信息量。也表示原灰度图像对应编码后的样本的不同概率,若熵越小则对应不同样本的概率差别越大,则越能分出正确的样本,说明编码越有效。
2、Huffman 编码
使用 mat2huff,huff2mat 实现 Huffman 编解码,并应用 imratio计算编码后信号的压缩率。

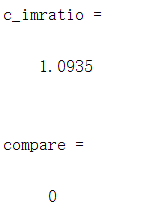
Conv:经过霍夫曼编码和解码后发现,误差为0,完美传输。
3、编写无损预测编解码(lossless predictive coding)程序,使 p313Figure 8.7图具有更低的熵(5.4436) 。
显示预测误差(predictionerror)图。
用解码程序解码,并验证解码是否正确(compare) 。

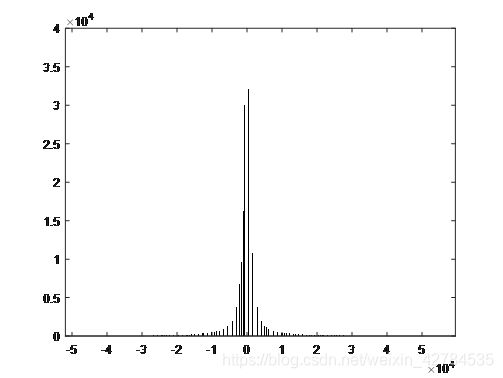
 Conv:将解码后图像和原图进行比较,可得误差为0,可知为无损传输。观察预测误差的直方图可知,0周围的峰值很高,预测和微分去除了大部分的空间冗余。
Conv:将解码后图像和原图进行比较,可得误差为0,可知为无损传输。观察预测误差的直方图可知,0周围的峰值很高,预测和微分去除了大部分的空间冗余。
4、DCT 离散余变换
1)将输入图像分解为8×8 的块。
2)对每个块进行二维DCT 变换。
3)将图像变换到频域。
4)每个块只保留部分DCT的系数(可分别保留1,5,10,30 和64 个系数)。
5)进行 DCT 反变换的滤波图像。
1,图像在频域的显示

从上图看出,图像横向频带窄,说明变化比较慢,纵向频带宽,说明包含一些较高频的分量,变化比较快。从原图来看,确实满足这一点
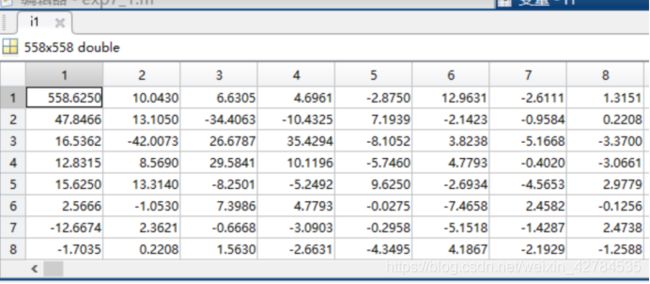
2,系数展示
这是保留一个系数的数据
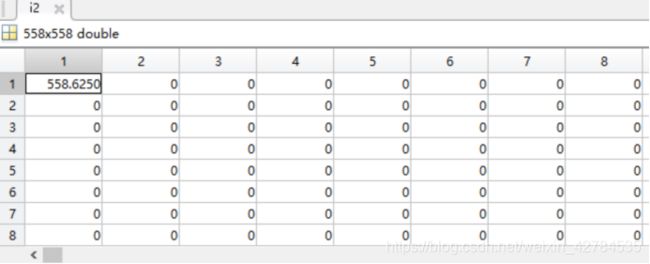
这是保留5个系数的数据
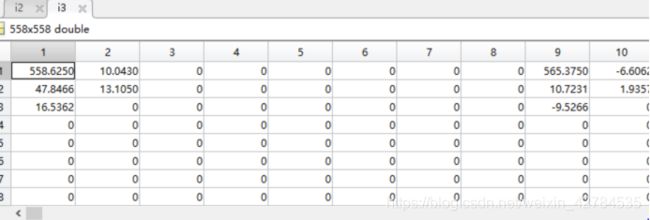
后面的数据出现是分块处理的结果,可以看出每块都进行了相同的操作,保留了相同数量的系数
这是保留10个系数的数据
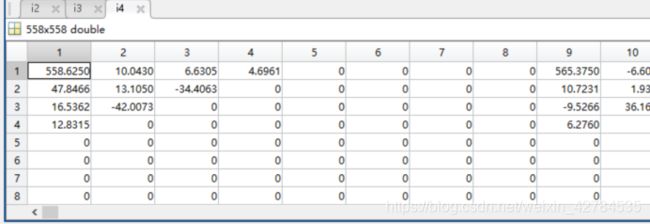
这是保留30个系数的数据
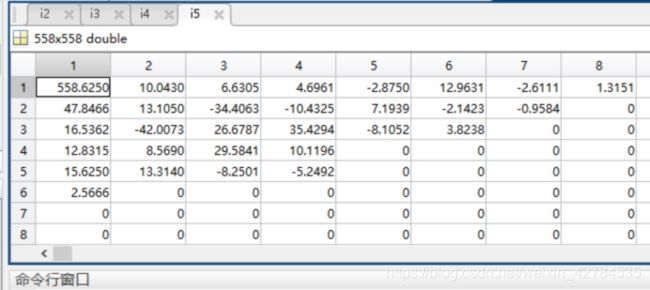
保留这些数据得到的结果如下:

Conv:从图中可以看到,五张复原后的图片从大体上看,没有什么太大的区别,当然由于取得的系数不一样还是有一些区别的,但是很小,说明这种要压缩会取得很高的压缩比。从系数的数据来看,这种现象也不难理解,变换后的第一个数据值为558 后面的数据就是10 40 相比较来说很小了,因此其主要信息就是集中在第一块数据中的
注:
DCT变换的全称是离散余弦变换(Discrete Cosine Transform),主要用于将数据或图像的压缩,能够将空域的信号转换到频域上,具有良好的去相关性的性能。DCT变换本身是无损的,但是在图像编码等领域给接下来的量化、哈弗曼编码等创造了很好的条件,同时,由于DCT变换时对称的,所以,我们可以在量化编码后利用DCT反变换,在接收端恢复原始的图像信息。
DCT变换在当前的图像分析已经压缩领域有着极为广大的用途,我们常见的JPEG静态图像编码以及MJPEG、MPEG动态编码等标准中都使用了DCT变换。
在实际的图像处理中,DCT变换的复杂度其实是比较高的,所以通常的做法是,将图像进行分块,然后在每一块中对图像进行DCT变换和反变换,再合并分块,从而提升变换的效率。具体的分块过程中,随着子块的变大,算法复杂度急速上升,但是采用较大的分块会明显减少图像分块效应,所以,这里面需要做一个折中,在通常使用时,大都采用的是8*8的分块。
3 DCT处理后的结果

Conv:主要看第二个图,可以看到图片的经过变换后的主要能量集中在左上角,这也就不难理解为啥系数要按照Zigzag的方式进行排列了
原图与反变换后数据分析:
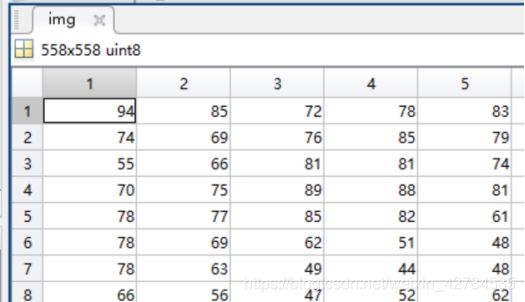
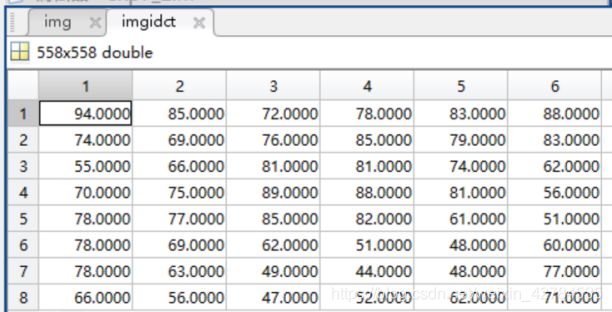 可以看到除了数据类型外,数据值基本一致
可以看到除了数据类型外,数据值基本一致
【附录】实现代码
程序一
clear all;clc;
addpath('E:\数字图像处理\程序与图像\dipum_toolbox_2.0.2(only run)');%添加相应的.p文件
f=imread('columbia.tif');
figure(1);
subplot(131);imshow(f);title('原图');
e=mat2lpc(f);
subplot(132);imshow(mat2gray(e));title('去除空间冗余后图像');
f_ntrop=ntrop(f)%计算原图和编码后的熵
e_ntrop=ntrop(e)
f_entropy=entropy(f)%计算原图和编码后的熵
e_entropy=entropy(e)
e_imratio=imratio(f,e)%计算编码后的压缩比 g=lpc2mat(e);%解码
subplot(133);imshow(g,[]);title('解码后图像');
compare=compare(f,g)%比较两幅图像的误差
程序二
clear all;clc;
addpath('E:\数字图像处理\程序与图像\dipum_toolbox_2.0.2(only run)');%添加相应的.p文件
f=imread('columbia.tif');
figure(1);
subplot(121);imshow(f,[]);title('原图');
c=mat2huff(f);
c_imratio=imratio(f,c)
g=huff2mat(c);
subplot(122);imshow(g,[]);title('解码后图像');
compare=compare(f,g)%比较两幅图像的误差
程序三
clear all;clc;
addpath('E:\数字图像处理\程序与图像\dipum_toolbox_2.0.2(only run)');%添加相应的.p文件
f=imread('columbia.tif');
e=mat2lpc(f);%求出预测误差图像,这里其实也是获得纵向边沿的一种方式%就是把图像向右移动一个数,然后再减去原图像
figure(1);
subplot(131);imshow(f,[]);title('原图');
subplot(132);imshow(mat2gray(e));title('lpc预测误差图像');
f_entro=entropy(f)
g_entro=entropy(e)
%压缩编码
c=mat2huff(e);
cr=imratio(f,c)
g=lpc2mat(huff2mat(c));
subplot(133);imshow(g,[]);title('压缩并解压后的图像');
compare=compare(f,g)
[h,x]=hist(e(:)*512,512);
figure(2);
bar(x,h,'k');
程序四
img=imread('Fig0907(c).tif');
i1=blkproc(img,[8 8],@dct_sdu);
%此函数的主要作用是将输入的图像或者说是矩阵分快处理%第一个参数就是输入要进行处理的数据 第二个参数代表着要进行分块处理的矩阵的大小即行列,
%第三个是一个函数句柄,代表着要如何处理这个矩阵fs=fftshift(fft(img));
%这是将图像从空间域转换到频域上,然后再把低频放到图像中间位置
figure,imshow(abs(fs),[]);%显示频域图形
title('图像变换到频域');
%这是为了提取特定个数的系数来制造的mask,分别对应着取1,5,10,30 和64 个系数的时候,
%因为dct的系数是按照Zigzag的形式排列的(横斜竖斜...),我们通过制造mask与对应的系数矩阵相乘,%留下来系数的地方mask中对应的值为1,剩下的为0,即可以通过相乘的方式取得我们想要的系数
mask1=[1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%取1个系数的时候对应的mask
mask2=[1 1 0 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%取5个系数的时候对应的mask
mask3=[1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%取10个系数的时候对应的mask
mask4=[1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 0
1 1 1 1 0 0 0 0
1 1 1 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%取30个系数的时候对应的mask
%将通过dct变换留下来的系数与mask相乘,其中P1代表句柄的输入值mask,x代表分快处理中的每一块
i2=blkproc(i1,[8 8],'P1.*x',mask1);
i3=blkproc(i1,[8 8],'P1.*x',mask2);
i4=blkproc(i1,[8 8],'P1.*x',mask3);
i5=blkproc(i1,[8 8],'P1.*x',mask4);
%再分块进行反变换操作
ii1=blkproc(i1,[8 8],@idct_sdu);
ii2=blkproc(i2,[8 8],@idct_sdu);
ii3=blkproc(i3,[8 8],@idct_sdu);
ii4=blkproc(i4,[8 8],@idct_sdu);
ii5=blkproc(i5,[8 8],@idct_sdu);
figure%显示结果
subplot(2,3,1),imshow(img),title('原图像');
subplot(2,3,2),imshow(ii2,[]),title('取1个dct系数');
subplot(2,3,3),imshow(ii3,[]),title('取5个dct系数');
subplot(2,3,4),imshow(ii4,[]),title('取10个dct系数');
subplot(2,3,5),imshow(ii5,[]),title('取30个dct系数');
subplot(2,3,6),imshow(ii1,[]),title('取64个dct系数');
img = imread('cameraman.tif');
imgdct = dct_sdu(img); %不进行分快处理,直接进行DCT 正向变换
imgidct = idct_sdu(imgdct); %DCT 逆变换
figure (1);
subplot(131);
imshow(img); title('原始图象')
subplot(132);
%imshow(imgdct,[]);
imshow(uint8(imgdct));%因为imgdct的值范围很大,值特别大的数很少,直接显示视觉上一片黑色
%因此用uint8,把255以上的都用白点,0以下的用黑点,这样能看清楚主要能量集中在哪儿
title('DCT 变换图象(不分块)');
subplot(133);
%imshow(imgidct,[]);imshow(uint8(imgidct));%显示,因为是double型的先变成uint8,再显示
title('DCT 逆变换图象');
子程序dct_sdu:
function Y=dct_sdu(X) %子程序定义
[m,n] = size(X); %得到输入图像的大小m*n
AM = zeros(m,m); %得到m*m的零矩阵
AN = zeros(n,n); %得到n*n的零矩阵
for i = 0:m-1 %根据DCT算法得到AM矩阵中每一元素的值
for j = 0:m-1
if i == 0
AM(i+1,j+1) = sqrt(1/m)*cos(((2*j+1)*i*pi)/(2*m));
else AM(i+1,j+1) = sqrt(2/m)*cos(((2*j+1)*i*pi)/(2*m));
end
end
end
for i = 0:n-1 %根据DCT算法得到AN矩阵中每一元素的值
for j = 0:n-1
if i == 0
AN(i+1,j+1) = sqrt(1/n)*cos(((2*j+1)*i*pi)/(2*n));
else AN(i+1,j+1) = sqrt(2/n)*cos(((2*j+1)*i*pi)/(2*n));
end
end
end
X = double(X); %将X转化为double形式
Y = AM*X*AN';
%将AN矩阵和输入图像的矩阵和AN的逆矩阵相乘,得到DCT变换后结果
end
子程序idct_sdu:
function Y=idct_sdu(X) %同上
[m,n] = size(X);
AM = zeros(m,m);
AN = zeros(n,n);
for i = 0:m-1
for j = 0:m-1
if i == 0
AM(i+1,j+1) = sqrt(1/m)*cos(((2*j+1)*i*pi)/(2*m));
else AM(i+1,j+1) = sqrt(2/m)*cos(((2*j+1)*i*pi)/(2*m));
end
end
end
for i = 0:n-1
for j = 0:n-1
if i == 0
AN(i+1,j+1) = sqrt(1/n)*cos(((2*j+1)*i*pi)/(2*n));
else AN(i+1,j+1) = sqrt(2/n)*cos(((2*j+1)*i*pi)/(2*n));
end
end
end
X = double(X);
Y = AM'*X*AN;
%将AM矩阵的逆矩阵和输入图像的矩阵和AN矩阵相乘,得到IDCT反变换后结果
end
码字不易,都看到这里了不如点个赞哦~
我还写了很多文章,欢迎关注我哦~
![]()
亲爱的朋友,这里是我的公众号,欢迎关注!
本博客的优秀博文也将陆续搬运到公众号,之后还将推出更多优秀博文,并将优先发在公众号,敬请期待!
关注起来,让我们一起成长!
![]()