SMD-Net_首次在立体匹配任务中使用连续变量表示(CVPR 2021)
文章目录
- 概述
- 模型
-
- 问题定义
- SMD-Nets
-
- backbone
- SMD-Head
- 损失函数
- 采样策略
- 实验
-
- 数据集
- 消融实验
-
- 不同的输出表达形式:视差回归、单峰拉普拉斯分布与双峰分布
- 不同采样策略
- 不同视差真值分辨率
- 与当前Baseline的比较
- 结论
- 参考文献
概述
论文名称: SMD-Nets: Stereo Mixture Density Networks
论文链接: https://openaccess.thecvf.com/content/CVPR2021/papers/Tosi_SMD-Nets_Stereo_Mixture_Density_Networks_CVPR_2021_paper.pdf
开源代码链接: https://github.com/fabiotosi92/SMD-Nets
作者单位: University of Bologna、 MPI-IS / University of Tubingen
被引: 4
SMD-Nets是2021年的CVPR,是第一篇在立体匹配任务中使用连续函数表达的文章。
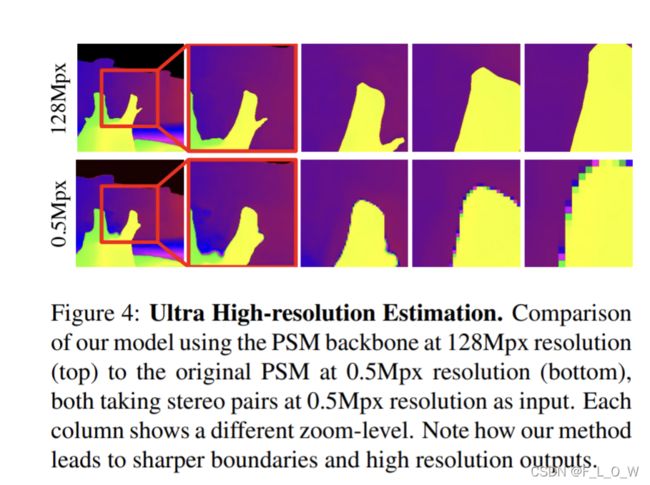
这篇文章主要希望解决两个问题,一个是解决边缘处像素的过平滑问题,再一个是解决超分/上采样效果不好的问题。
对于过平滑问题,其思想是边缘处的像素理应要么是前景要么是背景,所以其网络输出为双峰分布,在推理时,哪个峰的概率更高就选择其对应的那个像素。
而对于第二个问题,不同于传统双线性采样只考虑说待填充视差值附近的视差值,进而进行插值,而是说对于待填充视差值的坐标来说,先通过插值的方式找到对应的原图特征,进而通过特征对视差进行预测。
贡献:
- 一种新颖的立体匹配学习框架,利用紧凑的参数化双峰混合密度作为输出表示,并可以使用简单的基于似然的损失函数进行训练。其简单的公式提升了深度不连续处的锐利表现,并提供了不确定性度。
- 一个连续函数公式的表达,旨在不增大内存占用的前提下,得到任意空间分辨率的视差图。
- 一种高分辨率、大规模合成的双目立体数据集,其视差真值分辨率为3840x2160,场景包括室内和室外。
模型
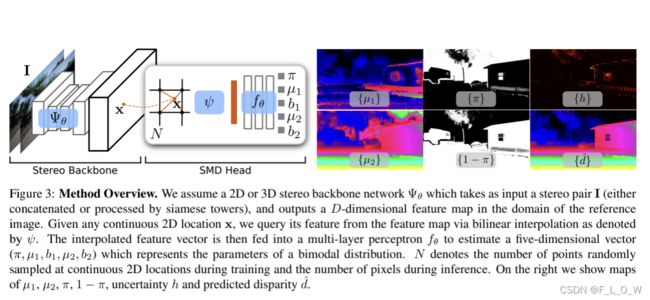
首先使用卷积backbone将输入的立体图像编码为特征图,而后通过MLP来估计任意2D位置的混合密度概率分布参数,对于多层感知机来说,其输入为经由双线性插值的特征向量。由此,可以获得一个视差图和一个不确定度图。图片中的 π \pi π为选择背景视差的概率。
问题定义
不妨设一对RGB的立体图像为 I ∈ R W ∗ H ∗ 6 \mathbf{I} \in \mathbb{R}^{W * H * 6} I∈RW∗H∗6,任意分辨率的视差图为 D \mathbf{D} D。对于经典的视差回归网络来说,总是会有着over-smoothing的问题,这是因为网络更趋向于学习平滑的低频信息。示意图见下:
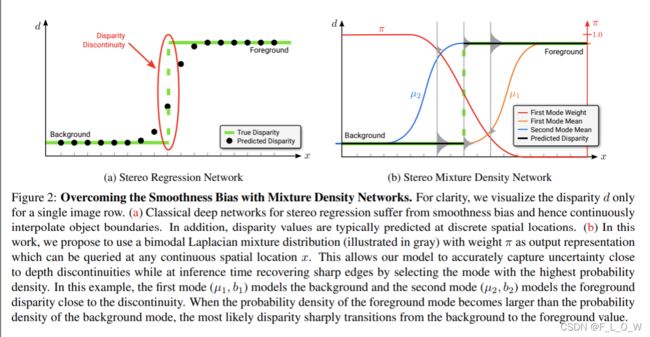
在SMD的工作中,针对该问题,探索了以一个混合分布作为输出的解决方案。
具体地,提出了一个双峰拉普拉斯混合分布,使用权重 π \pi π,以及两对mode参数 ( μ 1 , b 1 ) (\mu_1,b_1) (μ1,b1), ( μ 2 , b 2 ) (\mu_2,b_2) (μ2,b2),来对某一个特定像素上的视差连续概率分布进行建模。使用两对参数的好处是,使得网络能够同时捕捉边缘处的前景和背景的视差。
在推理时,则选择最优的那一对参数,而所谓的最优则是指有着“the highest density value”。
因此,我们的模型可以在不连续的区域直接从一个视差变为另一个视差,而实现这样的过程只需要 f ( π , μ 1 , b 1 , μ 2 , b 2 ) f_{(\pi,\mu_1,b_1,\mu_2,b_2)} f(π,μ1,b1,μ2,b2)函数的回归。而 f ( π , μ 1 , b 1 , μ 2 , b 2 ) f_{(\pi,\mu_1,b_1,\mu_2,b_2)} f(π,μ1,b1,μ2,b2)函数可以很容易地使用神经网络进行表达。
SMD-Nets
backbone
SMD-Nets中backbone的部分可以表达为: Ψ θ : R W × H × 6 → R W × H × D \Psi_{\theta}: \mathbb{R}^{W \times H \times 6} \rightarrow \mathbb{R}^{W \times H \times D} Ψθ:RW×H×6→RW×H×D,
示意图则图下图所示:
实际上就是通用的立体匹配网络。
此时,如果希望能够得到任意分辨率的视差图输出,一种可行的思路为,建立视差图输出的连续表达,即对于每一个连续的2D坐标 x ∈ R 2 \mathbf{x} \in \mathbb{R}^2 x∈R2,我们双线性地在特征图 R W ∗ H ∗ D \mathbb{R}^{W * H * D} RW∗H∗D上,采样得到其最近的四个像素位置的特征,我们不妨将该过程表达为:
ψ : R 2 × R W × H × D → R D \psi: \mathbb{R}^{2} \times \mathbb{R}^{W \times H \times D} \rightarrow \mathbb{R}^{D} ψ:R2×RW×H×D→RD
而对于这样的抽象的特征表达,可以通过MLP的方式将其映射为五维的向量 ( π , μ 1 , b 1 , μ 2 , b 2 ) (\pi,\mu_1,b_1,\mu_2,b_2) (π,μ1,b1,μ2,b2),有了这些参数,就可以定义得到一个单变量的双峰混合分布:
f θ : R D → R 5 f_{\theta}: \mathbb{R}^{D} \rightarrow \mathbb{R}^{5} fθ:RD→R5
注意,在上式中,我们将五维的参数简洁地表示为 θ \theta θ。然而,之后,我们将直接使用 θ \theta θ来表示模型中的所有参数。
SMD-Head
我们将 f θ ( ψ ( ⋅ , ⋅ ) ) f_{\theta}(\psi(\cdot,\cdot)) fθ(ψ(⋅,⋅))命名为SMD Head。
为能够对在不连续处的视差分布进行稳健建模,我们选择双峰拉普拉斯混合分布作为输出,即:
p ( d ) = π 2 b 1 e − ∣ d − μ 1 ∣ b 1 + 1 − π 2 b 2 e − ∣ d − μ 2 ∣ b 2 p(d)=\frac{\pi}{2 b_{1}} e^{-\frac{\left|d-\mu_{1}\right|}{b_{1}}}+\frac{1-\pi}{2 b_{2}} e^{-\frac{\left|d-\mu_{2}\right|}{b_{2}}} p(d)=2b1πe−b1∣d−μ1∣+2b21−πe−b2∣d−μ2∣
整体上来将,SMD-Net可以被简洁地表示为:
p ( d ∣ x , I , θ ) = p ( d ∣ f θ ( ψ ( x , Ψ θ ( I ) ) ) ) p(d \mid \mathbf{x}, \mathbf{I}, \theta)=p\left(d \mid f_{\theta}\left(\psi\left(\mathbf{x}, \Psi_{\theta}(\mathbf{I})\right)\right)\right) p(d∣x,I,θ)=p(d∣fθ(ψ(x,Ψθ(I))))
至于在推理的过程中,我们则直接选择有着最高密度值的那一对参数的分布,并直接取概率最大处所对应的视差,即:
d ^ = argmax d ∈ { μ 1 , μ 2 } p ( d ) \hat{d}=\underset{d \in\left\{\mu_{1}, \mu_{2}\right\}}{\operatorname{argmax}} p(d) d^=d∈{μ1,μ2}argmaxp(d)
通过这样的方式,可以得到任意分辨率的视差图,且在边界上有着非常好的效果,如下图所示:
此外,该模型还可以通过计算该连续混合分布的微分熵来得到不确定度的输出:
h = − ∫ p ( d ) log p ( d ) d d h=-\int p(d) \log p(d) \mathrm{d} d h=−∫p(d)logp(d)dd
在实践中,我们使用数值的方式来得到该积分的近似。
在实现中,SMD Head通过多层感知机的方式进行实现,逐层神经元的数目为:(D, 1024, 512, 256, 128, 5)。最后一层采用的激活函数是sigmoid,其他层采用的激活函数是Sine。
损失函数
文章考虑有监督的设定,进而通过最小化负对数似然的方式进行模型训练,即:
L N L L ( θ ) = − E d , x , I log p ( d ∣ x , I , θ ) \mathcal{L}_{N L L}(\theta)=-\mathbb{E}_{d, \mathbf{x}, \mathbf{I}} \log p(d \mid \mathbf{x}, \mathbf{I}, \theta) LNLL(θ)=−Ed,x,Ilogp(d∣x,I,θ)
其中, I \mathbf{I} I是数据集中的随机采样, x \mathbf{x} x是影像域: Ω = [ 0 , W − 1 ] ∗ [ 0 , H − 1 ] \Omega = [0, W-1] * [0, H-1] Ω=[0,W−1]∗[0,H−1]中的随机位置,具体的采样方式见下一小节, d d d则是在位置 x \mathbf{x} x处的视差真值。
双峰分布的损失函数实现代码:
def gaussian(mu, sigma, labels): return torch.exp(-0.5*(mu-labels)** 2/ sigma** 2)/sigma def laplacian(mu, b, labels): return 0.5 * torch.exp(-(torch.abs(mu-labels)/b))/b def distribution(mu, sigma, labels, dist="gaussian"): return gaussian(mu, sigma, labels) if dist=="gaussian" else \ laplacian(mu, sigma, labels) def bimodal_loss(mu0, mu1, sigma0, sigma1, w0, w1, labels, dist="gaussian"): return - torch.log(w0 * distribution(mu0, sigma0, labels, dist) + \ w1 * distribution(mu1, sigma1, labels, dist))
采样策略
现在设影像域为 Ω \Omega Ω,如果说采样 x \mathbf{x} x的策略是随机采样,或许并不会得到最优的效果,因此SMD在采样方面也做了一些工作,具体指允许能够使得网络训练过程中更专注于在深度不连续的区域的采样方式。
提出了一种深度不连续感知(Depth Discontinuity Aware,简称DDA)的采样方式,该方式显式地倾向于边界区域的像素点,且同时会保持整张图像上均匀的覆盖。具体地,在训练中给定视差图GT,首先计算物体边界的mask,将物体判定为边界的准则是,像素四邻域内有一个以上的视差与自身像素差别大于1。该mask接下来将被使用 ρ ∗ ρ \rho * \rho ρ∗ρ大小的进行边界膨胀,在实验中,对比了不同核大小的膨胀核对结果的影响,并进行了一定程度的分析。
在给定总训练像素点数 N N N的情况下,随机且均匀地从深度不连续区域选择 N / 2 N/2 N/2个点,再从剩余的连续的区域内选择 N / 2 N/2 N/2个点。在推理阶段,模型则可得到任意分辨率、任意位置的视差值。
实验
在本节中,首先对数据集进行介绍,其次,进行了一系列的实验评估,其结果证明了SMD-head部分在不同任务中与不同骨干网络结合的益处。
数据集
使用了一部分作者团队自己制作的数据集(UnrealStereo4K、RealActive4K)以及公开数据集(KITTI 2015、Middlebury v3)。
消融实验
首先验证SMD-Nets中不同组件和训练策略对UnrealStereo4K测试集的影响。
除非另有说明,则默认使用960 x 540分辨率为双目输入 I \mathbf{I} I的分辨率,使用3840 x 2160分辨率为视差图GT。
主动双目输入图像包含了随机的散斑图样,这些散斑显然在低分辨率(例如,960 x 540)下变得难以区分。因此,主动双目的输入分辨率为2056 × 1504,视差图GT为4112 × 3008。
不同的输出表达形式:视差回归、单峰拉普拉斯分布与双峰分布
在Tab 1.中,评估了混合密度输出表示在2D和3D的立体匹配主干网络上的有效性,任务包括双目立体、单眼深度估计和主动深度估计。
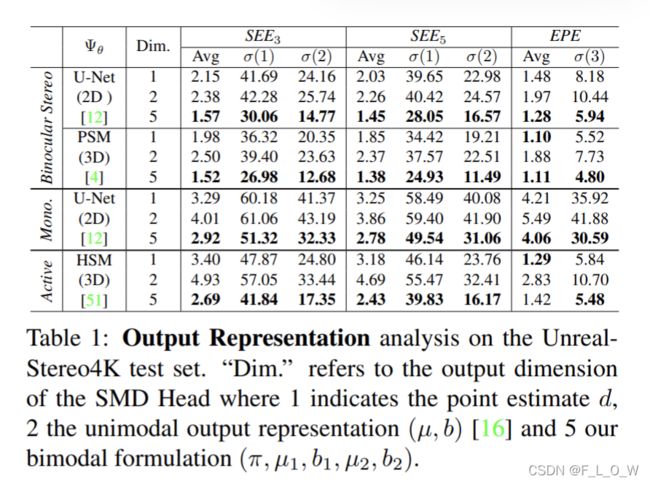
在双目立体数据集上采用U-Net和PSM作为2D和3D主干网络的代表。
此外,使用同样的U-Net主干网络来进行单目深度估计任务,与双目任务相比,唯一的修改在于将双目的输入改为单张影像的输入,这样的实验设置的目的是验证方法在不同任务上的兼容优势。
对于主动深度估计任务,选择HSM网络作为主干网络,原因是HSM是一个专门为高分辨率输入而设计的网络,这样的设计原则适用于主动深度估计任务。其输入为一张参考散斑图与一张散斑场景图。所谓的不同输出表达,在实验中具体指双峰分布、标准视差回归与单峰拉普拉斯分布。
为尽可能保证实验的公平性,仅替换SMD Head的最后一层来分别预测视差 d d d(使用标准L1损失)或单模态参数 μ , b \mu,b μ,b(使用负对数似然损失)。对于不同的输出表达,均采用双线性特征插值以及朴素随机抽样策略。
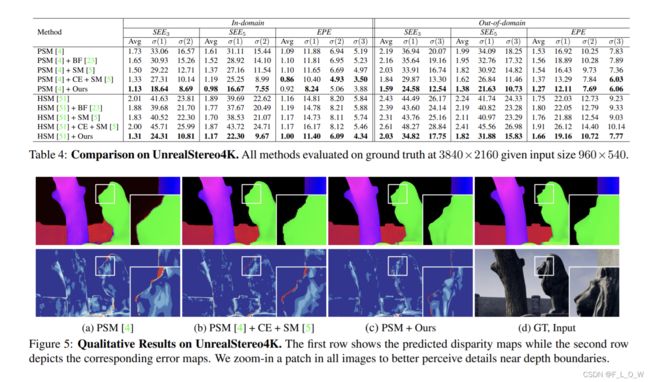
Tab 1表明,所提方法有效地解决了物体边界处的过平滑问题。与标准视差回归和单峰拉普拉斯输出相比,在所有任务中双峰分布都取得了最优的SEE。
此外,可以观察到单峰拉普拉斯分布会牺牲EPE精度来得到不确定性。且在立体数据集上,3D网络(PSM)的性能始终优于2D网络(U-Net),因此在接下来的消融实验中均使用PSM网络作为骨干网络。
不同采样策略
在Tab 2中,体现了不同采样策略对结果的影响:
具体地,比较了朴素均匀采样的策略,和所提出的DDA的采样策略之间的差别。所谓的DDA的采样策略可以使用不同的膨胀核大小,比如说 ρ ∗ ρ \rho * \rho ρ∗ρ,其作用是希望网络能够更专注于深度不连续区域。由表可见,当 ρ \rho ρ为10的时候,整体的效果都会比较好,过大或过小都会相对差一些。特别地,精确地在深度边界(即 ρ = 0 \rho = 0 ρ=0)采样会导致EPE指标轻微的变差。而当 ρ \rho ρ取的比10大的时候,并不会取得更好的效果。
因此,在后续的实验中,都采用核大小为DDA的膨胀核作为采样策略。
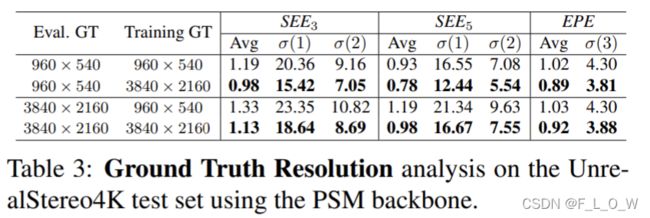
不同视差真值分辨率
Tab 3 表现了模型在立体数据上使用不同分辨率的视差真值进行训练和测试的结果,而其输入尺寸始终为960 x 540。
为了实现不同视差真值分辨率的实验比对,有:
(1)使用最近邻插值将视差真值调整为与输入同分辨率;
(2)原始分辨率(即3840 x 2160)。
由表可见,使用高分辨率视差图GT进行采样的时候总是会得到更好的结果。
与当前Baseline的比较
结论
- 双峰拉普拉斯分布,实现前景与背景的区分,进而得到边缘锐利的视差图;
- 使用连续表达实现超分,超分是一块通用的内容,值得研究。
参考文献
PSM-Net:
Jia-Ren Chang and Yong-Sheng Chen. Pyramid stereo matching network. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2018.
HSM-Net:
Gengshan Yang, Joshua Manela, Michael Happold, and Deva Ramanan. Hierarchical deep stereo matching on highresolution images. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), 2019.