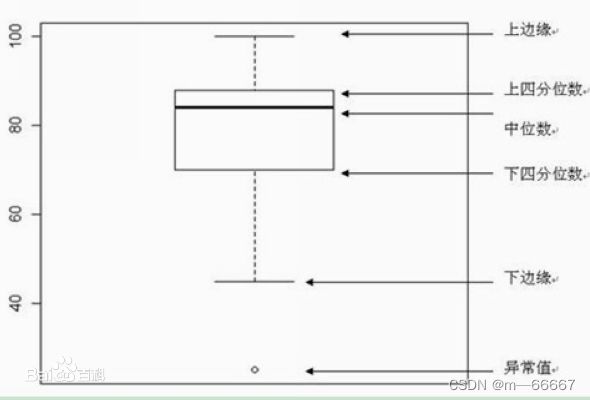
【箱型图】

箱形图（Box-plot）又称为盒须图、盒式图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用，常见于品质管理。它主要用于反映原始数据分布的特征，还可以进行多组数据分布特征的比 较。箱线图的绘制方法是：先找出一组数据的上边缘、下边缘、中位数和两个四分位数；然后， 连接两个四分位数画出箱体；再将上边缘和下边缘与箱体相连接，中位数在箱体中间。

1.箱型图代码

代码如下（示例）：

# 箱型图(箱型图代码拿走不谢)
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel('D:\数据挖掘\财务项目\缺失值填补2.xlsx', )
data=data.iloc[5000:7000,:]
print('输出数据的维度:', data.shape)
# 数据集的描述
print(data.describe())  # count：数量统计，此列共有多少有效值 unipue：不同的值有多少个 std：标准差 min：最小值 25%：四分之一分位数 50%：二分之一分位数 75%：四分之三分位数 max：最大值 mean：均值
# 数据集数据
print('输出前n项数据(默认前5项):')
print(data.head(n=5))
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
df = pd.DataFrame(data)
df.plot.box(title="负债合计")
plt.grid(linestyle="--")
plt.show()

2.改进版

代码如下（示例）：

# 箱型图
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_excel('D:\数据挖掘\财务项目\缺失值填补2.xlsx')
data=data.iloc[5000:7000,:]
print('输出数据的维度:', data.shape)
# 数据集的描述
print(data.describe())  # count：数量统计，此列共有多少有效值 unipue：不同的值有多少个 std：标准差 min：最小值 25%：四分之一分位数 50%：二分之一分位数 75%：四分之三分位数 max：最大值 mean：均值
# 数据集数据
print('输出前n项数据(默认前5项):')
print(data.head(n=5))
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
df = pd.DataFrame(data)
plt.figure()  # 建立图像
data = pd.DataFrame(data, dtype=float)
#data=data/10**np.ceil(np.log10(data.abs().max()))#规范化
p = data.boxplot(return_type='dict')  # 画箱线图，直接使用DataFrame的方法
x = p['fliers'][0].get_xdata()  # 'flier即为异常值的标签-get_xdata()
y = p['fliers'][0].get_ydata()
y.sort()
'''用annotate添加注释，其中相近的点，注释会出现重叠，难以看清，需要一些技巧来控制，以下参数都是经过调试的，需要具体问题具体分析'''
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.05 - 0.8 / (y[i] - y[i - 1]), y[i]))
    else:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.08, y[i]))
plt.show()#展示箱型图

 

这组数据显示出：

• 最小值(minimum)=5

• 下四分位数(Q1)=70

• 中位数(Med--也就是Q2)=80

• 上四分位数(Q3)=90

• 最大值(maximum)=99

• 平均值=80

• 四分位间距(interquartile range)={\displaystyle Q3-Q1}=2 (即ΔQ)

在区间 Q3+1.5ΔQ, Q1-1.5ΔQ 之外的值被视为应忽略(farout)。

• farout: 在图上不予显示，仅标注一个符号∇。

• 最大值区间： Q3+1.5ΔQ

• 最小值区间： Q1-1.5ΔQ

最大值与最小值产生于这个区间。区间外的值被视为异常值显示在图上.

 

总结
 

数据异常值

一批数据中的异常值值得关注，忽视异常值的存在是十分危险的，不加剔除地把异常值包括进数据的计算分析过程中，对结果会带来不良影响；重视异常值的出现，分析其产生的原因，常常成为发现问题进而改进决策的契机。箱形图为我们提供了识别异常值的一个标准：异常值被定义为小于Q1－1.5IQR或大于Q3+1.5IQR的值。虽然这种标准有点任意性，但它来源于经验判断，经验表明它在处理需要特别注意的数据方面表现不错。这与识别异常值的经典方法有些不同。众所周知，基于正态分布的3σ法则或z分数方法是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。它们判断异常值的标准是以计算数据批的均值和标准差为基础的，而均值和标准差的耐抗性极小，异常值本身会对它们产生较大影响，这样产生的异常值个数不会多于总数0.7%。显然，应用这种方法于非正态分布数据中判断异常值，其有效性是有限的。箱形图的绘制依靠实际数据，不需要事先假定数据服从特定的分布形式，没有对数据作任何限制性要求，它只是真实直观地表现数据形状的本来面貌；另一方面，箱形图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不能对这个标准施加影响，箱形图识别异常值的结果比较客观。由此可见，箱形图在识别异常值方面有一定的优越性。

---