【考研】830 + 848 暨大2012-2022真题易混易错题总结（二）

前言

以下题目，均源自于暨南大学 2012 - 2022 年的 830 + 848 真题。主要是对真题中易混易错题进行记录和总结。

分为三篇博文，此乃第二篇，真题是 2018 - 2020 年的，即 830 的有 2018 - 2020 年的 ，还有 2020年 的 848。（2021-2022 待补充）

可搭配以下链接一起学习：

【考研】830 + 848 暨大2012-2022真题易混易错题总结（一）_住在阳光的心里的博客

【考研】《数据结构》知识点总结.pdf_考研-其它文档类资源-CSDN文库

【2023考研】数据结构常考应用典型例题（含真题）_住在阳光的心里的博客-CSDN博客

此文免费阅读，欢迎点赞 + 收藏 + 评论。（如有错误，请指正。）

目录

前言

一、暨大 2018 - 2020 真题（830 + 848 数据结构部分）

二、暨大 2020 - 848 操作系统部分

---

一、暨大 2018 - 2020 真题（830 + 848 数据结构部分）

1、顺序栈 s 的 GetTop(s, e) 操作是用 e 返回 s 的栈顶元素，则下列(  AB  )是正确的操作。

A.  e = *(s.top)              B.  e = *(s.top-1)              C.  e = *(--s.top)             D.  e = s.top-1

解： 此题答案有争议，因未说明栈顶指针初始化时的值，所以 AB 选项都是正确的。

当初始化 top = -1，选 A；初始化 top = 0，选 B。

见下表：

初始化栈顶指针	进栈操作	出栈操作	top 指向
S.top = -1	S.data[++S.top] = x;	x = S.data[S.top--];	栈顶元素
S.top = 0	S.data[S.top++] = x;	x = S.data[--S.top];	栈顶元素的下一位置

2、 若线性表最常用的操作是存取第 i 个元素及其前趋的值，则采用(  D )存储方式节省时间.

A. 单链表               B. 双链表                 C.  单循环链表               D.  顺序表

解：顺序表的存储结构支持随机存取，方便。

3、若用单链表来表示队列，最适合队列操作的是（   B   ）。

A. 带尾指针的非循环队列                         B. 带尾指针的循环链表

C. 带头指针的非循环链表                        D. 带头指针的循环链表

解：循环链表可防止假溢出。

带尾指针的循环链表，能在O(1)时间内找到队首和队尾，方便插入删除操作。

D项：当指带头指针的循环单链表时，进行删除操作时，需要从头遍历到尾，复杂度O(n)，所以不是最适合队列操作。

如果把 D 项改为只带头指针的循环双链表，或只带尾指针的循环双链表，均能在O(1)时间内找到队首和队尾，也是适合队列操作的。

4、用带头结点的单链表存储队列，其队头指针指向头结点，队尾指针指向队尾结点，则在进行出队时（     D    ）。

A. 仅修改队头指针                                    B. 仅修改队尾指针

C. 对头、尾指针都要修改                         D. 对头、尾指针都可能要修改

解：队列用链式存储时，删除元素从表头删除，通常仅需修改头指针，一般会误选 A 选项，而忽略了一种可能存在的情况：当链表仅有一个元素时，头、尾指针都要修改。

5、对线性表进行折半查找时，要求线性表必须顺序存储且关键字有序。

6、在中序线索二叉树上，若当前访问节点的右标志为0，根据中序遍历的定义，它的后继结点是     该结点右子树中最左下结点      。

解：（1）寻找结点后继：如果 RTag = 1，直接找到后继，如果 RTag = 0，则走到该结点右子树的最左边的结点，即为要寻找的结点的前驱。

（2）寻找结点前驱：如果 LTag = 1，直接找到前驱，如果 LTag = 0，则走到该结点左子树的最右边的结点，即为要寻找的结点的前驱。

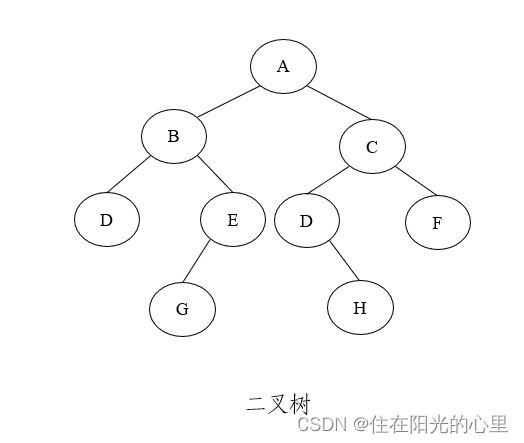
举例：随便找一张二叉树图来理解：

可知该二叉树的中序遍历是 DBGEADHCF。

如果要找结点 B 的后继，由中序遍历结果可知是结点 G，即该结点右子树中最左下结点。如果要找结点 C 的前继，由中序遍历结果可知是结点 H，即该结点左子树的最右边的结点。

可搭配以下链接一起学习：

【考研】数据结构——线索二叉树_住在阳光的心里的博客-CSDN博客

7、对于含有 n 个顶点 e 条边的无向连通图, 利用广度优先搜索遍历图的时间复杂度为  或  。

解：见下表：

n 个顶点 e 条边的无向连通图	广度优先搜索遍历	深度优先搜索遍历
邻接矩阵
邻接表

8、Dijkstra 算法是按     路径长度递增      次序产生一点到其余各定点最短路径的算法。

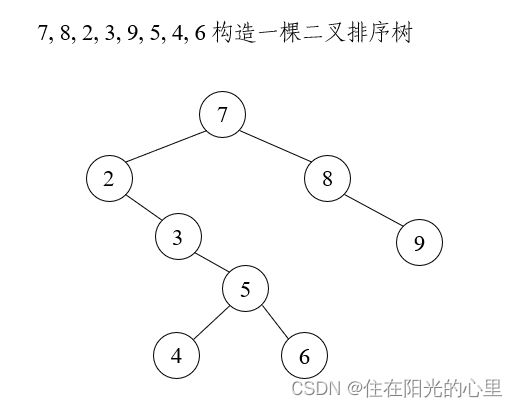
9、一个无序的元素序列可以通过构造一棵二叉排序树而变成一个有序的元素序列。（对）

解：如下图：

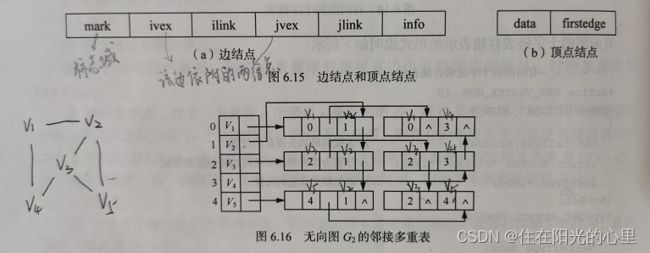
10、图的多重邻接表表示法中，表中结点的数目是图中边的条数。 （对）

 解： 用下图来理解这句话，就明白了：

11、对于有向无环图，除了可以用拓扑排序的方法求出有向图的所有拓扑序列，还可以采用深度优先遍历算法来获得。

 解：深度优先遍历过程中，顶点退栈的顺序是逆拓扑序列。

例如：对有向图：, , , ，拓扑序列可以是 ACBD。

从 A 开始进行 DFS，A 入栈 S，此时 S = {A}；再 B 入栈，S = {A, B}，再 D 入栈，S = {A, B, D}

然后，D 出栈，S = {A, B}，B 出栈，S = {A}，再 C 入栈，S = {A, C}

再 C 出栈，S = {A}；A 出栈，S = {}

此时，元素出栈序列为 DBCA，是拓扑序列可以是 ACBD 的逆序列。

12、设计算法，对 n 个关键字取实数值的记录序列进行整理，以使所有关键字为负值的记录排序在非负值的记录之前（要求尽量减少记录的交换次数）。

解：代码如下：

void Divide(int a[], int n){
    int pivot = a[low];
    low = 0;
    high = n-1;
    while(low <= high){
        while(a[high] >= 0)
            high--;    //以 0 作为虚拟的枢轴记录
        a[low] = a[high];
        while(a[low] < 0)
            low++;
        a[high] = a[low];
    }
    a[low] = pivot;
}

13、试编写出一个判别表达式中左、右小括号是否配对出现的算法。

解：（1）算法思想：本题主要是考察栈的应用，当遇到左小括号时，则需要进栈操作，当是遇到右括号时，则进行出栈操作。最后当栈为空时，则匹配，否则不匹配。

（2）代码如下：

bool Parenthesis_match(sqstack *s, char *str){		
    int i = 0, flag = 0;		
    SElemtype e;		
    while(str[i] != '\0'){	
	    switch(str[i]){				
		    case '(': push(s, str[i]);	break;           
            case ')': { 
				pop(s, &e);
                if(e != '(')
                    flag = 1;
            }
		    break;
		    default: break;
	    }
		if(flag)
			break;			
		i++;	
	}    
	if(!flag && stackempty(s)){	
		printf("括号匹配成功!\n");
		return true;
	}  
	else{
		printf("括号匹配失败!\n");   
		return false;
	}
}

（3）补充：判断表达式括号是否匹配（完整算法）

#include
#include
using namespace std;
#define MaxSize 20
//字符串栈
class Stack
{
    char *data;
    int top;
public:
    Stack();
    ~Stack();
    bool IsEmpty();
    bool Push(char e);
    bool Pop(char& e);
};

Stack::Stack()
{
    data = new char[MaxSize];
    top = -1;
}

Stack::~Stack()
{
    delete [] data;
}

bool Stack::IsEmpty()   //判断栈空
{
    return (top == -1);
}

bool Stack::Push(char e)  //入栈
{
    if(top == MaxSize-1)    return false;   //栈满
    top++;
    data[top] = e;
    return true;
}

bool Stack::Pop(char& e)  //出栈
{
    if(top == -1)   return false;   //栈空
    e = data[top];
    top--;
    return true;
}

bool IsMatch(char str[],int n)  //判断表达式括号是否匹配
{
    int i = 0;
    char e;
    Stack st;   //建立顺序栈
    while(i < n)
    {
        if(str[i] == '(' || str[i] == '[' || str[i] == '{')
            st.Push(str[i]);
        else
        {
            if(str[i] == ')')
            {
                if(!st.Pop(e))  return false;
                if(e!='(')  return false;  //如果弹出的元素e不是与）对应的（，则返回false。
            }
            if(str[i] == ']')
            {
                if(!st.Pop(e))  return false;
                if(e!='[')  return false;
            }
            if(str[i] == '}')
            {
                if(!st.Pop(e))  return false;
                if(e!='{')  return false;
            }
        }
        i++;
    }
    if(st.IsEmpty())    return true;    
    else return false;  //遍历字符串后栈不为空说明有不匹配字符
}

void main()
{
    cout<<"请输入表达式："<>str;
    int n = strlen(str);

    if(IsMatch(str, n))
        cout<<"表达式"<< str <<"中的括号是匹配的"<

代码源自以下链接：

常见算法题：判断表达式括号是否匹配_至浊至愚的博客-CSDN博客

还可以搭配以下链接学习：

【考研】栈在表达式求值中的应用（真题分析）_住在阳光的心里的博客-CSDN博客

14、假设二叉树采用二叉链存储结构存储，试编写一个非递归算法，输出先序遍历序列中第 k 个结点的数据值。

解：代码如下：

//用人工栈，先序遍历（非递归），输出先序遍历序列中第 k 个结点的数据值
void preorder_nonrecursion_k(BiTNode *bt, int k){
    if(bt != nullptr){
        BiTNode *stack[MaxSize];
        int top = -1;
 
        stack[++top] = bt;    //栈顶指针加一，根结点入栈
        BiTNode *p;
 
        while(top != -1){  //判断栈不为空
            p = stack[top--];    //出栈，栈顶指针减一
            count++;
            
            if(count == k){
                printf("%d", p->data);
            }
 
            if(p->rchild != nullptr){   //栈是先进后出，所以一定是先遍历右孩子，再左孩子
                stack[++top] = p->rchild;
            }
 
            if(p->lchild != nullptr){   //遍历左孩子
                stack[++top] = p->lchild;
            }
        }
    }
}

可以看看非递归的先序遍历算法：

//用人工栈，先序遍历（非递归）
void preorder_nonrecursion(BiTNode *bt){
    if(bt != nullptr){
        //定义人工栈
        BiTNode *stack[MaxSize];
        int top = -1;
 
        stack[++top] = bt;    //栈顶指针加一，根结点入栈
        BiTNode *p;
 
        while(top != -1){  //判断栈不为空
            p = stack[top--];    //出栈，栈顶指针减一
            printf("%c\n", p->data);
 
            if(p->rchild != nullptr){   //栈是先进后出，所以一定是先遍历右孩子，再左孩子
                stack[++top] = p->rchild;
            }
 
            if(p->lchild != nullptr){   //遍历左孩子
                stack[++top] = p->lchild;
            }
        }
    }
}

可搭配以下链接一起学习：

【考研】常考的二叉树相关算法总结（详细全面）_住在阳光的心里的博客-CSDN博客

15、设输入元素1,2,3,P,A，输入次序为：123PA，元素经过栈后到达输出序列。当所有元素均达到输出序列，下面（    B    ）序列可以作为高级语言的变量名。

A. 123PA                             B.  PA321                    C. 12AP3                 D. PA123

解：排除 D 选项，是因为它不是栈的输出序列。

在定义高级语言的变量名时，变量名可以是字母、数字和下划线的组合。但要注意以下几个命名规则：

（1） 变量名的开头必须是字母或下划线，不能是数字。实际编程中最常用的是以字母开头，而以下划线开头的变量名是系统专用的。（所以，排除A、C选项。所以，选B。）

（2）变量名中的字母是区分大小写的。

（3） 变量名绝对不可以是C语言关键字。

（4）变量名中不能有空格。

16、在一个链队列 Q 中，删除一个结点需要执行的指令是（    C    ）。

A.  Q.rear = Q.front->next;                               B.  Q.rear->next = Q.rear->next->next;

C.  Q.front->next = Q.front->next->next;          D.  Q.front = Q.rear->next;

解：出队操作代码如下：

//出队
void DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front == Q.rear)   //队空则报错
        return false;    
 
    LinkNode *p = Q.front->next;
 
    x = p->data;
    Q.front->next = p->next;
    if(Q.rear == p)
        Q.rear = Q.front;    //若原队列只有一个结点，删除后变空
    free(p);
 
    return true;
}

可见下方链接：

【考研】栈和队列基础算法代码_住在阳光的心里的博客-CSDN博客

17、在一个 3 阶的 B- 树上，每个结点包含的子树相同，最多为            个结点，最少为              个结点。

解：3 阶的 B- 树上，每个结点包含的子树相同，所以：

（1）求最多结点时，每个结点都有 3 棵子树。

（2）求最少结点时，每个结点都有 2 棵子树，从下图可知，此时相当一棵满二叉树。

对比满二叉树和完全二叉树，可以举个例子来直接推导：

 公式：

（1）度为 m 的树中，第 i 层至多有  个结点（i >= 1）（可推出三叉树第4层有27个结点）

（2）高度为 h 的 m 叉树中，至多有  个结点。（这个直接推出本题第一个填空处）

18、对于一个具有 n 个顶点的无向连通图，它包含的连通分量的个数为（   B    ）。

A．0                  B．1                     C．n                      D．n+1

解：一个无向图连通图，即为一个连通分量。

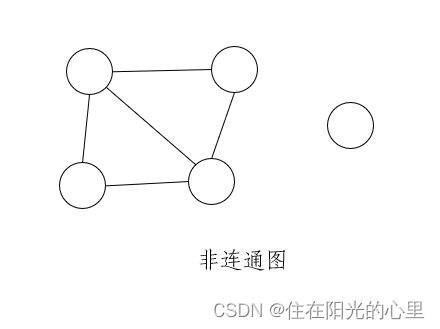
19、在 n 个顶点的无向图中，若边数 > n-1，则该图必是连通图。（  错  )

解：见下图：

20、完全二叉树的某结点若无左孩子，则必是叶子结点。 （  对  )

21、用邻接矩阵法存储一个图时，在不考虑压缩存储的情况下，所占用的存储空间大小与图中结点的个数有关，而与图的边数无关。（  对  )

22、【简答题】设 G 为有 n 个顶点的无向连通图，证明 G 至少有 n - 1  条边。 （7分）

证明1：

假设使用 n - 1 条无向边可以使得含有 n 个顶点得无向图连通。

① 当 n = 1 时，成立。

② 设当 n = k 时，使用 k - 1 条无向边可以使得无向图连通。

③ 当 n = k + 1 时，因为 k - 1 条无向边可以使得 k 个顶点连通，则无向图 G 有 k + 1 个顶点，使用 k - 1 条无向边将 k 个顶点连通后，无向图 G 有两个连通分量，从两个连通分量中各取一个顶点建立一条无向边则使得整个图连通，即使用 k 条无向边可以使得含有 n 个顶点的无向图连通，成立。

又因为一条边仅可以连接两个顶点，故当无向图 G 的顶点数为 n，显然 n - 2 条无向边无法使得无向图连通。

由此可得，G 为有 n 个顶点的无向连通图至少有 n - 1 条边证明成立。

证明2：

设连通图 G 有（n + 1）个顶点，若每个顶点连出至少两条边，那么此时至少有 n + 1 条边（任意图上所有顶点度数和等于边数的两倍），结论已经成立。

否则，那么至少有一个顶点只连出一条边。由于去掉这条边后不影响其他点的连通性，那么剩下的 n 个点之间有归纳假设至少有（n - 1) 条边，所以 G 至少有 n - 1 条边。

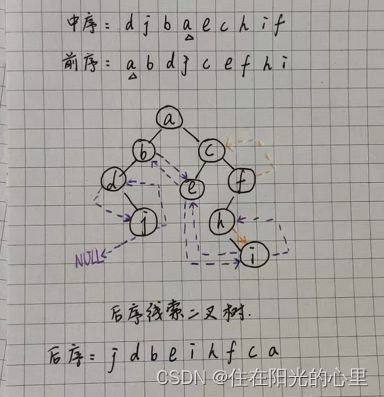
23、什么是线索二叉树？一棵二叉树的中序遍历序列为djbaechif，前序遍历序列为abdjcefhi,请画出该二叉树的后序线索二叉树。

解：规定若无左子树则令 lchild 指向其前驱结点；若无右子树，则令 rchild 指向其后继结点，还需要增加两个标志域标识指针域是指向左右孩子还是指向前驱后继，以这种结构构成的二叉链表作为二叉树的存储结构，成为线索链表，加上线索的二叉树称为线索二叉树。

该二叉树的后序线索二叉树见下图：（用不同颜色的笔画的虚线以辨别）

24、给定一棵二叉链表存储的二叉树，试用文字描述判定一棵二叉树是否是完全二叉树的算法基本思想。（7分）

解：先对二叉树按入队规则先左子树后右子树进行广度优先遍历，并且再遍历过程中按出队顺序由1开始进行连续编号。之后再对该二叉树继续进行一次广度优先遍历，遍历过程中若出现：

（1）当前出队的结点存在左结点，且左结点的编号不是当前结点编号的两倍；

（2）当前出队的结点存在右结点，且右结点的编号不是当前结点编号的两倍加一时，该二叉树不是完全二叉树，若遍历完成后均符合要求，则证明该二叉树为完全二叉树。

25、试编写算法，从大到小输出二叉排序树中所有的值不小于 x 的关键字。

解：（1）算法思想： 二叉排序树满足 “左子树的值 < 根结点的值 < 右子树的值”，所以，要想输出的值从大到小依次排列，应该依次遍历右子树、根结点、左子树。

（2）代码如下：

typedef struct BitTree{
    int data;
    struct BitTree *lchild, *rchild;
};

void printBt(BitTree &p){
    if(!p) return;
    if(p->data < x) printBt(p->rchild);
    else{
        printBt(p->rchild);           //遍历右子树
        printf("%d ", p->data);         //打印关键字
        printBt(p->lchild);           //遍历左子树
    }
}

可搭配以下链接学习：

【考研】常考的二叉树相关算法总结（详细全面）_住在阳光的心里的博客-CSDN博客

26、设有一个由正整数组成的无序单链表，试编写算法实现下列功能：

（1）找出最小值结点，并输出该数值；

（2）若该最小值是奇数，则将其与直接后继结点的数值交换；如该最小值是偶数，则将其直接后继结点删除。

解：代码如下：

typedef struct ListLink{
    int data;
    struct ListLink *next;
};

void solve(ListLink &L){
    ListLink *p = L;    // L 为带头结点的单链表
    if(!p) return;
    ListLink *r = p->next; // r 用来存放最小值结点
    int min = r->data;

    while(p->next != NULL){
        p = p->next;
        if(p->data < min){
            min = p->data;
            r = p;
        }
    }
    printf(r->data);   //找出最小值结点，并输出该数值；

    if(r->data & 1){  //判断 r 是不是奇数，是就与直接后继结点的数值交换
        if(r->next != NULL){
            int t = r->next->data;
            r->next->data = r->data;
            r->data = t;
        }
    }
    else{   //若是偶数，则将其直接后继结点删除
        if(r->next!=NULL){
            p = r->next;
            r->next = r->next->next;
            free(p);
        }
    }
}

【补充】

判断某整数 num 是奇数还是偶数， 有两种方法：（方法二比方法一快）

（1）num % 2 == 0，则为偶数； 否则为奇数；

（2）用按位与，即 num & 1，值为 1 则为奇数，值为 0 则为偶数。

C / C++ 中的 “ 按位与 ”规则：1 & 1 = 1，1 & 0 = 0，0 & 1 = 0，0 & 0 = 0。

举例：8 & 1 = 1000 & 0001 = 0000；7 & 1 = 0111 & 0001 = 0001

27、编写一个算法根据用户输入的偶对（以输入0表示结束）建立其有向图的邻接表（设有n个顶点）。

解： 代码如下：

//根据用户输入的偶对（以输入0表示结束）建立其有向图的邻接表（设有n个顶点）
typedef struct LinkNode{
    int v;
    struct LinkNode *next;
};

typedef struct ListLink{
    LinkNode *list;
    LinkNode *tail;
};

void solve(ListLink L[], int n){
    for(int i = 1; i <= n; i++){
        L[i].list = (LinkNode *)malloc(sizeof(LinkNode));
        L[i].list->next = NULL;
        L[i].tail = L[i].list;
    }

    int v, u;
    while(scanf("%d", &u)){
        if(u != 0) scanf("%d", &v);
        else break;

        LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode));
        p->v = v;
        p->next = NULL;

        L[u].tail->next = p;
        L[u].tail = p;
    }
}

28、 哈希表的平均查找长度说法错误的是 (     B    )。

A. 与处理冲突方法有关而与表的长度无关                   B. 与选用的哈希函数有关

C. 与哈希表的饱和程度有关                                        D. 与表中填入的记录数有关

解：此题博主认为答案不太严谨，若选用个很好的哈希函数（“均匀的”），那么产生冲突的可能性相同，平均查找长度则与哈希函数无关。

在《数据结构》教材中，有这么一段话：在一般情况下认为：凡是“均匀的”散列函数，对同一组随机的关键字，产生冲突的可能性相同，假如所设定的散列函数是“均匀”的，则影响平均查找长度的因素只有两个——处理冲突的方法和哈希表的装填因子。

装填因子 = 表中填入的记录个数 / 哈希表的长度，装填因子标志散列表的装满程度。若散列表表长足够长，通过哈希函数得到的地址能无冲突分散在表中，与表长也是有关的。（但查了下，说是教材默认与表长无关的？）

29、 一棵完全二叉树上有 3001 个结点，其中叶子结点的个数是（    B    ）。

A. 1500                           B.1501                         C. 1000                          D.1001

解： 设度为 0、1、2 的结点数为 x、y、z。

已知 x = z + 1，完全二叉树中 y 的取值只能为 0 或 1。

所以，2z + y + 1 = 3001，得 2z + y = 3000，可知 y = 0，所以 z = 1500

所以，叶子结点个数 x = z + 1 = 1501。

【拓展】

（1）一个具有 1025 个结点的二叉树的高 h 为 （     C    ）

A. 10                  B.11               C. 11至1025之间                  D.10至1024之间 

 解：由公式最小树高 

莫忽略了还有单支树的情况，即每层只有一个结点，可知此时树高为结点总数 1025。

（2）得用二叉链表存储树，则根结点的右指针（     C    ）

A. 指向最左孩子                B.指向最右孩子               C. 为空                  D.非空

解： 二叉链表中，右指针是指向兄弟结点的，但由于根结点没有兄弟结点，所以根结点的右指针为空。

30、 在顺序表中插入一个元素，需要平均移动表中一半元素，具体移动元素的个数与

          插入元素在表中的位置       有关。

 31、试编写一个算法完成下面的功能：对于输入的任意一个非负十进制整数，输出与其等值的八进制数。（10分）

解： 代码如下：

#include 
#include 

int main(){
    int n, temp, result;
    SqStack S;
    InitStack(&S);    //初始化栈S
    scanf("%d", &n);

    while(n != 0){
        temp = n % 8;
        Push(&S, temp);   //进栈
        n = n / 8;
    }
    while (S.top - S.base > 0){  //栈不为空
        result = Pop(&S);    //出栈
        printf("%d ”, result);
    }
    printf("\n");
    return 0;
}

32、试编写一个算法，在有向图 G 中，判定从顶点 Vi 到顶点 Vj 是否有通路。（10分）

解： 代码如下：

int visited[MAXSIZE];  //指示顶点是否在当前路径上
int level = 1://递归进行的层数

//深度优先判断有向图 G 中顶点 i 到顶点 j 是否有路径, 是则返回 1, 否则返回 0
int exist_path_DFS(ALGraph G, int i, int j){
    if(i == j) return 1;    // i 就是 j
    else{
        visited[i] = 1;    //标记已访问
        for(p = G.vertices[i].firstarc; p; p = p->nextarc, level--){
            level++;
            k = p->adjvex;
            if(!visited[k] && exist_path(k, j)) return 1;    // i 下游的顶点到 j 有路径
        }
    }
    if(leve1 == 1) return 0;
}

可搭配以下链接一起学习：

【考研】图的相关应用算法考点（详细全面，含真题）_住在阳光的心里的博客

33、用单向链表来实现容量为n的堆栈时，链表头指针指向堆栈顶部元素，链表尾指针指向堆栈底部元素，则以下说法错误的是(     C    )

A. 入栈操作的复杂度为O(1)                   B. 出栈操作的复杂度为O(1)   

C. 删除底部元素的复杂度为O(1)           D. 插入一个新的堆栈底部元素复杂度为O(1)

解： 针对 C 项，删除底部元素需要找到倒数第 2 个元素，遍历时间为 O(n)，而 A、B 选项均只要移动头指针就行，D 项只需要移动尾指针。

34、 若线性表最常用的操作是增加或者删除某个元素, 则采用(    B    )存储方式节省时间。

A. 单链表         B. 双链表         C.  单循环链表     D.  顺序表

解： 单链表删最后一个元素需要遍历整个链表，顺序表不适合频繁插入删除。针对 A、B 选项，博主找到了一个解释很好的答案，如下：

• 单向链表要删除某一节点时，必须要先通过遍历的方式找到前驱节点（通过待删除节点序号或按值查找）。若仅仅知道待删除节点，是不能知道前驱节点的，故单链表的增删操作复杂度为O(n)。

• 双链表（双向链表）知道要删除某一节点p时，获取其前驱节点 q 的方式为 q = p->prior，不必再进行遍历。故时间复杂度为O(1)。而若只知道待删除节点的序号，则依然要按序查找，时间复杂度仍为O(n)。

• 单、双链表的插入操作，若给定前驱节点，则时间复杂度均为O(1)。否则只能按序或按值查找前驱节点，时间复杂度为O(n)。

• 双链表本身的结构优势在于，可以 O(1) 地找到前驱节点，若算法需要对待操作节点的前驱节点做处理，则双链表相比单链表有更加便捷的优势。

• 源于链接：双链表的删除和插入的时间复杂度

35、为了提高哈希表的查找效率，以下方法说法不正确的是(     B     )。

A.  设计好的哈希函数                  B. 增加哈希函数的个数         

C.  增大存储空间                         D. 采用更好的地址冲突解决方法

解： 哈希表的查找效率与 B 选项无关（没有 B 选项这个说法）。

C项，可以理解为哈希表的查找效率与散列因子有关，而增大存储空间，即增大散列表长度，即散列因子越小，哈希表的查找效率越高。

（散列因子 = 表中填入的记录数 / 散列表的长度）

【补充】这一题可以结合前面的第 28 题一起来看。

36、在一个双向链表中，当删除结点 p 时，错误的操作序列为 (     A    )。

A.  p = p->prev; p->next->prev = p; p->next = p->next->next;      

B.  p = p->next; p->prev = p->prev->prev; p->prev->next = p; 

C.  p->prev->next = p->next; p->next->prev = p->prev; 

D. p = p->prev; p->next = p->next->next; p->next->prev = p;

解：针对 A 选项，第二步 p->next->prev = p无意义。

可以看下面画的图：

37、在管理城市道路交通网络据时，最适合采用（    A    ）数据结构来对其进行存储。

A．有向图       B．无向图          C．树           D．矩阵

解：在 《数据结构》（严蔚敏著）中，可见下图：

“交通网往往用带权有向图来表示”，以课本为准，所以选A。

38、对 n 个不同的排序码进行冒泡排序，在元素无序的情况下比较的次数为   n(n-1)/2  。

解：冒泡排序，在最坏的情况下，即待排序元素无序，总的关键字比较次数为  n(n-1)/2  ；记录移动次数为__3n(n-1)/2__。

39、哈希表查找效率高，当查找主键在范围 [a,b] 内所有的记录时，也应该优先选择哈希表。(   错   )

解：关键在所有记录，如果是查所有记录，则可直接用顺序查找，查找一遍就结束。

40、贪婪算法有时候能够求出全局最优解，有时候无法求出全局最优解。(   对   )

41、对 n 个记录进行插入排序，最多只需要 O(nlog(n)) 次两两比较。(  错   )

解：对 n 个记录进行插入排序，最多只需要 n(n - 1)/2 次两两比较。

42、 对 22 个记录的有序表作折半查找，当查找失败时候，至多需要比较    5    次关键字，至少需要比较     4    次关键字。

 解：比较的关键次数 x 满足：折半查找判定树高 - 1 <= x <= 折半查找判定树高

折半查找判定树高  

所以，当查找失败时候，至多需要比较 5 次关键字，至少需要比较 4 次关键字。

43、G 是一个非连通无向图，共有 28 条边，则该图至少有             个顶点。

 解：8 个顶点的无向完全图有 n*(n-1)/2  = 28 条边，得出 n = 8，但由于是非连通图，所以有另外一个顶点，共 9 个。
 

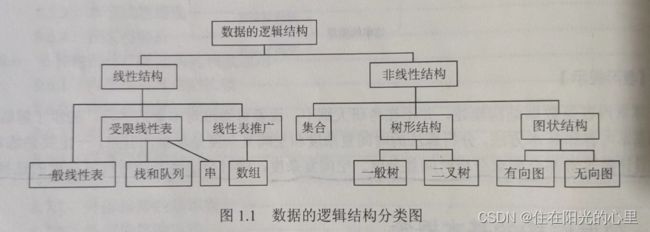
44、简述逻辑结构的四种基本关系并画出它们的关系图。（10分）

 解：(1) 集合，元素间没有关系。

(2) 线性结构，一对一。

(3) 树形结构，一对多。

(4) 图形结构，多对多。

45、设二维数组 num[1….m, 1…n]含有m*n个整数，请分析判断数组中元素是否互不相同的算法的时间复杂度。

 解：(1) 第一种方法：

直接遍历比较，第一个与剩下的 m*n - 1 个比较，第二个与剩下的 m*n - 2 个比较，若互不相同，则比较次数为 (m*n - 1 + 1)*(m*n - 1) / 2，时间复杂度为 。

(2) 第二种方法：

先进行排序，将二维数组所有元素复制到一个长为 m*n 的新数组中，再进行堆排序，排序时间复杂度为 ，排序完从头开始遍历，若每个元素都与其前面的元素不相同，则数组
所有元素互不相同，遍历时间复杂度为 ，总时间复杂度为。

46、写一个算法统计在输入字符串中各个不同字符出现的频度并将结果存入文件（字符串中的合法字符为 A - Z 这 26 个字母与 0 - 9 这 10 个数字）。

 解：算法代码如下：

//统计在输入字符串中各个不同字符出现的频度并将结果存入文件
#include
#include
#include
#include
using namespace std;

const int maxn = 36;
int cnt[maxn];

void solve(char *s){
    int len = strlen(s);
    for(int i = 0; i < len; i++){
        if('0' <= s[i] && s[i] <= '9'){
            cnt[s[i] - '0'] += 1;    
        }
        else if('A' <= s[i] & s[i] <= 'Z'){
            cnt[s[i] - 'A' + 10] += 1;   //加 10 是因为前 10 个存储的是数字
        }
    }

    ofstream ofile;
    ofile.open("./myfile.txt");   //打开文件

    for(int i = 0; i < 10; i++){
        ofile << char(i + '0') << ":" << cnt[i] << endl;    //输出数字及其出现的频度
    }
    for(int i = 10; i < 36; i++){
        ofile << char(i + 'A'- 10) << ":" << cnt[i] << endl;   //输出字母及其出现的频度
    }
    ofile.close();   //关闭文件
}

int main(){
    char s[] = "IVONDSVNOEIBNNCDWIOP0HF130HH280F02CHOG2HV0J2H08GVH02EJ0" ;
    solve(s);
    return 0;
}

47、已知 f 为单链表的表头指针，链表中存储的都是整型数据，请写出实现下列运算的递归算法，求（1）链表中最大整数；（2）所有整数的平均值。

 解：算法代码如下：

//第一种方式
typedef struct LNode{
    int data;
    struct LNode *next;
}LNode, *LinkList;

int n = 0;   //全局变量存放链表长度
int tmpe;

int MAX(LinkList &L){
    if(!L->next) //遍历完整个链表
        return L->data; 

    int m = MAX(L->next);   //递归调用
    if(m > L->data)    //从后往前两两比较，一直存放着从后往前退出递归时的最大值
        return m;
    else
        return L- >data;
}

double AVERAGE(LinkList &L) {
    if(!L->next){ //遍历完整个链表
        tmp = n + 1;//存放结点个数
        return L->data; 
    }

    n++;   //记录链表长度
    double aver = AVERAGE(L->next);
    if(n > 1) {    //退递归直到递归栈栈底
        --n;
        return aver + L->data; //求和
    }
    else 
        return (aver + L- >data) / tmp ;
}

int main() {
    LinkList L;
    struct LNode *f; 
    int max = MAX(f->next); //最大值
    double average = AVERAGE(f->next); //平均值
}

//第二种方法
#include
#include
using namespace std;
const int inf = 0x3f3f3f3f;

struct node{
    int data;
    struct node next;
};

struct node *m = new node();

int getMax(struct node *p){
    if(p->next == NULL){ 
        return p->data;
    }
    else{ 
        return max(getMax(p->next), p->data);
    }
}

int solve1(struct node *m){
    if(m->next == NULL) 
        return -inf;    //-inf表示链表为空
    else return getMax(m->next);
}

int cnt = 0;

int getSum(struct node *p){
    if(p == NULL) return 0;
    cnt += 1;
    return getSum(p->next) + p->data;
}

double solve2(struct node *m){
    if(m->next == NULL) return -inf; //-inf表示链表为空
    else return 1.0 * getSum(m->next)/cnt;
}

48、采用邻接表存储结构，编写一个算法，判别无向图中任意给定的两个顶点之间是否存在一条长度为 k 的简单路径。

解：（1）算法思路：设给定 i,  j 两个顶点。第一步：先写出邻接表的结构体；第二步：以 i 点为源点开始对 i 的边表进行深度优先遍历。

深度优先遍历：遍历时需要对路径的权进行累加，当遍历到 j 点时路径长不等于 k 或累加路径长大于 k 时，返回上一个顶点，并将 j 点的访问标记置为 0 (当置 1 时表示已访问过)，当进行完深度优先遍历时未找到符合条件路径，则路径不存在。

（2）算法代码：

int visitedDMAXSIZE];

//判断邻接表方式存储的有向图 G 的顶点 i 到 j 是否存在长度为 k 的简单路径
int exist_path_len(ALGraph G, int i, int j, int k){
    if(i == j && k = 0) return 1; //找到了一条路径，且长度符合要求
    else if(k > 0){
        visited[i] = 1; .
        for(p = G.vertices[i].firstarc; p; p = p->nextarc){
            w = p->adjvex; .
            if(!visited[w])
                if(exist_path_len(G, w, j, k-1)) return 1; //剩余路径长度减1,
        }
        visited[i] = 0;
    }
    return 0;
}

二、暨大 2020 - 848 操作系统部分

1、文件系统采用树形目录结构可以节省内存空间。（  对 ）

2、在作业调度时，采用最高响应比优先的作业调度算法可以得到最短的作业平均周转时间。  （  错 ）

解： 最短作业优先算法（SJF）可以得到最短的作业平均周转时间。

3、对于速率为 9.6KB/s 的数据通信而言，如果设置一个具有 8 位的缓冲寄存器，则 CPU 中断时间和响应时间分别大约为      0.8ms     、     0.1ms    。

解： （1）CPU 中断时间：

（2）CPU 响应时间：

4、在具有 n 个进程的系统中，允许 m 个进程 (n ≥ m ≥ 1) 同时进入它们的临界区，其信号量 S 的值的变化范围是   [m - n, m]   ，处于等待状态的进程数最多有   n - m  个。

解：从物理概念上讲，信号量 S > 0 时，S 值表示可用资源数量。当 S < 0  时，表示已无可用资源，其绝对值表示等待使用该资源的进程个数。  

在刚开始，临界区没有进程，此时信号量为 m，每个进程进入临界区时，信号量减1，减到-(n-m）为止，即最多有 n - m 个进程等待使用该临界区。

所以，信号量 S 的值的变化范围是 [m - n, m] 。

5、动态分区的     循环适应算法     算法可以使内存中的空闲分区分布得更均匀。

解： 动态分配算法总结如下：

动态分配算法	空闲表排列	特点
最先适应算法（First-fit） （首次适应算法）	按地址递增	综合性能最好。算法开销小，回收分区后一般不需要对空闲分区队列重新排列。
最佳适应算法（Best-fit）	按容量递增	总能找到满足空间大小需要的最小空闲分区给作业。性能较差，产生最多的外部碎片。回收分区后可能需要对空闲分区队列重新排列。
循环适应算法（Next-fit） （邻近适应算法）	分配内存时从上次查找 结束的位置开始继续查找	能使内存中的空闲块分布更均匀，减少查找空闲块的开销。导致内存的末尾分配空间分裂成小碎片。
最坏适应算法（Worst-fit）	按容量递减	可减少难以利用的小碎片，但导致很快没有较大的内存块，性能很差，不利于大进程，算法开销大。

6、虚拟存储器具有    对换性    、   多次性    和虚拟性三大特征。

7、下列进程调度算法中，(   A   ) 可能会出现进程长期得不到调度的情况。

A. 静态优先权法                                            B. 抢占式调度中采用动态优先权法

C. 分时处理中的时间片轮转调度算法            D. 非抢占式调度中采用 FIFO 算法

解：  常用的进程调度算法有：先来先服务、短作业优先、优先级法（抢占式和非抢占式）、时间片轮转。（还有最短剩余时间优先法、多级队列法、多级反馈队列法、高响应比优先法）

A项，根据《操作系统原理》可知，静态优先级是在创建进程时就确定下来的，且在进程的整个运行期间保持不变。静态优先级调度算法易于实现，系统开销小，但其主要问题是会出现 “饥饿” 现象，即某些低优先级的进程无限期地等待 CPU。在负载很重的计算机系统中，若高优先级的进程很多，形成一个稳定的进程流，就使得低优先级进程永远也得不到 CPU 。

B项，抢占式优先级法：当前进程在运行进程中，一旦有另一个优先级更高的进程出现在就绪队列中，进程调度程序就停止当前进程的运行，强行将 CPU 分给那个进程。动态优先级是随着进程的推进而不断改变的，如果系统中等待 CPU 很长时间的进程可以逐渐提升其优先级。

C项，时间片轮转调度算法，选出就绪队列（先入先出排列）的队首进程，让它在 CPU 上运行一个时间片的时间。

D项，FIFO 算法，即每次调度从就绪队列中选择一个最先进入该队列的进程，把 CPU 分给它，令其投入运行。（有利于长作业（进程）、CPU 繁忙型作业）

8、磁盘的 I/O 控制主要采取(      C     ) 方式。

A. 程序 I/O                      B. 中断                       C. DMA                  D. SPOOLing

解：  在《操作系统原理》第六章的设备管理中，引入直接存储器存取方式，即 DMA，是为了避免磁盘 I/O 时 CPU 被中断的次数过多，降低 CPU 的工作效率，可能延误数据的接收，导致数据丢失的情况。

【拓展】

DMA 的传送基本思想：用硬件机构实现中断服务程序所要完成的功能。

DMA 方式具有以下四个特点：

（1）数据是在内存和设备之间直接传送的，传送过程中不需要 CPU 干预。

（2）仅在一个数据块传送结束后，DMA 控制器才向 CPU 发出中断请求。

（3）数据传送过程中，CPU 与外设并行工作，提高了系统效率。

（4）数据的传送控制工作完全由 DMA 控制器完成，速度快，适用于高速设备的数据结组传送。

可搭配链接学习：【考研复习】《操作系统原理》孟庆昌等编著课后习题+答案——第六章

9、 通道又称 I/O 处理机，它用于实现 (   内存与外设  )  之间的信息传输。

10、 下面叙述正确的是(     C     ) 。

A. 程序段是进程存在的唯一标志

B. 系统通过 PCB 来控制和管理进程，用户可以从 PCB 中读出与本身运行状态相关的信息

C. 当进程有执行状态变为就绪状态时，CPU现场信息必须被保存在PCB中

D. 当进程申请 CPU 得不到满足时，它将处于阻塞状态

解： A项，PCB 是进程存在的唯一标志。

B项，用户无法从 PCB 中读出与本身运行状态相关的信息，只能由操作系统读取。

D项，当进程申请 CPU 得不到满足时，它将处于就绪状态。

【拓展】

被中断的 CPU 现场信息包括所有的 CPU 寄存器(如通用寄存器、段寄存器等)，程序计数器（PC）和处理机状态字(PSW)的信息。

11、在没有快表的情况下，分页系统要访问(     B     )次内存。

A. 1             B. 2                C .3                D. 4

 解：在请求分页系统中，在没有快表的情况下，存取一个数据（或一条指令）至少要访问 2 次内存：一次是访问页表，确定存取对象的物理地址；另一次是根据这个物理地址存取数据（或指令）。

【拓展】

段页式存储管理方式中，如果没有引入快表，则每取一次数据，要访问（   3  ）次内存。 

解：在段页式系统中，在没有快表的情况下，需要一次访问段表，一次访问页表，一次取指令，即一共至少 3 次访问内存。

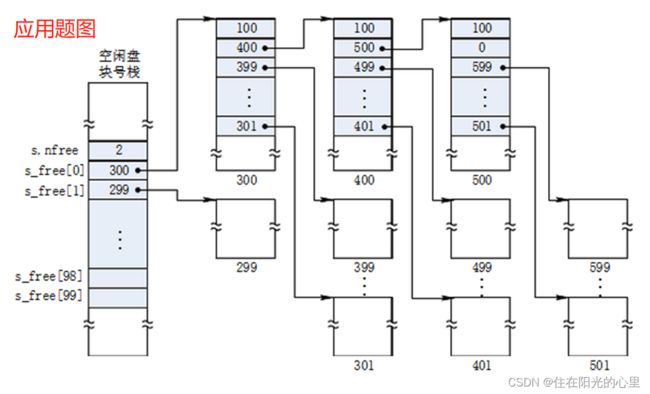
12、某类Unix系统采用成组链接法来管理磁盘的空闲空间，给出该系统的磁盘块分配及回收算法（流程图或描述）。

解：（1）分配算法：

先检查空闲盘块号栈是否上锁，如没有，便从栈顶取出一空闲盘块号，将与之对应的盘块分配给用户，然后将栈顶指针下移一格。

若该盘块号已是栈底，即 S. free(0)，到达当前栈中最后一个可供分配的盘块号。读取该盘块号所对应的盘块中的信息：即下一组可用的盘块号入栈。

原栈底盘块分配出去。修改栈中的空闲盘块数。

（2）回收算法：回收盘块号记入栈顶，空闲数 N 加 1，N 达到 100 时，若再回收一块，则将该 100 条信息填写入新回收块。

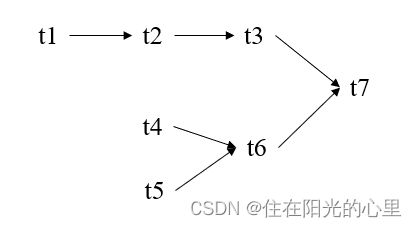
13、 分析下面给出的表达式的并行性，并用信号量机制实现该表达式的并行计算。（10分）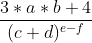                                                                         

解：设 ；；；

；；；

并行性分析如下:

 假设进程 ti 运行完成后释放的信号量为 si;

进程t1:
while(TRUE){
    wait(mutex);
    执行t1;
    signal(mutex);

    singal(s1);
}

进程t2:
while(TRUE){
    wait(s1);   //确保 t1 在 t2 之前

    wait(mutex) ;
    执行t2;
    signal(mutex);

    singal(s2);
}

进程t3:
while(TRUE){
    wait(s2);  //确保 t2 在 t3 之前

    wait(mutex) ;
    执行t3;
    signal(mutex);

    singal(s3);
}

进程t4:
while(TRUE){
    wait(mutex) ;
    执行t4;
    signal(mutex);

    singal(s4);
}

进程t5:
while(TRUE){
    wait(mutex) ; .
    执行t5;
    signal(mutex);

    singal(s5);
}

进程t6:
while(TRUE){
    wait(s4);    //确保 t4 在 t6 之前
    wait(s5);    //确保 t5 在 t6 之前

    wait(mutex) ;
    执行t6;
    signal(mutex);

    singal(s6);
}

进程t7:
while(TRUE){
    wait(s3);    //确保 t3 在 t7 之前
    wait(s6);    //确保 t6 在 t7 之前

    wait(mutex) ;
    执行t7;
    signal(mutex);

    singal(s7);
}

wait()：信号量非零时减一；

signal()：信号量非满时加一；