python数据分析完整流程-幸福感预测
一.数据背景及问题描述
- 数据来源:课题来源于天池大赛,数据来源于中国人民大学中国调查与数据中心《中国综合社会调查(CGSS)》项目,为多阶分层抽样的截面面访调查。
- 研究背景:在社会科学领域,幸福感的研究占有重要的位置。这个涉及了哲学、心理学、社会学、经济学等多方学科的话题复杂而有趣;同时与大家生活息息相关,每个人对幸福感都有自己的衡量标准。如果能发现影响幸福感的共性,生活中是不是将多一些乐趣;如果能找到影响幸福感的政策因素,便能优化资源配置来提升国民的幸福感。目前社会科学研究注重变量的可解释性和未来政策的落地,主要采用了线性回归和逻辑回归的方法,在收入、健康、职业、社交关系、休闲方式等经济人口因素;以及政府公共服务、宏观经济环境、税负等宏观因素上有了一系列的推测和发现。
- 研究目标:使用公开数据的问卷调查结果,选取其中多组变量,包括个体变量(性别、年龄、地域、职业、健康、婚姻与政治面貌等等)、家庭变量(父母、配偶、子女、家庭资本等等)、社会态度(公平、信用、公共服务等等),来预测其对幸福感的评价。
二.描述性统计
1. 数据介绍
1.1 标签介绍
数据集的标签是happiness变量,是一个取值为1到5的有序变量,表示幸福程度。数值越大表示幸福感越强,1表示感到非常不幸福,5表示非常幸福。
1.2 特征介绍
数据集中一共有139个特征,大致可以分为两类:第一类是与自身相关的,第二类是
与自身家庭相关的。第一类中与自身相关的可以大致细分为3个方面:第一方面是外在,比如出生日期、性别、身高、体重、身体健康状况等;第二方面是精神认知方面,比如是否有信仰宗教、社会公平度、对社会各项公共的满意程度等,第三方面主要是经济方面、比如过去现在以及将来所处社会等级、工作收入等。第二类是家庭基本信息,比如父母亲配偶的年龄、工作、政治面貌等。
2. 描述性统计
#查看数据的总体情况,可以看出共有140个变量,其中的happiness为标签变量
data.info(verbose=True,null_counts=True)
2.1 标签
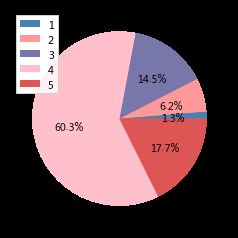
发现数据存在12个异常值,由于12占整体的数据量较少,此处描述性统计暂时不统计标签小于0的值,对结果影响不大,后续预处理将对标签进行处理 统计标签大于0 的分布从标签饼图可以看出觉得幸福的人最多,占样本的60.3%,其次是非常幸福的人,占样本的17.7%,感到非常不幸福的人较少仅占1.3%
label=data['happiness']
label.value_counts
colors=['steelblue','#ff9999','#7777aa','pink','#dd5555']
label_list=[]
label_c=[]
for i in range(1,6):
label_list.append(data.loc[label==i,'happiness'].count())
plt.pie(label_list,labels=[1,2,3,4,5],autopct='%.1f%%',colors=colors)
plt.legend()
#样本类型查看
data['survey_type'].value_counts()

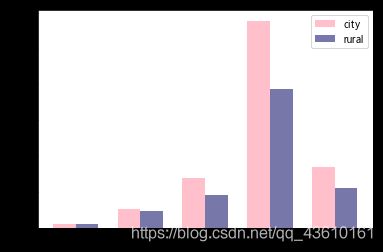
从样本类型的统计看出,城市中的样本占大多数。作出不同类别群体的幸福分布条形图,从图中可以看出两个群体关于幸福感的整体趋势是相同的,但城市类别中,感到特别幸福的人的比例略高于农村地区。
city=data[data['survey_type']==1]
rural=data[data['survey_type']==2]
city_list=[]
rural_list=[]
for i in range(1,6):
city_list.append(city.loc[city['happiness']==i,'happiness'].count())
rural_list.append(rural.loc[rural['happiness']==i,'happiness'].count())
width=0.35
plt.bar(range(1,6),city_list,width=width,label='city',color='pink')
plt.bar(np.arange(1,6)+width,rural_list,width=width,label='rural',color='#7777aa')
plt.xticks(np.arange(1,6)+0.1,[1,2,3,4,5])
plt.legend()
plt.show
**#性别**
sex_list=[]
for i in range(1,3):
sex_list.append(data.loc[data['gender']==i,'happiness'].count())
plt.pie(sex_list,colors=['#7777aa','pink'],labels=['F','M'],autopct='%.1f%%')
plt.legend()
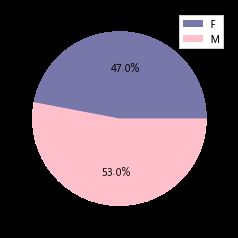
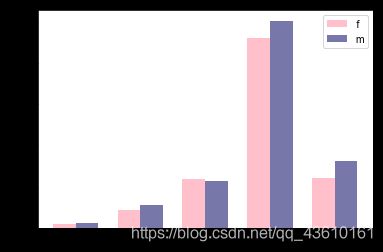
性别分布的饼图如上图所示,F代表男性,M代表女性,可以看出女性受访者略多于男性,再做出不同性别的幸福感分布条形图,可看出男女 的幸福感分布走势基本相同,再通过比较均值进一步进行研究,这两个类别幸福感均值的条形图如图,可以看出女性群体的幸福感均值略高于男性。
f=data.loc[data['gender']==1]
m=data[data['gender']==2]
f_list=[]
m_list=[]
for i in range(1,6):
f_list.append(f.loc[f['happiness']==i,'happiness'].count())
m_list.append(m.loc[m['happiness']==i,'happiness'].count())
width=0.35
plt.bar(range(1,6),f_list,width=width,label='f',color='pink')
plt.bar(np.arange(1,6)+width,m_list,width=width,label='m',color='#7777aa')
plt.xticks(np.arange(1,6)+0.1,[1,2,3,4,5])
plt.legend()
plt.show

#年龄
用出生日期减去调查日期得到受访者的年龄。年龄分布的盒形图如下,从该图可以看出,样本中年龄大的有90多岁,小的不到20岁,大多数受访者年龄为40-60岁。按照幸福程度分组,可以看出组别均值之间存在差异,感到非常幸福的人的年龄均值最大。
#年龄
data['survey_time']=pd.to_datetime(data['survey_time'])
data['survey_year']=data['survey_time'].dt.year
data['age']=data['survey_year']-data['birth']
plt.boxplot(data['age'],patch_artist='pink')


#身高
身高箱线图如图,身高最小值不到120cm、最大值超过190cm,有较多离群值。按照幸福感分组得到分组条形图,如图,幸福感为4即感到比较幸福的群体有较多离群值,同时也能看出 该群体的身高均值最大
plt.boxplot(data['height_cm'],patch_artist='pink')

#体重
体重的箱线图如图。可以看出有较多样本的体重最小的仅有40,有较多小的离群值。体重的单位是斤,考虑到受访者都是成年人,猜想这部分体重小的离群点可能是受访者混淆了单位,填的是以公斤计算的体重。在后续特征处理的时候考虑将体重乘以2。
plt.boxplot(data['weight_jin'],patch_artist='pink')

#身体健康
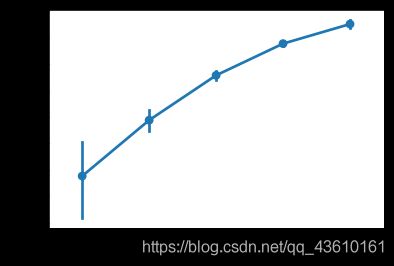
身体健康分布的饼图如下图,这是一个顺序变量,1代表很不健康,5代表很健康。可以看出比较健康的人最多,占38.8%,很不健康的人最少,占3.1%。右图反应的是健康各个等级的均值走势图,可以看出健康等级越高的群体,幸福感均值也越大。
health_list=[]
for i in range(1,6):
health_list.append(data.loc[data['health']==i,'happiness'].count())
plt.pie(health_list,labels=[1,2,3,4,5],autopct='%.1f%%')
plt.legend()
hp=[]
for i in range(1,6):
hp.append(data.loc[data['health']==i,'happiness'].mean())
plt.plot(range(1,6),hp,color='b',markersize=5,markeredgecolor='r',marker='o',label='health-happiness')
plt.title('不同健康情况的幸福感均值分布')
plt.xlabel('健康状况')
plt.ylabel('幸福等级')
plt.legend()
2.3精神认知层面
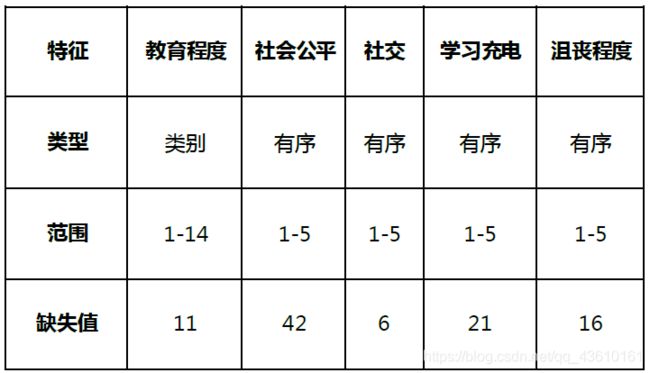
#教育程度
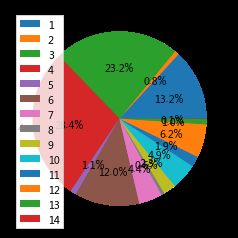
教育程度的饼图如图,图中数值的含义是:1=没有受过任何教育;2=私塾、扫盲班;3=小学;4=初中;5=职业高中;6=普通高中;7=中专;8=技校;9=成人大学专科;10=正规大学专科;11=成人大学本科;12=正规大学本科;13=研究生即以上;14=其他。从图中可以看出受访者中学历为初中的人最多,其次是小学,都不太高,可能是由于受访者大多数较年长,以前的教育资源较缺乏。右图是各个教育程度的幸福均值折线图,可以看出不同类别之间存在着明显的差异,教育程度为“其他”的幸福感最低,教育程度为2(小学)和13(研究生及以上)的两个群体幸福感较高。
edu=[]
for i in range(1,15):
edu.append(data.loc[data['edu']==i,'happiness'].count())
plt.pie(edu,labels=np.arange(1,15),autopct='%.1f%%')
plt.legend()
edu_=data[data['edu']>0]
sns.pointplot('edu','happiness',data=edu_)

#社会公平
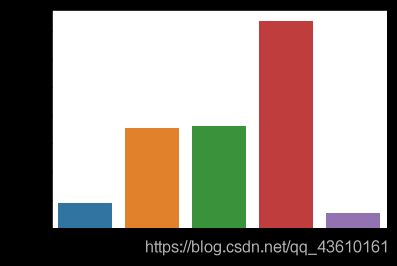
社会公平性是取值1-5的有序变量,数值越大表示越觉得公平,1表示认为社会完全不公平,5表示认为完全。从分布的条形图可以看出绝大多数的看法是4(认为社会较公平)。右图是不同看法群体的均值,可以看出认为社会越公平的群体,幸福感均值也越大。
equ=data[data['equity']>0]
sns.countplot('equity',data=equ)
sns.pointplot('equity','happiness',data=equ)
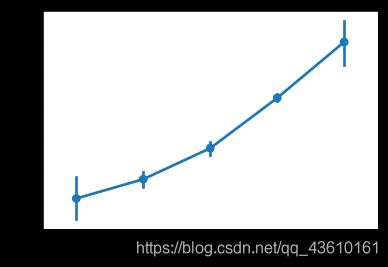
#社交
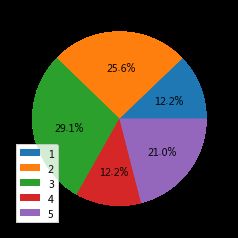
是取值为1-7的有序变量,取值越低,代表社交频率越频繁。从饼图可以看出,2(很少社交)的人最多,其次是3(有时社交)。条形图是不同社交程度群体的均值,可以看出社交频率高的群体相对于频次较低的群体幸福感均值高。
social=[]
for i in range(1,6):
social.append(data.loc[data['social_friend']==i,'happiness'].count())
plt.pie(social,labels=range(1,6),autopct='%.1f%%')
plt.legend()
lu=data[data['social_friend']>0]
sns.pointplot('social_friend','happiness',data=lu)

#学习充电
这是一个顺序变量,值越大表示课外充电频率越高。可以看出将近一半的人空闲时间从不学习,仅有2.4%的人课外学习频繁。右图是不同学习频率群体的均值,可以看出随着频率的增加,幸福感均值也增加,群体4(经常学习)和群体5(学习非常频繁)两个群体差异较小
learn=[]
for i in range(1,6):
learn.append(data.loc[data['learn']==i,'happiness'].count())
plt.pie(learn,labels=range(1,6),autopct='%.1f%%')
plt.legend()
plt.title('学习充电分布')
st=data[data['learn']>0]
sns.pointplot('learn','happiness',data=st)

#沮丧频繁程度
为取值1-4的顺序变量,值越小表示越频繁。可以看出大多人很少感到沮丧,仅有1.1%的人总是感到沮丧。从折线图可以得知沮丧程度越频繁的群体,幸福感均值也就越低。
de=[]
for i in range(1,6):
de.append(data.loc[data['depression']==i,'happiness'].count())
plt.pie(de,labels=range(1,6),autopct='%.1f%%')
plt.legend()
plt.title('沮丧程度分布')
det=data[data['depression']>0]
sns.pointplot('depression','happiness',data=det)
2.4.社会经济地位

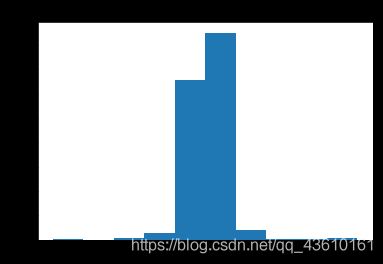
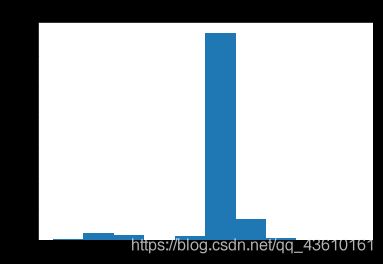
关于受访者主观认为其所处的社会地位的6个问题中,涉及到多个时间点的信息,以目前所处等级为基准,对其他3个变量进行相减做差并等频分组,可以得到数年来受访者所处等级的变化,可作为新的变量加入特征集,其分布直方图如左下图.
据统计,65.6%的受访者认为当前所处社会等级高于14岁时家庭所处的等级,56.4%的受访者认为当前所处的社会等级高于10年前,89.04%的受访者认为未来10年后的所处等级会不低于现在;
data['now-14']=data['class']-data['class_14']
data['now-class_10_before']=data['class']-data['class_10_before']
plt.hist(data['now-14'])
plt.title('与十四岁对照等级变化分布图')
data.loc[data['now-14']>0,'now-14'].count()/8000
plt.hist(data['now-class_10_before'])
plt.title('与十年前对照等级变化分布图')
data.loc[data['now-class_10_before']>0,'now-class_10_before'].count()/8000
data['now-class_10_after']=data['class_10_after']-data['class']
plt.hist(data['now-class_10_after'])
plt.title('与十年后对照等级变化分布图')
data.loc[data['now-class_10_after']>=0,'now-class_10_after'].count()/8000
2.4.家庭收入
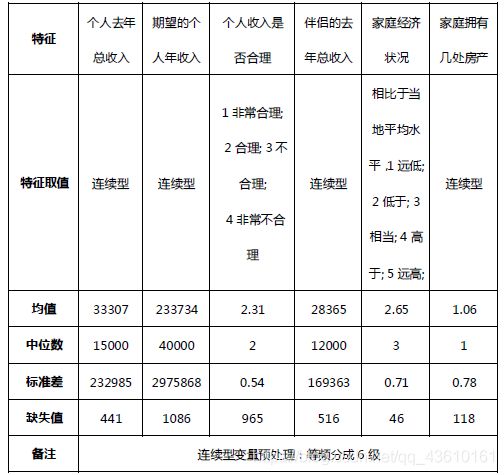
#收入
对收入进行分组,并统计不同组别对应得幸福感的不同,原始的收入数据分布具有大量极端值,右偏态显著,对其进行5组分组。可以看出,出去少于3000的收入人群,可能为退休老人,退役军官等,幸福感来源有所不同,其他人随着收入的增加,每组的幸福感均值也在增加,可见收入对幸福感有正向支撑作用。
def income_cut(income):
if income<=3000:
return 1
if 300035000:
return 5
data["income"]=data["income"].map(income_cut)
plt.hist(data['income'])
sns.pointplot('income','happiness',data=data)
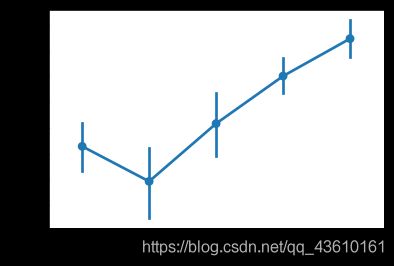
#房产拥有情况
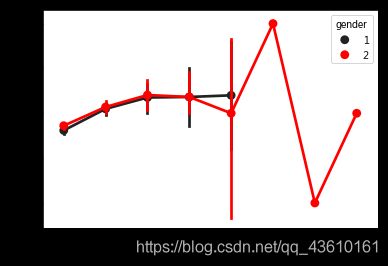
在拥有房产小于4套时,幸福感随着房产的增多而增加,之后再随房产数量在增多,幸福感反而发生了大的波动,进一步加入性别因素,探究不同性别对于房产的不同感知,可见男女在房产小于4时的幸福感趋势基本相同,相对来说,高数量房产的拥有者多为女性,推测为女强人类型或者为异常值。
data_list=data[data['house']<10]
data_1=data_list[data_list['house']>0]
sns.pointplot('house','happiness',data=data_1)
sns.pointplot('house','happiness',data=data_1,hue='gender',color='r')
三.数据预处理
3.1缺失值填补
#去除严重缺失值
data=data.drop(['edu_other','invest_other','join_party','property_other','s_work_status','s_work_type','work_manage','work_status','work_type','work_yr'],axis=1)
#data.info(verbose=True,null_counts=True)
数据缺失值填补-方法1,按照数据分布进行填补
均值填充----数据分布近似正态
中位数填充—数据存在离群点或者偏态分布
众数填充—数据为不分大小的标签值,如男女
data['edu_yr'].describe()
data.loc[data['edu_yr']<0,'edu_yr']=np.NAN
data['edu_yr'].value_counts()
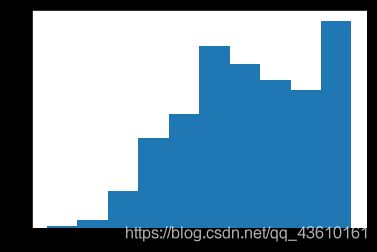
plt.hist(data['edu_yr'].dropna())
#发现被调查者取得毕业证年份呈明显的右偏分布,因此可以取中位数进行缺失值填补
data['edu_yr']=data['edu_yr'].fillna(data['edu_yr'].median())
data['edu_status']=data['edu_status'].fillna(data['edu_status'].median())
缺失值处理–方法2
插值法填充,使用缺失值前一个和后一个的平均数
data['social_neighbor'] = data['social_neighbor'].interpolate()
data['social_friend'] = data['social_friend'].interpolate()
缺失值处理-方法3
随机森林填充 随机森林,指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出。简单来说,是一种bagging的思想,采用bootstrap,生成多棵树,CART(Classification And Regression Tree)构成的。对于每棵树,它们使用的训练集是从总的训练集中有放回采样出来的,这意味着,总的训练集中的有些样本可能多次出现在一棵树的训练集中,也可能从未出现在一棵树的训练集中。对于一个有n行的数据集,out of bag 的概率大概是1/e=1/3。n趋向无穷大的时候,(1-1/n)^n~1/e。
理解上这个1/n是每次抽样的比率吗?所以out of bag到底是什么意思?
1.在与其它现有的算法相比,其预测准确率很好 2.在较大的数据集上计算速度依然很快 3.不需要降维,算法本身是采取随机降维的 4.他能处理有缺失值的数据集。算法内部有补缺失值的函数 5.能给出变量的重要性 6.能处理imbalanced data set 7.能给出观测实例间的相似度矩阵,其实就是proximity啦,继而能做clustering 和 location outlier 8.能对unlabeled data 进行无监督的学习,进行clustering 9.生成的森林可以保留,应用在新的数据集上
#目前的缺失列"hukou_loc","family_income","minor_child","marital_1st","s_birth","marital_now","s_edu","s_political","s_hukou","s_income","s_work_exper"
list=["hukou_loc","family_income","minor_child","marital_1st","s_birth","marital_now","s_edu","s_political","s_hukou","s_income","s_work_exper"]
from sklearn.ensemble import RandomForestClassifier
for i in list:
re=data[data[i].notnull()]
rn=data[data[i].isnull()]
re_x=re[["province","gender","religion","edu","political","floor_area","health","hukou","son","daughter","status_peer","public_service_1"]].astype(float)
re_y=re[i].astype(float)
rn_x=rn[["province","gender","religion","edu","political","floor_area","health","hukou","son","daughter","status_peer","public_service_1"]].astype(float)
model=RandomForestClassifier()
model.fit(re_x,re_y)
pr=model.predict(rn_x)
data.loc[data[i].isnull(),i]=pr
3.2.异常值处理
#异常值处理
index_abnormal_weight = data.loc[data.weight_jin<70].index
for i in index_abnormal_weight :
if data["gender"].iloc[i]==1:
data["weight_jin"].iloc[i]=data["weight_jin"].iloc[i]*2
if data["gender"].iloc[i]==2:
if (data["height_cm"].iloc[i]>140) or (data["health"].iloc[i]>2):
data["weight_jin"].iloc[i]=data["weight_jin"].iloc[i]*2
data["weight_jin"].describe()
data.loc[data['income']<0,'income']=0
3.3.离散化处理
#离散化处理
#income
def income_cut(income):
if income<=3000:
return 1
if 300035000:
return 5
data["income"]=data["income"].map(income_cut)
data["s_income"]=data["s_income"].map(income_cut)
data["family_income"]=data["family_income"].map(income_cut)
data["inc_exp"]=data["inc_exp"].map(income_cut)
#处理时间特征
data['survey_time']=pd.to_datetime(data['survey_time'])
data['survey_year']=data['survey_time'].dt.year
#问卷年龄
data['age']=data['survey_year']-data['birth']
data['age'].describe()
def age_cut(birth):
if birth<=18:
return 1
if 1860:
return 5
data['age']=data['age'].map(age_cut)
#出生年代
data['birth'].describe()
def birth_cut(birth):
if birth<=1940:
return 1
if 19401985:
return 5
data['birth']=data['birth'].map(birth_cut)
data['edu_yr']=data['edu_yr'].map(birth_cut)
data["s_birth"]=data["s_birth"].map(birth_cut)
data["s_birth"]=data["s_birth"].map(birth_cut)
data["marital_1st"]=data["marital_1st"].map(birth_cut)
data["marital_now"]=data["marital_now"].map(birth_cut)
#房屋面积分组
def floor(x):
if 0<=x<=50:
return 1
elif 50400:
return 5
data["floor_area"]=data["floor_area"].map(floor)
#身高分组
def height(x):
if x<=130:
return 1
elif 130190:
return 5
data["height_cm"]=data["height_cm"].map(height)
#体重分组
def weight(x):
if x<=70:
return 1
elif 70150:
return 5
data["weight_jin"]=data["weight_jin"].map(weight)
#社会公共服务分组
def service(x):
if x<10:
return 0
elif 10<=x<30:
return 1
elif 30 3.4.独热编码
需要进行独热编码的有宗教,性别,省份,政治身份,户口,户口所在地等
from sklearn.preprocessing import OneHotEncoder
category_name=["survey_type","gender","religion","nationality","political",
"hukou","hukou_loc","province"]
category_feature=data[category_name]
category_feature
enc=OneHotEncoder(categories="auto")
category_feature=enc.fit_transform(category_feature).toarray()
category_feature=pd.DataFrame(category_feature)
data=pd.concat([data,category_feature],axis=1)
data.drop(category_name,axis=1)
3.5.特征选择
特征选择 模型在预处理后仍有176个变量,因此我们使用随机森林对特征进行选取,并对特征的重要性进行排序 可以看出对幸福感影响最大的前十个变量分别是社会地位,户口所在地,房产拥有,健康状况,沮丧程度等
用有抽样放回的方法(bootstrap)从样本集中选取n个样本作为一个训练集,用抽样得到的样本集生成一棵决策树。在生成的每一个结点:随机不重复地选择d个特征,利用这d个特征分别对样本集进行划分,找到最佳的划分特征(可用基尼系数、增益率或者信息增益判别)。重复步骤1到步骤2共k次,k即为随机森林中决策树的个数。用训练得到的随机森林对测试样本进行预测,并用票选法决定预测的结果。 用随机森林进行特征重要性评估的思想就是看看每个特征在随机森林中的每颗树上做了多大的贡献,然后取平均值,最后比较特征之间的贡献大小。
data=pd.DataFrame(data)
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
import matplotlib.pyplot as plt
import numpy as np
from plotly.graph_objs import *
from plotly.offline import init_notebook_mode, iplot
#定义一个由500颗决策树组成的随机森林模型
rf_model = RandomForestClassifier(n_estimators=500,max_depth=5,random_state=0,n_jobs=-1)
#训练
rf_model.fit(data,y)
#获取特征的重要性
importances = rf_model.feature_importances_
#对特征的重要性进行排序
indices = np.argsort(importances)[::-1]
cols_name = data.columns[1:]
for f in range(10):
print("%2d) %-*s %f" % (f + 1,30,cols_name[indices[f]],importances[indices[f]]))
plt.figure(figsize=(10, 8))
plt.title("特征的重要性")
plt.bar(range(data.shape[1]),importances[indices],color="lightblue",align="center")
plt.xticks(range(data.shape[1]),cols_name)
plt.xlim([-1,data.shape[1]])
plt.show()
model = SelectFromModel(rf_model, prefit=True)
data= model.transform(data)
data.shape
四.模型建立
#模型拟合
#进行k折交叉验证下的xgboost回归
from sklearn.metrics import accuracy_score
from xgboost.sklearn import XGBRegressor
from sklearn.metrics import mean_squared_error
from sklearn.externals import joblib
from sklearn.model_selection import KFold
from sklearn.metrics import roc_curve,roc_auc_score,confusion_matrix
data=pd.DataFrame(data)
kfold = KFold(n_splits=10, shuffle = True, random_state= 11)
model = XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=0.1,
colsample_bytree=0.971, gamma=0.11, learning_rate=0.069, max_delta_step=0,
max_depth=4, min_child_weight=1, missing=None, n_estimators=300,
n_jobs=-1, nthread=50, objective='reg:linear', random_state=0,
reg_alpha=0.1, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=True, subsample=1.0)
mse = []
auc=[]
i = 0
for train, test in kfold.split(data):
x_train = data.iloc[train]
y_train = y.iloc[train]
x_test = data.iloc[test]
y_test = y.iloc[test]
model.fit(x_train,y_train)
y_pred = model.predict(x_test)
y_test= pd.DataFrame(y_test)
xg_mse = mean_squared_error(y_true=y_test,y_pred=y_pred)
predictions = [round(value) for value in y_pred]
accuracy = accuracy_score(y_test, predictions)
mse.append(xg_mse)
auc.append(accuracy)
print("mean squared_error",xg_mse)
print("accuracy",accuracy)
joblib.dump(filename="xg"+str(i),value=model)
i+=1
print("xgboost-mean squared_error",np.mean(mse))
五.结果分析
对于幸福感的预测,我们尝试多次后发现准确率很难再进行提升,可能原因有:
个人对于幸福感的定义不同。因此,结合自身条件对自己的幸福感级别做定义,作为我们的预测标签,这本身就处于不同的标准之上,即两个不同的人,都对自己的幸福感评级为3级,但3级对于有些人而言算比较幸福,对有些人而言并不能算得上比较幸福,因此这种个别差异导致幸福感很难用相同的标准去预测每个人。
其次,影响不同人的幸福感因素不同,也有可能有些影响人幸福感的因素并未纳入调查变量中,导致预测精度较低。
存在更加适合预测的模型或者模型的参数有待进一步调优。