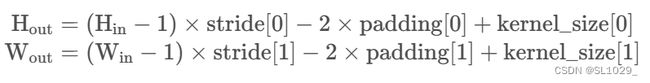深度解析转置卷积，理解转置卷积的原理

参考文章：

转置卷积（Transposed Convolution）_太阳花的小绿豆的博客-CSDN博客_转置卷积

抽丝剥茧，带你理解转置卷积（反卷积）_史丹利复合田的博客-CSDN博客_逆卷积和转置卷积

参考视频：

转置卷积（transposed convolution）_哔哩哔哩_bilibili

转置卷积

转置卷积（Transposed Convolution） 在语义分割或者对抗神经网络（GAN）中比较常见，其主要作用就是做上采样（UpSampling）。在有些地方转置卷积又被称作fractionally-strided convolution或者deconvolution，但deconvolution具有误导性，不建议使用。对于转置卷积需要注意的是：

• 转置卷积不是卷积的逆运算
• 转置卷积也是卷积

 普通卷积

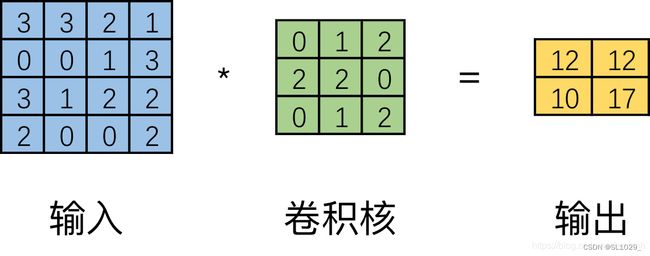
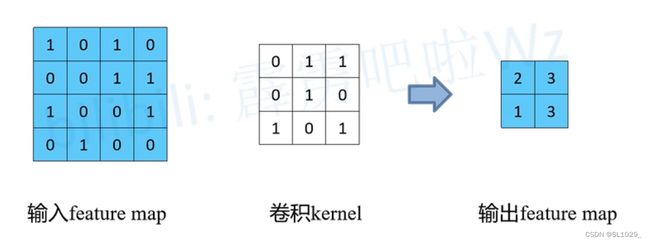
为了了解转置卷积，我们先来看普通卷积：

如上图普通卷积核一步一步滑动窗口得到特征输出，但实际上在计算机中并不会如上图所示计算（这样计算效率比较低），计算机会将卷积核转换成等效的矩阵，将输入转换为向量。通过输入向量和卷积核矩阵的相乘获得输出向量。输出的向量经过整形便可得到我们的二维输出特征。具体的操作如下图所示。

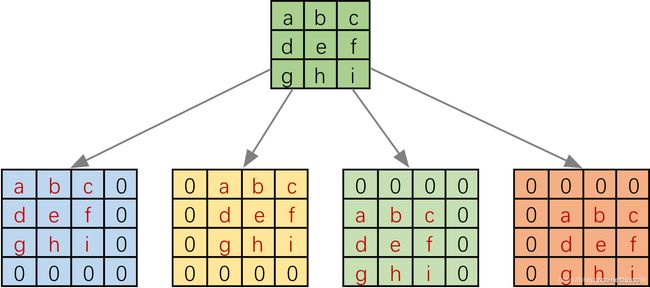
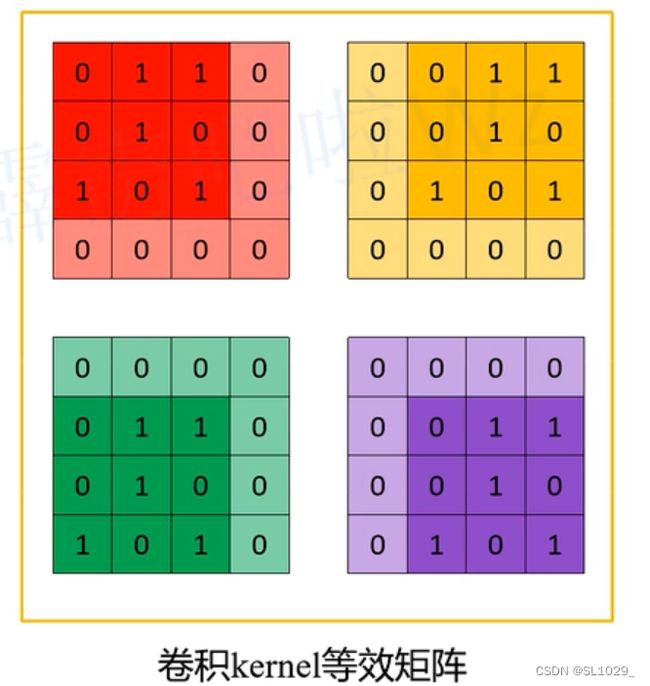
由于上图3x3卷积核要在输入上不同的位置卷积4次，所以通过补零的方法将卷积核分别置于一个4x4矩阵的四个角落。这样输入可以直接和这四个4x4的矩阵进行卷积，构成等效矩阵，而舍去了滑动这一操作步骤。

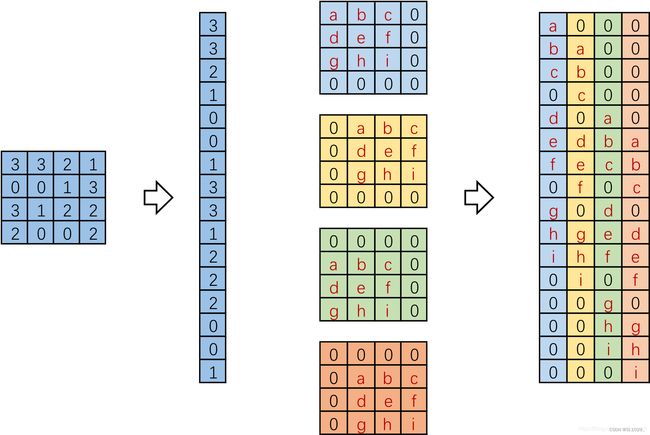
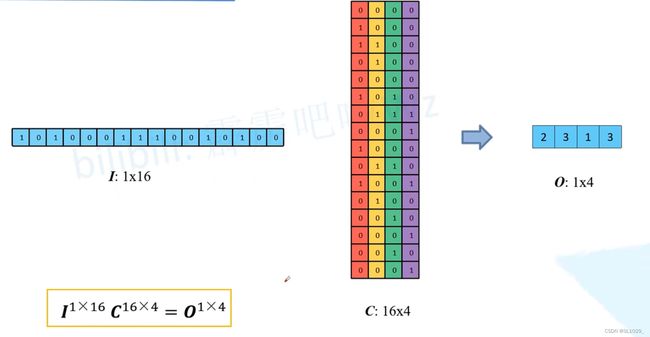
进一步的，将输入拉成长向量，四个4x4卷积核也拉成长向量并进行拼接，如下图。

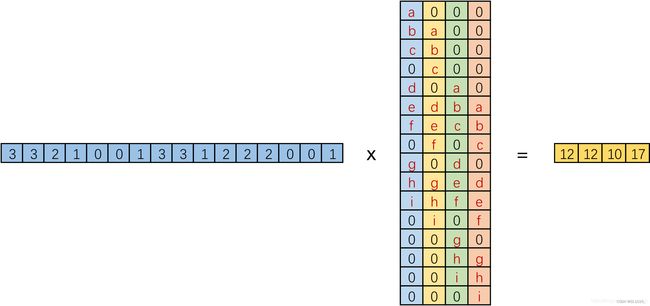
记向量化的图像为 I  ,向量化的卷积矩阵为C , 输出特征向量为 O ，则有：

∗=

将一个1x16的行向量乘以16x4的矩阵，得到了1x4的行向量。反过来将一个1x4的向量乘以一个4x16的矩阵是不是就能得到一个1x16的行向量呢？这就是转置卷积的思想

 

转置卷积

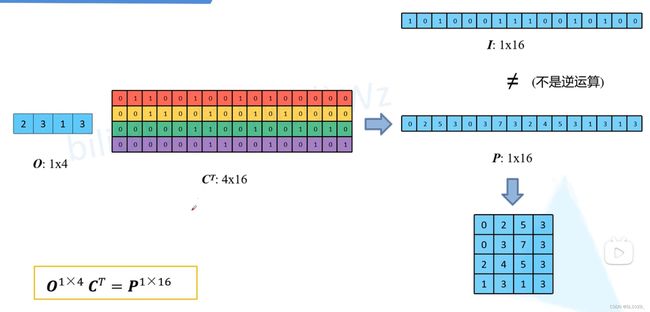
对应上面公式，我们有转置卷积的公式：

∗=

但这样操作只能输出原始的形状，并不能恢复到原始的数值，这里的P很明显和I不同（原因是这两个公式并不是可逆运算）但也因此称为转置卷积,实际卷积矩阵也不是上图中的C，这里只是转置卷积名字的由来。

那到底如何怎样才能得到转置卷积？

同样我们可以模仿上面构造等效矩阵，为了更好明白，我们举例来说明：

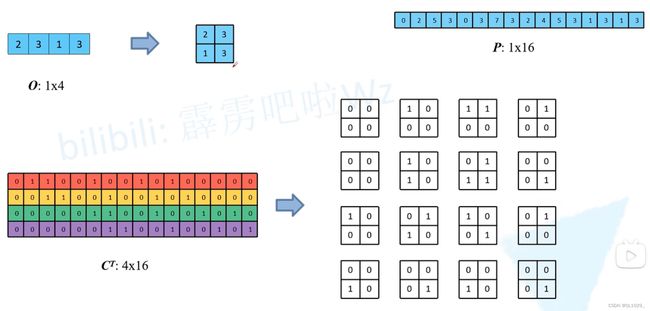
对于输入特征矩阵I作为输入特征，3*3的卷积对其进行普通卷积得到输出特征图O，构造等效矩阵

将I转变为1行16的矩阵，而卷积等效矩阵的每一个矩阵转化为一个16行1列的向量，再合并为16行4列的矩阵，做乘积就等效与原来的卷积运算，如下图，与上面写的的理论一样

此时与上面写的一样，我们不要求从O来得到I,我们只要求得到与I相同形状的P，可以看到将O与C的转置确实没有得到I,而是得到了P

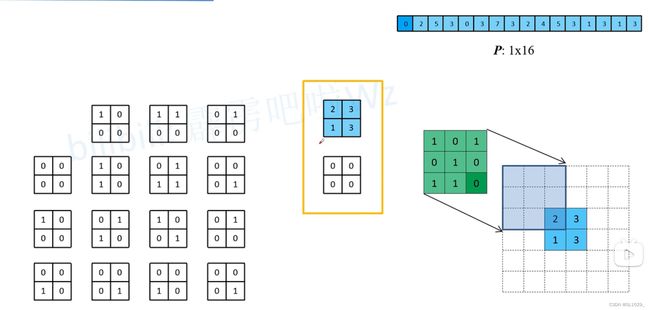
此时我们将O重新恢复到两行两列的矩阵，同时将C的转置的每一列恢复为两行两列的矩阵，一共有16个

我们将每一个O与16个2行2列的矩阵相乘可以得到图中的P,这时我们会发现一个有趣的现象：如下图第一个矩阵[0,0,0,0]与O相乘等于0，会等于图中绿色矩阵（实际上就是转置矩阵，但我们先不用管绿色矩阵怎么来的）与途中蓝色框相乘的值（空白格里面是0），第二个矩阵[1,0,0,0]与O相乘得到2,这会等于绿色矩阵与蓝色框向右一格的框相乘的值，以此类推会发现绿色矩阵（其实就是转置卷积）相当于对O矩阵周围填充2行2列得到的矩阵（也即整个虚线框矩阵）做普通卷积得到P。而P同时也是O矩阵与C矩阵的乘积。这样事实上绿色矩阵就是事实上的转置卷积

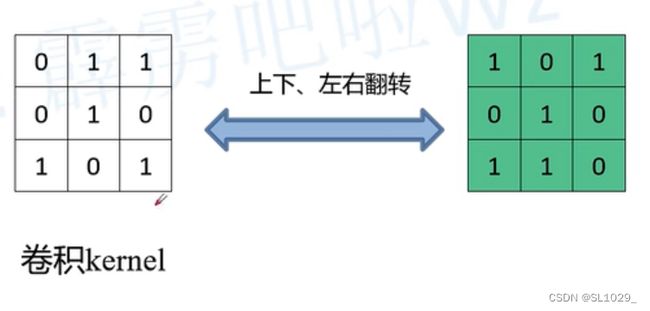
我们这时再来观察绿色矩阵，可以发现它会为原来的卷积上下左右翻转得到，如下图

因为这个绿色卷积矩阵对做了填充变化的O矩阵做卷积得到的结果，与转置矩阵C对没有填充的O矩阵做矩阵乘法结果相同，所以绿色矩阵称为转置卷积矩阵，操作称为转置卷积。

转置卷积操作步骤

下面是一般转置卷积操作步骤：

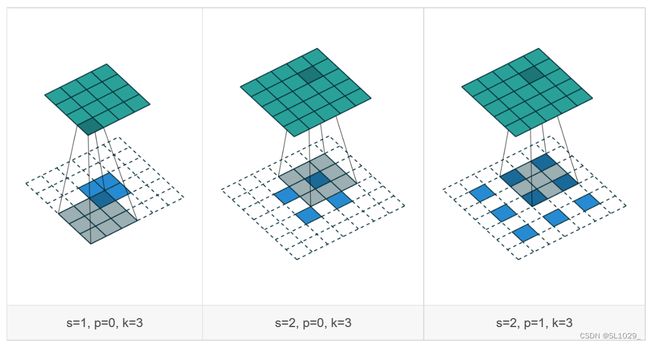
1.在输入特征图元素间填充s-1行、列0（其中s表示转置卷积的步距）

2.在输入特征图四周填充k-p-1行、列0（其中k表示转置卷积的kernel_size大小，p为转置卷积的padding，注意这里的padding和卷积操作中有些不同）

3.将卷积核参数上下、左右翻转

4.做正常卷积运算（填充0，步距1）

下图为转置卷积不同s、p的卷积过程示意图

转置卷积操作后特征图的大小可以通过如下公式计算：

总结：

1.转置卷积也是卷积

2.转置卷积不是卷积的逆运算

3.转置卷积的作用是为了上采样