常见的卷积、卷积变体以及其Pytroch实现

一、前言

近期读论文时发现不少论文使用的卷积不局限于常见的2D卷积，有轻量化的深度可分离卷积、改变通道数目的1*1卷积等，还有不少作者自定义的卷积网络。为了方便后期阅读论文，在此总结一下常见的卷积以及其Pytroch实现。这篇文章是建立在以及了解常见的2D卷积的基础上进行的。

二、常见的卷积以及其Pytroch实现

1. 2D卷积

注 现阶段在CNN中常见的卷积核大小都是长宽相等的，但2D卷积核卷积核大小并不一定要长宽相等。希望大家提前认识到这一点。

2D卷积网络是常用的卷积，卷积核的通道和输入图像/特征的通道一一对应进行卷积，得到的结果进行相加。拿【DL笔记6】从此明白了卷积神经网络（CNN）博客中的图片举个例子。

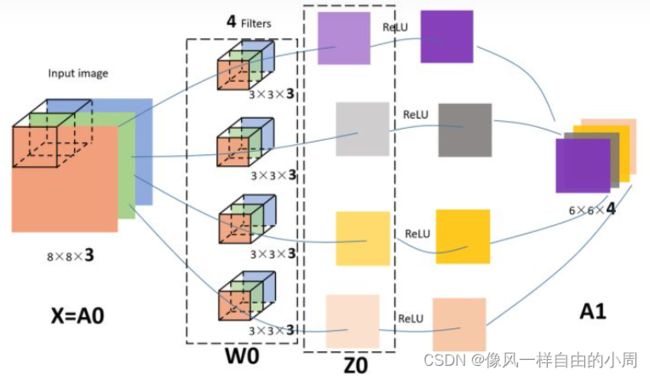
输入图像/特征通道数为3，尺寸为（8,8）；单个卷积核通道数要和输入通道数保持一致为3，尺寸为（3,3），步长为1，没有padding。2D卷积操作为卷积核橙红色通道对输入橙红色通道进行卷积操作，绿色对绿色进行卷积操作，蓝色对蓝色进行卷积操作，这样便得到了3个特征图结果，将得到的结果进行相加便得到了最终卷积核提取到的卷积特征。图中一共有4个卷积核故通过卷积核得到的特征有4个，concentrate在一起之后便得到了一个4通道的特征。其尺寸大小通过下面公式计算得到为通道数为4（和卷积核数量一样），尺寸大小为（6,6）。

N = (W − F + 2P )/S+1 # 除不尽的结果都向上取整。

简单的说了一下2D卷积的操作过程，现在我们来看一下如何用Pytroch实现2D卷积。Pytroch中实现2D卷积用的是Conv2d函数。首先，看一下该函数的参数默认值。一起一直用conv2d完成2D卷积，没太关注其它相关参数，误以为这个函数只能进行简单的2D卷积。

使用Conv2d实现2D卷积我们只要调整in_channels, out_channels, kernel_size, stride, padding, bias即可。其它的参数groups=1，如果设为其它的操作可能就不是2D卷积操作了，比如接下来要讲到的深度可分离卷积网络就是调整的groups参数，dilation=1，这是下面反卷积或者其它卷积要用到的。

• in_channels: 输入图片/特征的通道数，比如RGB就是三通道的。
• out_channels: 输出特征的通道数，和卷积核个数相等。
• kernel_size: 卷积核大小，常见的有3X3卷积核。可以为单独的一个数3，也可以是一个表示长宽的元组（3， 3）。卷积核并不一定长宽一样。
• stride: 步长。
• padding:填充数，用来弥补常见的卷积核对于边缘部分提取特征能力较差。
• padding_mode: 扩边的方式

# With square kernels and equal stride
m = nn.Conv2d(16, 33, 3, stride=2)
# non-square kernels and unequal stride and with padding
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
input = torch.randn(20, 16, 50, 100)
output = m(input)

其它参数在接下来不是默认值时再进行说明。

2. 3D卷积

3D卷积不太常见，不少很了解，后期了解再进行补充。

3. 1*1卷积

1* 1卷积，顾名思义就是卷积核大小为1*1的2D卷积，为啥要单独提出来呢，因为这东西挺常见的，下面要说到的深度可分离卷积也用到了这个。为什么常见呢？
网上找到的原因有以下几种

• 可以用1*1卷积层来代替全连接层。
  为啥可以替代？我在网上找了半天解答，发现有好几种观点，没有一个能彻底使我信服，故等下次遇到合理的解释时再次更新。
• 改变输入特征/图像的通道数，因为通过卷积后得到的特征通道数由2D卷积的卷积核个数决定。
• 1*1的卷积核计算起来运算量较小且参数量较少。这样在模型进行轻量化时就可以减少参数量。

和2D卷积一样，Pytroch代码只不过限定了kernel_size=1

# With square kernels and equal stride
m = nn.Conv2d(16, 33, 1, stride=2)
input = torch.randn(20, 16, 50, 100)
output = m(input)

4. 空间可分离卷积

高斯滤波器，大家或多或少有过了解，高斯滤波器有一个可分离性质可以用来降低计算量。高斯滤波器可以看作参数不改变的卷积，即高斯滤波器是空间可分离卷积的一种。有了高斯滤波器作为铺垫大家应该都知道空间可分离卷积是个啥东西了。下面详细说一下。
有些矩阵可以分解为向量和向量转置的乘积。举个栗子。

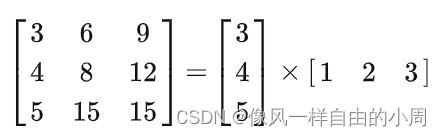
卷积核也是一个矩阵，有些卷积核可以分解为向量，那么这个性质有啥用呢，可以将卷积计算进行拆分，如下：

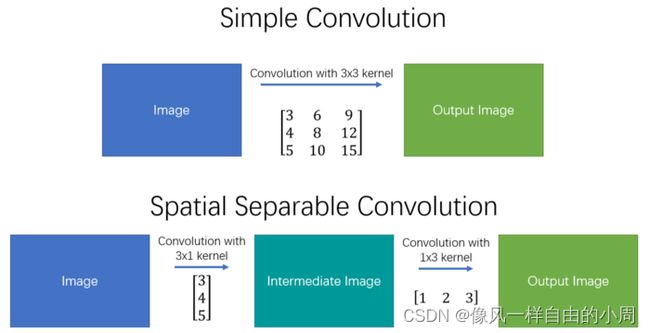
这样做有啥子好处呢，降低计算量。
首先我们要知道单个卷积核的计算量如何进行计算：卷积网络参数量和计算（FLOPs）的计算公式及代码（乘以2是因为卷积计算不止乘法还有一个加法）

现在我们进行一个简单的计算看一下计算量是否降低了。
分离前的FLOPs为 2X$k_h$X$k_w$X$C_i$X$C_o$XHXW.
分离后的FLOPs为 2X（$k_h$+$k_w$）X$C_i$X$C_o$XHXW
故在绝大部分的情况下采用分离计算可以大幅度降低计算量，将卷积进行空间分解可以进行模型轻量化。但有一个问题就是该卷积核能否进行分解，同时分解算法是啥？上述的计算过程是没有考虑分解算法的FLOPs的。

因此，空间可分离卷积有一定的局限性。

至于Pytroch的实现，有点困难，难点在于如何进行分解？是直接让神经网络去学习分解吗，即用两个卷积核大小为（k，1），（1，k）的卷积核来代替（k，k）的卷积核吗。那这个代码熟悉就两个2D卷积层，过于简单了，这里就不再展示了。

综上，空间可分离卷积的作用主要是用来降低计算量的。

5. 深度可分离卷积

深度可分离卷积核空间可分离卷积一样，都是用来进行降低计算量的，但二者的方法对象不一样，上述的空间可分离卷积分离对象是每一个通道层的空间特征，深度可分离卷积顾名思义分离对象就是通道数。那么咋分离呢？我们首先要知道2D卷积的输入通道数和卷积核通道数是一样的且在计算时一一对应，在求完卷积后有一个相加的操作，这个操作便会是的输入的每个通道上的数值进行了相加。如果不进行相加呢，即原来是3通道的输入，卷积核也是3通道的，通过卷积核后得到的特征应该是单通道的，如果不相加的话，输出特征通道数就是3通道的了。这样原来需要3个卷积核才能获得的结果只要1个卷积核就能办到了。当然这样可能会导致性能下降。用一下深度可分离卷积的图。

深度可分离卷积分为两部分：逐通道卷积、逐点卷积。

逐通道卷积操作过程如下。

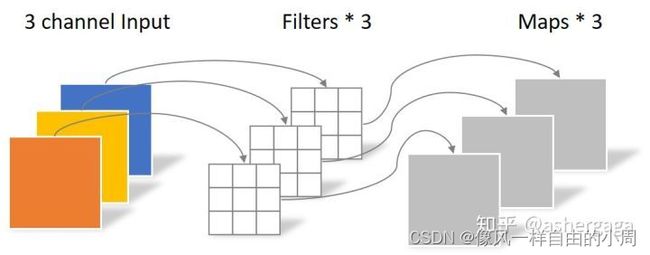
逐点卷积操作过程如下：

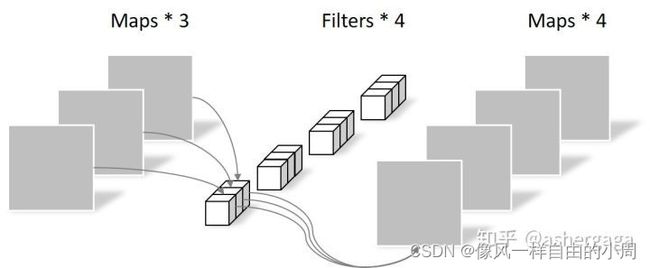
这里的逐点卷积用的就是2D卷积中的11卷积，操作和2D卷积操作一样。为啥要加这一个呢。一方面，卷积核的输出通道数应该是可以随意变化的，用11卷积便可以用较少的计算量实现这一点，通过逐通道卷积计算的输出通道数是固定的和输入图像/特征的通道数一样，这样便缺少了灵活性；另一方面，如果只通过逐通道卷积会导致输入的通道特征无法得到充分利用，这不是很可惜吗？

好了，通过这样做，计算量会降低吗。其实不用算因为逐点计算的FLOPs为2X1X$C_i$X$C_o$XHXW，逐通道计算在大部分情况下的计算量一定是小于2X（$k_h$+$k_w$-1）X$C_i$X$C_o$XHXW.故可以降低FLOPs，同时模型参数量也降低了。

Pytroch实现难点在于逐通道卷积，逐点卷积就是简单的1*1卷积。好在Pytroch只要调整一下groups这个参数就可以实现逐通道卷积了。以下为对groups这个参数的文档介绍。

• groups

是不是还是难以理解这个参数是啥意思？我也是，没关系，了解了接下来的分组卷积我们就会知道这个参数的妙用，现阶段我们只要知道，令gruops=in_channels就可以实现逐通道卷积就行了。

# 原卷积
m = nn.Conv2d(inplane, 33, 3)
# 深度可分离卷积
m1 = nn.Conv2d(inplane, inplane, 3, groups=inplane)
m2 = nn.Conv2d(inplane, 33, 1)

6. 分组卷积

分组卷积（Group Convolution）最早出现在AlexNet中。受限于当时的硬件资源，在AlexNet网络训练时，难以把整个网络全部放在一个GPU中进行训练，因此，作者将卷积运算分给多个GPU分别进行计算，最终把多个GPU的结果进行融合。因此分组卷积的概念应运而生。 深度可分离卷积中用到的逐通道卷积就是分组卷积的一种特殊形式。

分组卷积的思想是把输入图像/特征进行分组，针对每一个分组分别进行2D卷积，将得到的特征依次进行拼接得到最终特征。对输入图像/特征进行分组是对深度进行分组，比如分组数为groups，$C_i$便被平均分为gropus组，每组的通道数为$C_i/gropus$，因为对于2D卷积而言，卷积核通道数要和输入通道数一样，故对于每个小组里面的卷积核的通道数也要从原来的$C_i$变成$C_i/groups$。此外，因为卷积核的数量决定了输出特征的通道数，原来的输出特征的通道数为$C_{o}ut$，为了使得通过分组卷积后得到的特征依旧为$C_{o}ut$，这就要求对于每一个分组内的卷积核个数从$C_{o}ut$变成$C_{o}ut/groups$。这样就使得卷积核个数还和原来保持不变，但是卷积核通道数变少。这样便使得参数量和FLOPs变少。

借用一下这篇博客的图分组卷积（Group Convolution）
来说明一下可视化分组卷积的做法。


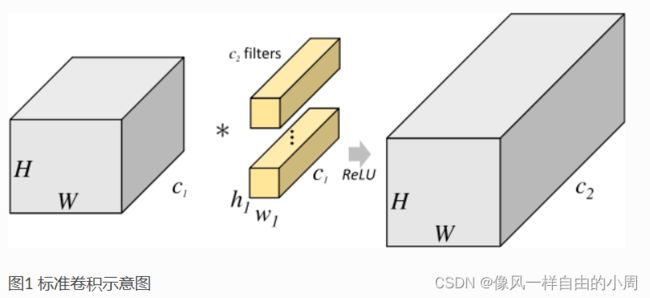
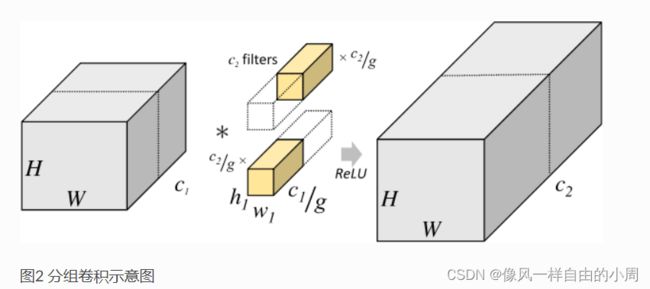
好了上面介绍了这么多，相信大家应该都明白了Pytroch中的Conv2d的参数groups的意义。如果要实现分组卷积，只要改变groups参数即可。

# 原卷积
m = nn.Conv2d(inplane, 33, 3)
# 分组卷积
m = nn.Conv2d(inplane, 33, 3, groups=2)

综上，分组卷积有助于进行并行计算，此外降低模型复杂度。

7.扩展卷积

扩展娟姐又叫空洞卷积，该结构出自论文MULTI-SCALE CONTEXT AGGREGATION BY DILATED CONVOLUTIONS（小声bb，有空了细读一下这篇论文再写一篇博客）。扩展卷积提出的目的是为了提高感受野。啥子叫感受野呢？

举一个有意思的例子，秦始皇的中央集权制，这个东西大家应该都很熟悉，有一天秦始皇想要绘制全国地图，咋办，下发命令，一级一级往下传，传到底层时，底层官吏执行命令，进行张量所辖区域，绘制所辖区域地图，然后再一级一级上报，一级一级汇总，这样上传到秦始皇这，秦始皇只要把几个省的地图一拼就得到了全国的地图。易知，底层官吏只能知道自己所辖区域的地图，所辖区域外的地图就不知道了，可能会导致盲人摸象的情况出现，绘制长江只能画出一个分支，不能绘制长江的地图，而秦始皇有全国地图就知道长江有多长了。这就是因为秦始皇有着更大的感受野。类别到图像，把绘制地图看作边缘检测这个任务，为了提高边缘检测的性能，就需要更大的感受野。（纯属个人胡思乱想）

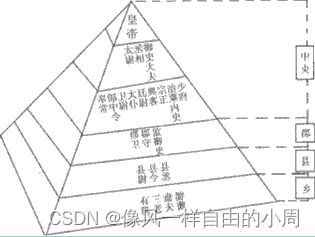
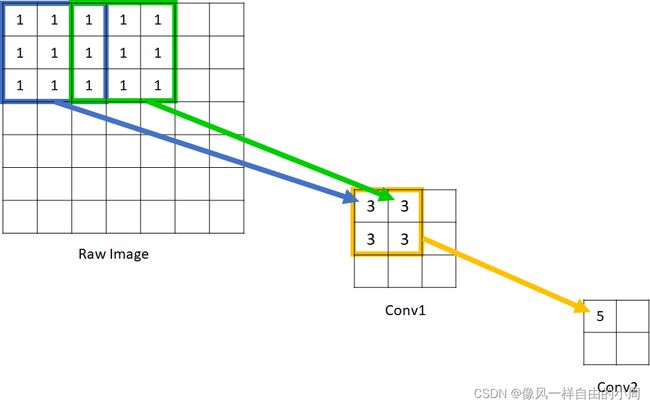
盗用一下网图深度神经网络中的感受野(Receptive Field)，下图中对于Conv1中的3而言，它的感受野就是蓝色或者绿色框所圈定的范围。

关于感受野的计算公式这里不再展示，有需要的小伙伴谷歌一下。

那么对于一个固定的卷积核如何扩大感受野呢。除了扩大卷积核的尺寸大小，有一个简单的方法就是上图中Conv1中的第一个3的感受野是Raw Image中蓝色框，我们把蓝色框扩大不就行了，做法比较粗暴，因为卷积中的点积计算是一一对应的，虽然你扩大了蓝色框，但点积只能计算蓝色框中的9个点，故需要跳过某些点。这样就相当于随机舍弃了一些点可能会导致丢失信息。

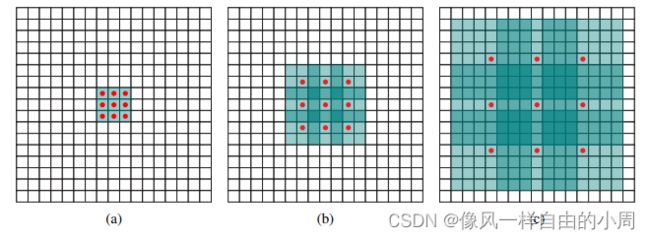
继续盗图如何理解扩张卷积(dilated convolution)

好了，那Pytroch咋实现呢，有一个参数dilation就是用来干这个事的。

这里面的link链接这里提供一下：Convolution arithmetic

如果dilation取1就是普通的2D卷积

m = nn.Conv2d(inplane, 33, 3, dilation=2)

8.反卷积

在深度学习中，如果使用卷积得到的特征尺寸是小于等于原尺寸的，且很多时候，我们使用卷积得到的特征尺寸是远小于输入图像尺寸的，但是对于某些特定的任务需要我们最终得到的特征尺寸和输入图像尺寸大小一样咋办（比如语义分割、变化检测）？还能咋办，提高特征图大小呗。常见的方法有上采样、反卷积、反池化等。

下面简单介绍一下反卷积。反卷积又被称为转置卷积，为啥叫转置，不是求逆涉及到具体的数学计算，这里简单说一下，卷积计算可以看为$CA=B$这种卷积计算，从A变成了B，现在想要从B变成A咋办呢，C^-1B=A 通过这一个可逆运算就行了吧，但是这个求逆是不是太复杂了，能否求出来还是一个问题，于是用C^TB=A来进行代替（纯属个人瞎bb，网上没有这种说法，个人猜的）这就是为啥叫转置卷积。这个C张啥样不用太纠结，反正接下来就会介绍反卷积计算过程，不过从这个公式就可以看出来，反卷积的目的是为了获得A的尺寸不是去为了还原A的具体数值。

反卷积通俗详细解析与nn.ConvTranspose2d重要参数解释 这篇文章对于Pytroch中的参数解释实在是写的太好了，推荐读一下，我下面总结一下。

反卷积要干的事主要有两件：

• 对输入根据Padding和stride进行填充扩大输入图像/特征的大小使得进行正常卷积后得到的特征大小为预想的正常大小，这里的padding和正常的2D卷积一样操作只不过数值上有些差别，stride和正常的2D卷积中的dilation类似，参考空洞卷积部分。
• 选择一个新的卷积核进行正常的2D卷积操作。这里的正常的卷积步长固定为1（我在网上找了半天卷积核反卷积详细说明终于找到了有说明咋进行正常卷积的了）

下面简单看一下Pytroch中的反卷积实现函数nn.ConvTranspose2d。

反卷积参数动态演示受不了啦，pytroch官方文档就提供了参数的动态演示，还等啥呢。

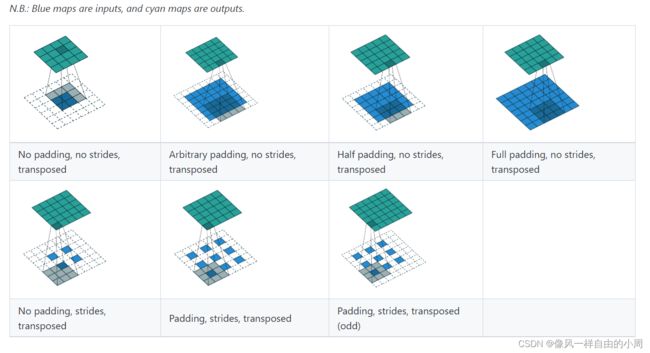
这里的padding参数就是在外围填充，但是填充量为 dilation * (kernel_size - 1) - padding，stride参数类似于dilation只不过这里的stride是在Input上进行填充。output_padding是在右和下侧各填充一行，添加这个参数是因为在扩大图像过程中有些大小无法获得故添加该参数。


好啦，Pytroch实现就不多说啥了，函数还有参数含义都告诉你了，相信你自己可以实现。

9.Involution

没咋见过，后续了解了再写。

参考文献

1.带你认识9种常用卷积神经网络
2.CNN入门讲解：什么是卷积（Convolution）
3.【DL笔记6】从此明白了卷积神经网络（CNN）
4.3D卷积（3D Convolution）
5.1*1卷积层
6.为什么用1*1卷积层代替全连接层？
7.CNN 入门讲解：什么是全连接层（Fully Connected Layer）?
8.Separable Convolution简介
9.深度可分离卷积
10.卷积网络参数量和计算（FLOPs）的计算公式及代码
11.分组卷积（Group Convolution）
12.如何理解扩张卷积(dilated convolution)
13.转置卷积定义
14.ConvTranspose2d原理，深度网络如何进行上采样？