线性代数-向量空间
线性代数-向量空间
-
- 向量空间
-
- 向量空间
- 张成空间
-
- 等价向量组
- 最大无关组
- 向量组的秩
- 向量空间的基
-
- 基与坐标
- 向量空间的维度
- 点积(数量积)
-
- 欧几里得空间
- 长度
- 角度
- 新的运算
- 点积的定义
- 长度/角度与自然基
- 点积的性质
- 欧氏距离和余弦距离
- 小结
向量空间
向量空间
向量空间的严格定义:
设 V V V 为一向量组,如果 V V V 非空,且 V V V 对于向量的加法以及数乘两种运算封闭,那么就称 V V V 为
向量空间。
所谓封闭,是指在 V V V 中向量进行数乘和加减,其结果依然在 V V V 中。具体的说,就是:
- 若 a ⃗ ∈ V , b ⃗ ∈ V , \vec{a} \in V, \vec{b} \in V, a∈V,b∈V, 则 a ⃗ + b ⃗ ∈ V \vec{a} + \vec{b} \in V a+b∈V
- 若 a ⃗ ∈ V , k ∈ R , \vec{a} \in V, k \in \mathbb{R}, a∈V,k∈R, 则 k a ⃗ ∈ V k\vec{a} \in V ka∈V
所有 n n n 维向量构成的集合是一个
向量空间R n \mathbb{R}^n Rn:
R n = { ( x 1 , x 2 , . . . , x n ) ∣ n ∈ N , x n ∈ R } \mathbb{R}^n = \{(x_1,x_2,...,x_n) | n \in \mathbb{N}, x_n \in \mathbb{R}\} Rn={(x1,x2,...,xn)∣n∈N,xn∈R}
张成空间
某 向量组 A = { v 1 ⃗ , v 2 ⃗ , . . . , v p ⃗ } A = \{\vec{v_1}, \vec{v_2}, ..., \vec{v_p}\} A={v1,v2,...,vp}, 其所有 线性组合 构成的集合为 向量空间, 也称为向量组 A A A 的
张成空间, 记为 s p a n ( v 1 ⃗ , v 2 ⃗ , . . . , v p ⃗ ) span(\vec{v_1}, \vec{v_2}, ..., \vec{v_p}) span(v1,v2,...,vp), 即:
V = s p a n ( v 1 ⃗ , v 2 ⃗ , . . . , v p ⃗ ) = { k 1 v 1 ⃗ + k 2 v 2 ⃗ + . . . + k p v p ⃗ , k 1 , 2 , . . . , p ∈ R } V = span(\vec{v_1}, \vec{v_2}, ..., \vec{v_p}) = \{k_1\vec{v_1} + k_2\vec{v_2} + ... + k_p\vec{v_p}, k_{1,2,...,p} \in \mathbb{R}\} V=span(v1,v2,...,vp)={k1v1+k2v2+...+kpvp,k1,2,...,p∈R}
也称 s p a n ( v 1 ⃗ , v 2 ⃗ , . . . , v p ⃗ ) span(\vec{v_1}, \vec{v_2}, ..., \vec{v_p}) span(v1,v2,...,vp) 为向量组 A A A 所张成
等价向量组
设有两个 向量组 A = { a 1 ⃗ , a 2 ⃗ , . . . , a m ⃗ } A = \{\vec{a_1},\vec{a_2},...,\vec{a_m}\} A={a1,a2,...,am} 及 B = { b 1 ⃗ , b 2 ⃗ , . . . , b n ⃗ } B = \{\vec{b_1},\vec{b_2},...,\vec{b_n}\} B={b1,b2,...,bn}, 若 B B B 组中的每个向量都能由向量组 A A A
线性表示, 则称向量组 B B B 能由向量组 A A A 线性表示.
若向量组 A A A 与向量组 B B B 能互相线性表示, 则称这两个向量组等价, 也可以说 A A A 和 B B B 是等价向量组
等价向量组 的 张成空间 是相等的
假设有两个向量组
A = { a 1 ⃗ , a 2 ⃗ , . . . , a m ⃗ } , B = { b 1 ⃗ , b 2 ⃗ , . . . , b n ⃗ } A = \{\vec{a_1},\vec{a_2},...,\vec{a_m}\}, B = \{\vec{b_1},\vec{b_2},...,\vec{b_n}\} A={a1,a2,...,am},B={b1,b2,...,bn}
则
A 和 B 等 价 ⟺ s p a n ( A ) = s p a n ( B ) A 和 B 等价 \iff span(A) = span(B) A和B等价⟺span(A)=span(B)
最大无关组
设有 向量组 A A A, 如果在 A A A 中能选出 r r r 个向量 a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ \vec{a_1},\vec{a_2},...,\vec{a_r} a1,a2,...,ar 满足:
- 向量组 A 0 = { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } A_0 = \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} A0={a1,a2,...,ar} 线性无关
- 向量组 A A A 中任意 r + 1 r + 1 r+1 个向量 (如果 A A A 中有 r + 1 r + 1 r+1 个向量的话) 都 线性相关, 那么成向量组 A 0 A_0 A0 是向量组 A A A 的一个
最大线性无关组, 简称最大无关组
- 包含零向量的向量组一定不是
最大无关组
向量组的秩
假设 向量组 A A A 的 最大无关组 为:
A 0 = { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } A_0 = \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} A0={a1,a2,...,ar}
A 0 A_0 A0 的向量个数 r r r 称为向量组 A A A 的秩, 记做 r a n k ( A ) rank(A) rank(A), 有时也记做 r ( A ) r(A) r(A)
- 不变的
秩反应了向量组的 复杂程度. - 只包含零向量的向量组的
秩为 0
向量空间的基
V V V 为 向量空间, 如果其中的某向量组:
A = { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } A = \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} A={a1,a2,...,ar}
是 V V V 的 最大无关组, 那么向量组 A A A 被称为向量空间 V V V 的一个基
- 只包含零向量的向量空间 { ( 0 0 ) } \left \{\begin{pmatrix} 0 \\ 0 \end{pmatrix}\right\} {(00)} 该向量空间没有
基
自然基, 指由某一维为 1 其余维都是 0 的向量组成的一组基, 且该向量组是线性无关的.
所有的 R n \mathbb{R^n} Rn 都有自然基:
e 1 ⃗ = ( 1 0 ⋮ 0 ) , e 2 ⃗ = ( 0 1 ⋮ 0 ) , ⋯ , e n ⃗ = ( 0 0 ⋮ 1 ) \vec{e_1} = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}, \vec{e_2} = \begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{pmatrix}, \cdots, \vec{e_n} = \begin{pmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{pmatrix} e1=⎝⎜⎜⎜⎛10⋮0⎠⎟⎟⎟⎞,e2=⎝⎜⎜⎜⎛01⋮0⎠⎟⎟⎟⎞,⋯,en=⎝⎜⎜⎜⎛00⋮1⎠⎟⎟⎟⎞
基与坐标
在 向量空间 V V V 中取一个 基 { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} {a1,a2,...,ar}, 那么 V V V 中的某个向量 x ⃗ \vec{x} x 可唯一地表示为:
x ⃗ = k 1 a 1 ⃗ + k 2 a 2 ⃗ + ⋯ + k r a r ⃗ \vec{x} = k_1\vec{a_1} + k_2\vec{a_2} + \cdots + k_r\vec{a_r} x=k1a1+k2a2+⋯+krar
其中, ( k 1 , k 2 , . . . , k r ) (k_1,k_2,...,k_r) (k1,k2,...,kr) 称为向量 x ⃗ \vec{x} x 在基 { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} {a1,a2,...,ar} 中的坐标. 如果将基 { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} {a1,a2,...,ar} 简称为基 a a a 的话, 那么 x ⃗ \vec{x} x 还可以写作:
x ⃗ = ( k 1 k 2 ⋮ k r ) a \vec{x} = \begin{pmatrix} k_1 \\ k_2 \\ \vdots \\ k_r \end{pmatrix}_a x=⎝⎜⎜⎜⎛k1k2⋮kr⎠⎟⎟⎟⎞a
其中, 下标 a a a 指明该坐标系的基
向量空间的维度
假设向量空间 V V V 的 基:
A = { a 1 ⃗ , a 2 ⃗ , . . . , a r ⃗ } A = \{\vec{a_1},\vec{a_2},...,\vec{a_r}\} A={a1,a2,...,ar}
则 A A A 的 秩 r r r 称为该向量空间的维度, 或者称 V V V 为 r r r 维向量空间
- n n n 维向量可以张成 0 n 0~n 0 n 维的向量空间
点积(数量积)
欧几里得空间
欧 几 里 得 空 间 = 向 量 空 间 + 长 度 + 角 度 欧几里得空间 = 向量空间 + 长度 + 角度 欧几里得空间=向量空间+长度+角度
长度
根据勾股定理可得
∣ ∣ a ⃗ ∣ ∣ = a 1 2 + a 2 2 ||\vec{a}|| = \sqrt{a_1^2 + a_2^2} ∣∣a∣∣=a12+a22
角度
定义: 在 R 2 \mathbb{R^2} R2 中, 两个向量间的夹角 θ \theta θ, 该夹角的取值范围在 0 ≤ θ ≤ π 0 \leq \theta \leq \pi 0≤θ≤π
注意到 cos x \cos{x} cosx 函数在 0 ≤ θ ≤ π 0 \leq \theta \leq \pi 0≤θ≤π 这个范围是单调的.
根据欧氏集合中的余弦定理可以得到如下 结论
cos θ = a 1 b 1 + a 2 b 2 ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ \cos{\theta} = \frac{a_1b_1 + a_2b_2}{||\vec{a}|| ||\vec{b}||} cosθ=∣∣a∣∣∣∣b∣∣a1b1+a2b2
证明:
根据欧氏几何中余弦定理, 我们可以得到:
A B → 2 = O A → 2 + O B → 2 − 2 O A → ⋅ O B → cos θ \overrightarrow{AB}^2 = \overrightarrow{OA}^2 + \overrightarrow{OB}^2 - 2\overrightarrow{OA} \cdot \overrightarrow{OB} \cos{\theta} AB2=OA2+OB2−2OA⋅OBcosθ
上式可以通过向量来计算:
∣ ∣ a ⃗ − b ⃗ ∣ ∣ 2 = ∣ ∣ a ⃗ ∣ ∣ 2 + ∣ ∣ b ⃗ ∣ ∣ 2 − 2 ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ cos θ ||\vec{a} - \vec{b}||^2 = ||\vec{a}||^2 + ||\vec{b}||^2 - 2||\vec{a}|| ||\vec{b}|| \cos{\theta} ∣∣a−b∣∣2=∣∣a∣∣2+∣∣b∣∣2−2∣∣a∣∣∣∣b∣∣cosθ
新的运算
假设定义一个新的运算方式, 将之称为向量的 点积
a ⃗ ⋅ b ⃗ = ( a 1 , a 2 ) ⋅ ( b 1 , b 2 ) = a 1 b 1 + a 2 b 2 \vec{a} \cdot \vec{b} = (a_1, a_2) \cdot (b_1, b_2) = a_1b_1 + a_2b_2 a⋅b=(a1,a2)⋅(b1,b2)=a1b1+a2b2
那么向量空间 R 2 \mathbb{R^2} R2 中的长度和角度的计算就可以通过 点积 来完成:
- 长度
∣ ∣ a ⃗ ∣ ∣ = a 1 2 + a 2 2 = a 1 a 1 + a 2 a 2 = a ⃗ ⋅ a ⃗ ||\vec{a}|| = \sqrt{a_1^2 + a_2^2} = \sqrt{a_1a_1 + a_2a_2} = \sqrt{\vec{a} \cdot \vec{a}} ∣∣a∣∣=a12+a22=a1a1+a2a2=a⋅a
- 角度
cos θ = a 1 b 1 + a 2 b 2 ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ \cos{\theta} = \frac{a_1b_1 + a_2b_2}{||\vec{a}|| ||\vec{b}||} = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| ||\vec{b}||} cosθ=∣∣a∣∣∣∣b∣∣a1b1+a2b2=∣∣a∣∣∣∣b∣∣a⋅b
点积的定义
向量 x ⃗ = ( x 1 x 2 ⋮ x n ) \vec{x} = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} x=⎝⎜⎜⎜⎛x1x2⋮xn⎠⎟⎟⎟⎞ 和 y ⃗ = ( y 1 y 2 ⋮ y n ) \vec{y} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{pmatrix} y=⎝⎜⎜⎜⎛y1y2⋮yn⎠⎟⎟⎟⎞ 的
点积(dot product), 定义为:
x ⃗ ⋅ y ⃗ = x 1 y 1 + ⋯ + x n y n = ∑ i = 1 n x i y i \vec{x} \cdot \vec{y} = x_1y_1 + \cdots + x_ny_n = \sum_{i=1}^{n}x_iy_i x⋅y=x1y1+⋯+xnyn=i=1∑nxiyi
点积还可以称为数量积或者标量积, 这是因为两个向量通过点积运算之后的结果是数量(标量).
长度/角度与自然基
通过点积计算长度/角度时, 向量的坐标必须在 自然基 下.
点积的性质
点积具有以下运算性质:
- 交换律: a ⃗ ⋅ b ⃗ = b ⃗ ⋅ a ⃗ \vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} a⋅b=b⋅a
- 数乘结合律: ( k a ⃗ ) ⋅ b ⃗ = k ( b ⃗ ⋅ a ⃗ ) (k\vec{a}) \cdot \vec{b} = k(\vec{b} \cdot \vec{a}) (ka)⋅b=k(b⋅a)
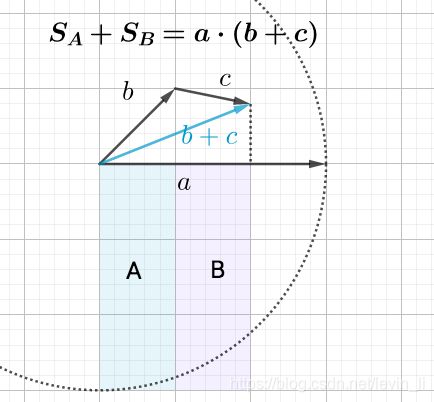
- 分配律: ( a ⃗ + b ⃗ ) ⋅ c ⃗ = a ⃗ ⋅ c ⃗ + b ⃗ ⋅ c ⃗ (\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} (a+b)⋅c=a⋅c+b⋅c
以下对 数乘结合律 和 分配律 的证明太惊艳了, 必须记录下来
- 数乘结合律
根据 点积 可推出
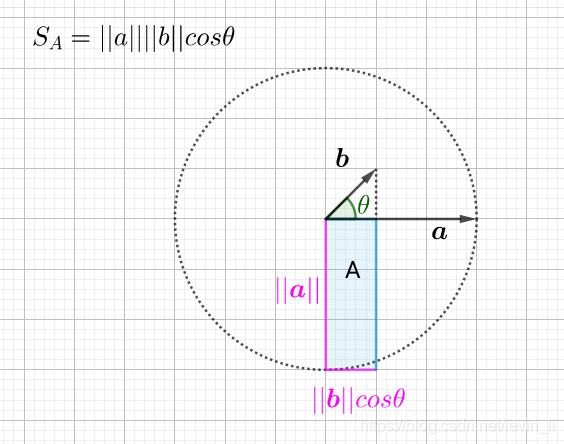
cos θ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ ⟹ a ⃗ ⋅ b ⃗ = ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ cos θ \cos{\theta} = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| ||\vec{b}||} \implies \vec{a} \cdot \vec{b} = ||\vec{a}|| ||\vec{b}|| \cos{\theta} cosθ=∣∣a∣∣∣∣b∣∣a⋅b⟹a⋅b=∣∣a∣∣∣∣b∣∣cosθ
其中 ∣ ∣ b ⃗ ∣ ∣ cos θ {\color{Red}||\vec{b}|| \cos{\theta}} ∣∣b∣∣cosθ 可以看做 b ⃗ \vec{b} b 在 \vec{a} 上的投影

所以, 可以把 a ⃗ ⋅ b ⃗ \vec{a} \cdot \vec{b} a⋅b 看做矩形 A A A 的面积:
自然, 其中一条边放大 k k k 倍, 则面积增大 k k k 倍
( k a ⃗ ) ⋅ b ⃗ = k ( b ⃗ ⋅ a ⃗ ) (k\vec{a}) \cdot \vec{b} = k(\vec{b} \cdot \vec{a}) (ka)⋅b=k(b⋅a)
- 分配律
欧氏距离和余弦距离
- 欧氏距离 表示两个向量间的距离远近;
- 余弦距离 表示两个向量间的关系远近;
正交是线性代数的概念, 是垂直这一直观概念的推广, 若两向量的内积为 0, 则称他们是正价的.
小结
在该章中有很多概念很容易混淆, 他们是:
- 向量空间: 非空, 由若干向量组成(向量组), 这些向量满足加法/数乘封闭
- 张成空间: 由 向量组 进行所有 线性组合 后得到的 向量空间
- 最大无关组: 从 向量组 中选取满足 线性无关 的向量, 且这些向量可以 线性表示 向量组中其他的任意向量
- 秩: 最大无关组的个数
- 基: 就是最大无关组. 引入次概念主要是为了后面的坐标概念