神经网络与深度学习系列 -反向传播算法
矩阵的在神经网络中的应用
本系列的上一节介绍了梯度下降算法,本节将介绍反向传播算法。利用矩阵在神经网络中,可以大大简化公式的复杂性,同时矩阵运算在反向传播中使用起来极为方便。
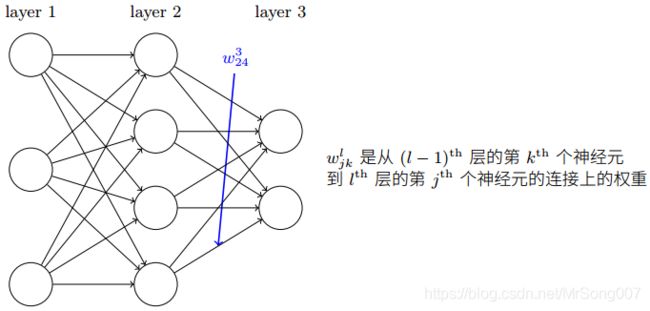
上图给出了神经网络中对权重的标注方式, w j k l w_{jk}^l wjkl表示从 ( l − i ) t h {(l-i)}^{th} (l−i)th 层的第 k t h k^{th} kth 个神经元到 l t h {l}^{th} lth 层的第 j t h j^{th} jth 个神经元的连接上的权重。
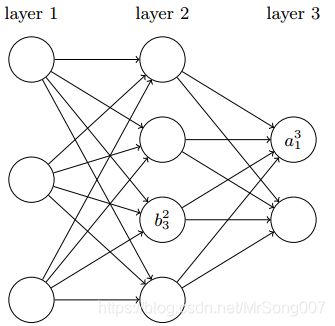
上图给出了神经网络中对偏置和激活值的标注方式, b j l b_j^l bjl 表示在 l t h l^{th} lth层第 j t h j^{th} jth个神经元的偏置; a j l a_j^l ajl 表示在 l t h l^{th} lth层第 j t h j^{th} jth个神经元的激活。
那么, l t h l^{th} lth层的第 j t h j^{th} jth个神经元的激活值 a j l a_j^l ajl 可以和 ( l − 1 ) t h (l-1)^{th} (l−1)th层的激活值通过S型函数联系起来:
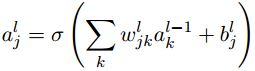
其中求和是在 ( l − 1 ) t h (l-1)^{th} (l−1)th层的所有k个神经元上进行。
定义权重矩阵 w l w^l wl, w l w^l wl的元素为连接到 l t h l^{th} lth层神经元的所有权重;
定义偏置向量 b l b^l bl, b l b^l bl的元素为 l t h l^{th} lth层神经元的所有偏置;
以上方程就可以写成矩阵的形式:
![]()
上式括号中的 w l a l − 1 + b l = z l w^la^{l-1}+b^l=z^l wlal−1+bl=zl称为带权输入。第 l l l层的第 j j j个神经元的激活函数的带权输入为, z j l = ∑ k w j k l a k l − 1 + b j l z_j^{l}=\sum_{k}w_{jk}^{l}a_k^{l-1}+b_j^{l} zjl=∑kwjklakl−1+bjl
反向传播的四个基本方程
误差
反向传播的目的就是计算梯度下降中的偏导数 ∂ C / ∂ w j k l \partial C/\partial w_{jk}^l ∂C/∂wjkl和 ∂ C / ∂ b j l \partial C/\partial b_{j}^l ∂C/∂bjl,其中需要用到一个中间量 δ j l \delta_j^l δjl,
定义 δ j l \delta_j^l δjl为在 l t h l^{th} lth层第 j t h j^{th} jth个神经元上的误差。
误差的概念该如何理解? 首先明确: w j k l w_{jk}^l wjkl 和 b j l b_j^l bjl的微小变化会引起带权输入 z j l z_j^l zjl 的变化,当带权输入 z j l z_j^l zjl发生一个微小变化 Δ z j l \Delta z_j^l Δzjl, 在整个代价函数 C C C上引起的变化为 ∂ C ∂ z j l Δ z j l \frac{\partial C}{\partial z_{j}^l}\Delta z_j^l ∂zjl∂CΔzjl。
假设我们尝试优化代价函数,试着找到一个让代价函数 C C C更小的微小变化 Δ z j l \Delta z_j^l Δzjl(该变化当然也是由 w j k l w_{jk}^l wjkl 和 b j l b_j^l bjl引起的),如果 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^l} ∂zjl∂C有一个很大的值(或正或负),我们可以通过选择与 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^l} ∂zjl∂C符号相反的 Δ z j l \Delta z_j^l Δzjl来使代价函数减小;如果 ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^l} ∂zjl∂C接近0, ∂ C ∂ z j l Δ z j l \frac{\partial C}{\partial z_{j}^l}\Delta z_j^l ∂zjl∂CΔzjl也接近0,则 Δ z j l \Delta z_j^l Δzjl就没有必要变化,即使变化在代价函数上引起的影响也微乎其微。
所以说, ∂ C ∂ z j l \frac{\partial C}{\partial z_{j}^l} ∂zjl∂C会影响到 Δ z j l \Delta z_j^l Δzjl(即 w j k l w_{jk}^l wjkl 和 b j l b_j^l bjl)的变化, 所以有一种启发式的认识: δ j l = ∂ C ∂ z j l = ∂ C ∂ a j l σ ′ ( z j l ) \delta_{j}^l=\frac{\partial C}{\partial z_{j}^l}=\frac{\partial C}{\partial a_{j}^l}\sigma'(z_{j}^l) δjl=∂zjl∂C=∂ajl∂Cσ′(zjl)是神经元上微小变化的度量,称为是神经元上误差的度量。
四个方程
- 输出层误差方程:
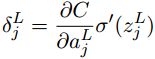
- 用下一层的误差 δ l + 1 \delta^{l+1} δl+1来计算当前层的误差 δ l \delta^{l} δl:
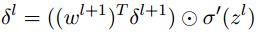
- 代价函数关于网络中任意偏置的改变率:

- 代价函数关于任何一个权重的改变率:
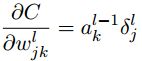
根据方程1,当 σ ( z j L ) \sigma(z_j^L) σ(zjL)近似为0或者1的时候, σ ′ ( z j L ) \sigma^{\prime}(z_j^L) σ′(zjL) ≈ \approx ≈ 0,那么最终层的权重学习缓慢,这种情况称为神经元饱和。
四个方程的推导
方程1推导:
首先根据误差的定义有:
δ j L = ∂ C ∂ z j L \delta_j^L=\frac{\partial C}{\partial z_{j}^L} δjL=∂zjL∂C,
应用链式法则:
δ j L = ∂ C ∂ a j L ∂ a j L ∂ z j L \delta_j^L=\frac{\partial C}{\partial a_{j}^L}\frac{\partial a_{j}^L}{\partial z_{j}^L} δjL=∂ajL∂C∂zjL∂ajL
因为 a j L = σ ( z j L ) a_j^L=\sigma(z_j^L) ajL=σ(zjL),所以上述方程变成:
δ j L = ∂ C ∂ a j L σ ′ ( z j L ) \delta_j^L=\frac{\partial C}{\partial a_{j}^L}\sigma^{\prime}(z_j^L) δjL=∂ajL∂Cσ′(zjL) ,方程1得证。
方程2推导:
根据误差的定义有:
δ j l = ∂ C ∂ z j l \delta_j^l=\frac{\partial C}{\partial z_{j}^l} δjl=∂zjl∂C
引用链式法则:
δ j l = ∂ C ∂ z j l = ∑ k ∂ C ∂ z k l + 1 ∂ z k l + 1 ∂ z j l = ∑ k ∂ z k l + 1 ∂ z j l δ k l + 1 \delta_j^l=\frac{\partial C}{\partial z_{j}^l}=\sum_{k}\frac{\partial C}{\partial z_{k}^{l+1}}\frac{\partial z_{k}^{l+1}}{\partial z_{j}^l}=\sum_{k}\frac{\partial z_{k}^{l+1}}{\partial z_{j}^l}\delta_k^{l+1} δjl=∂zjl∂C=∑k∂zkl+1∂C∂zjl∂zkl+1=∑k∂zjl∂zkl+1δkl+1
已知: z j l + 1 = ∑ k w j k l + 1 a k l + b j l + 1 = ∑ k w j k l + 1 σ ( z k l ) + b j l + 1 z_j^{l+1}=\sum_{k}w_{jk}^{l+1}a_k^l+b_j^{l+1}=\sum_{k}w_{jk}^{l+1}\sigma(z_k^l)+b_j^{l+1} zjl+1=∑kwjkl+1akl+bjl+1=∑kwjkl+1σ(zkl)+bjl+1。作微分,得到:
∂ z k l + 1 ∂ z j l = w k j l + 1 σ ′ ( z j l ) \frac{\partial z_{k}^{l+1}}{\partial z_{j}^l}=w_{kj}^{l+1}\sigma^{\prime}(z_j^l) ∂zjl∂zkl+1=wkjl+1σ′(zjl)
带入得到:
δ j l = ∑ k w k j l + 1 δ k l + 1 σ ′ ( z j l ) \delta_j^l=\sum_{k}w_{kj}^{l+1}\delta_k^{l+1}\sigma^{\prime}(z_j^l) δjl=∑kwkjl+1δkl+1σ′(zjl) ,方程2得证。
方程3推导:
引用链式法则:
∂ C ∂ b j l = ∂ C ∂ a j l ∂ a j l ∂ b j l \frac{\partial C}{\partial b_{j}^l}=\frac{\partial C}{\partial a_{j}^l}\frac{\partial a_{j}^l}{\partial b_{j}^l} ∂bjl∂C=∂ajl∂C∂bjl∂ajl
根据方程1已知: δ j l = ∂ C ∂ a j l σ ′ ( z j l ) \delta_j^l=\frac{\partial C}{\partial a_{j}^l}\sigma^{\prime}(z_j^l) δjl=∂ajl∂Cσ′(zjl)
若能证明: σ ′ ( z j l ) = ∂ a j l ∂ b j l \sigma^{\prime}(z_j^l)=\frac{\partial a_{j}^l}{\partial b_{j}^l} σ′(zjl)=∂bjl∂ajl,则方程3得证;
已知 a j l = σ ( z j l ) a_j^l=\sigma(z_j^l) ajl=σ(zjl) 和 z j l = ∑ k w j k l a k l + b j l z_j^{l}=\sum_{k}w_{jk}^{l}a_k^l+b_j^{l} zjl=∑kwjklakl+bjl
则有 ∂ a j l ∂ b j l = ∂ σ ( z j l ) ∂ b j l = σ ′ ( z j l ) \frac{\partial a_{j}^l}{\partial b_{j}^l}=\frac{\partial \sigma(z_j^l)}{\partial b_{j}^l}=\sigma^{\prime}(z_j^l) ∂bjl∂ajl=∂bjl∂σ(zjl)=σ′(zjl) ,方程3得证;
方程4推导:
引用链式法则:
∂ C ∂ w j k l = ∂ C ∂ z j l ∂ z j l ∂ w j k l = δ j l ∂ z j l ∂ w j k l \frac{\partial C}{\partial w_{jk}^l}=\frac{\partial C}{\partial z_{j}^l}\frac{\partial z_{j}^l}{\partial w_{jk}^l}=\delta_j^l\frac{\partial z_{j}^l}{\partial w_{jk}^l} ∂wjkl∂C=∂zjl∂C∂wjkl∂zjl=δjl∂wjkl∂zjl
若能求得: ∂ z j l ∂ w j k l = a k l − 1 \frac{\partial z_{j}^l}{\partial w_{jk}^l}=a_k^{l-1} ∂wjkl∂zjl=akl−1,即得证;
其中 z j l = ∑ k w j k l a k l − 1 + b j l z_j^{l}=\sum_{k}w_{jk}^{l}a_k^{l-1}+b_j^{l} zjl=∑kwjklakl−1+bjl,代入上式左侧得到: ∂ z j l ∂ w j k l = a k l − 1 \frac{\partial z_j^l}{\partial w_{jk}^l}=a_k^{l-1} ∂wjkl∂zjl=akl−1,方程4得证;
反向传播算法
前边说过,反向传播的目的就是计算梯度下降算法中的偏导数 ∂ C / ∂ w j k l \partial C/\partial w_{jk}^l ∂C/∂wjkl和 ∂ C / ∂ b j l \partial C/\partial b_{j}^l ∂C/∂bjl,那么显式的用算法步骤描述出来如下:
- 输入 x x x:为输入层设置对应的激活值 a 1 a^1 a1;
- 前向传播:对每个 l = 2 , 3 , . . . L l=2,3,...L l=2,3,...L 计算相应的 z l = w l a l − 1 + b l z^l=w^la^{l-1}+b^l zl=wlal−1+bl和 a l = σ ( z l ) a^l=\sigma(z^l) al=σ(zl);
- 输出层误差: δ L \delta^L δL: 计算向量 δ L = ∇ a C ⨀ σ ′ ( z L ) \delta^L=\nabla_aC\bigodot\sigma^{\prime}(z^L) δL=∇aC⨀σ′(zL);
- 反向传播误差:对每个 l = L − 1 , L − 2 , . . . , 2 l=L-1,L-2,...,2 l=L−1,L−2,...,2,计算 δ l = ( ( w l + 1 ) T δ l + 1 ) ⨀ σ ′ ( z l ) \delta^l=((w^{l+1})^T\delta^{l+1})\bigodot\sigma^{\prime}(z^l) δl=((wl+1)Tδl+1)⨀σ′(zl);
- 输出:代价函数的梯度由 ∂ C ∂ w j k l = a k l − 1 δ j l \frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}\delta_j^l ∂wjkl∂C=akl−1δjl和 ∂ C ∂ b j l = δ j l \frac{\partial C}{\partial b_{j}^l}=\delta_j^l ∂bjl∂C=δjl得出。
检视这个算法流程,我们可以看出它为何被称为反向传播算法,误差向量 δ l \delta^l δl的计算是从最后一层开始,逐步向前传递。
反向传播算法在随机梯度下降算法的应用:
在实践中,通常将反向传播算法和随机梯度下降算法进行结合使用,对于一个给定的大小为 m m m的小批量数据,反向传播算法在随机梯度下降算法的应用步骤为:
- 输入训练样样本的集合;
- 对每个训练样本 x x x: 设置对应的输入激活 a x , 1 a^{x,1} ax,1,并执行下面的步骤:
a. 前向传播:对每个 l = 2 , 3 , . . . L l=2,3,...L l=2,3,...L,计算相应的 z x , l = w l a x , l − 1 + b l z^{x,l}=w^la^{x,l-1}+b^l zx,l=wlax,l−1+bl和 a x , l = σ ( z x , l ) a^{x,l}=\sigma(z^{x,l}) ax,l=σ(zx,l);
b. 输出误差: δ x , L \delta^{x,L} δx,L: 计算向量 δ x , L = ∇ a C x ⨀ σ ′ ( z x , L ) \delta^{x,L}=\nabla_aC_x\bigodot\sigma^{\prime}(z^{x,L}) δx,L=∇aCx⨀σ′(zx,L);
c. 反向传播误差:对每个 l = L − 1 , L − 2 , . . . , 2 l=L-1,L-2,...,2 l=L−1,L−2,...,2,计算 δ x , l = ( ( w l + 1 ) T δ x , l + 1 ) ⨀ σ ′ ( z x , l ) \delta^{x,l}=((w^{l+1})^T\delta^{x,l+1})\bigodot\sigma^{\prime}(z^{x,l}) δx,l=((wl+1)Tδx,l+1)⨀σ′(zx,l); - 梯度下降:对每个 l = L − 1 , L − 2 , . . . , 2 l=L-1,L-2,...,2 l=L−1,L−2,...,2,根据 w l = w l − η m ∑ x δ x , l ( a x , l − 1 ) T w^l=w^l-\frac{\eta}{m}\sum_x\delta^{x,l}(a^{x,l-1})^T wl=wl−mη∑xδx,l(ax,l−1)T和 b l = b l − η m ∑ x δ x , l b^l=b^l-\frac{\eta}{m}\sum_x\delta^{x,l} bl=bl−mη∑xδx,l
本系列的下一节将通过代码的实现来理解上述算法的实际应用过程;