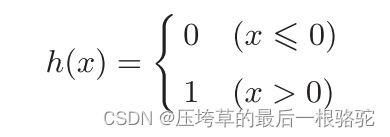深度学习——神经网络

2 神经网络

2-1 复习感知机的结构

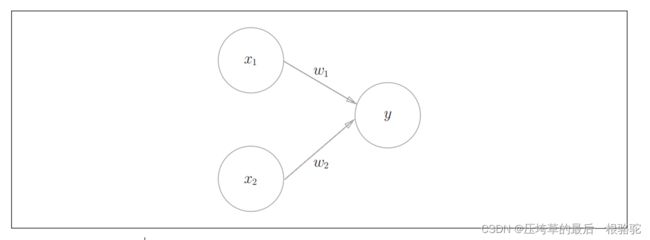
感知机接收x1和x2两个输入信号，输出y。如果用数学式来表示图3-2中的感知机。
（一式）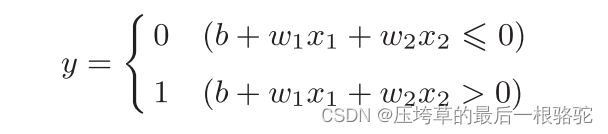
b是被称为偏置的参数，用于控制神经元被激活的容易程度。w1，w2表示各个信号的权重参数。此外添加了权重为b的输入信号1，
如果这个总和超过0，则输出1，否则输出0。
我们用一个函数来表示这种分情况的动作（超过0则输出1，否则输出0）。
引入新函数h(x)：
h（x）： y = h(b + w1x1 + w2x2) （二式）

（三式）
（二式）与（三式）起到了与（一式）相同的作用。

2-2 激活函数

定义：刚才登场的h（x）函数会将输入信号的总和转换为输出信号，这种函数
一般称为激活函数（activation function）。
————————————————————
将上述的（二式）改写成（四式与五式）：
a = b + w1x1 + w2x2 （四式）
y = h(a) （五式）
首先，（四式）计算加权输入信号和偏置的总和，记为a。然后，（五式）用h(x)函数将a转换为输出y。
————————————————————
（明确显示出激活函数的计算过程）

激活函数是连接感知机和神经网络的桥梁。
“朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数A 的模型。“多层感知机”是指神经网络，即使用 sigmoid函数（后述）等平滑的激活函数的多层网络。
（式三）表示的激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为“阶跃函数”感知机中使用了阶跃函数作为激活函数。也就是说，在激活函数的众多候选函数中，感知机使用了阶跃函数。
如果将激活函数从阶跃函数换成其他函数，就可以表示一个神经网络了。

sigmoid 函数

神经网络中经常使用的一个激活函数就是（六式）sigmoid函数

神经网络中用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。感知机和神经网络的主要区别就在于这个激活函数。
——————————————————————————————————
对于阶跃函数：当输入超过0时，输出1，否则输出0.

使用numpy 数组作为参数实现阶跃函数：

>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0
>>> y
array([False, True, True], dtype=bool)

由于得到数组y是一个bool类型的，我们希望得到阶跃函数是输出1或者0，因此需要把数组y的元素转换为int型，使用函数astype（）

>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])

——————————————————————————————————

阶跃函数的图像：

import numpy as np
import matplotlib.pylab as plt
def step_function(x):
 return np.array(x > 0, dtype=‘i4’)
x = np.arange(-4.0, 4.0, 0.2)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.2, 1.2) # 指定y轴的范围
plt.show()

(下图为阶跃函数的图形）
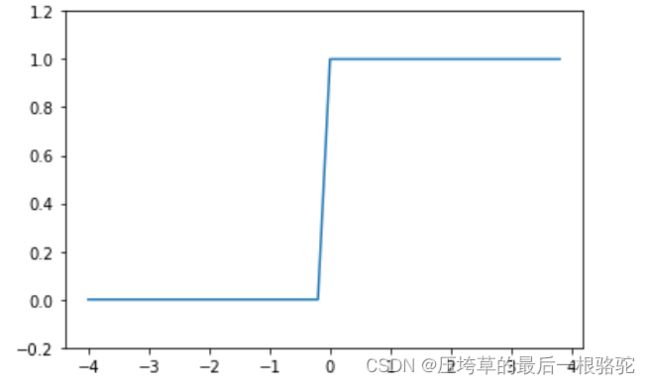阶跃函数以0为界，输出从0切换为1（或者从1切换为0）。它的值呈阶梯式变化，所以称为阶跃函数。

sigmoid函数的实现

def sigmoid(x):
    return 1/(1+np.exp(-x))
x=np.arange(-4.0,4.0,0.2)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1,1.2)
plt.show()

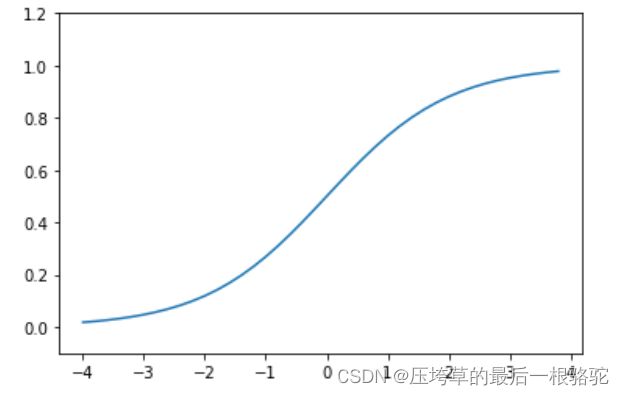
sigmoid函数图像：

“光滑”的曲线

对比sigmoid函数与阶跃函数：

①感知机中神经元之间流动的是0或1的二元信号，而神经网络中流动的是连续的实数值信号。
②阶跃函数只在传输（0/1）两个动作，sigmoid函数可以调整。
③两个函数的输出信号的值都在0和1之间。

什么是非线性的函数

阶跃函数和sigmoid函数都是非线性的，何为线性函数：当输出值是输入值的常数倍的时候，列入f（x）=C*x（C为常数），神将网络的激活函数必须使用非线性函数，不然神经网络的层数就没有意义。
举例为什么没有意义：
使用线性函数时没有隐藏层的神经网络。如F（X）=Cx作为激活函数时，y（x）=F（F（F（x）））的运算作为对应3层的神经网络，可以将此式等效为y（x）=ax（其中a=c^3），没有隐藏层的神经网络

结论：

使用线性函数时，无法发挥多层网络带来的优势。因此，为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。

ReLU函数

ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输出0。
数学函数式如下：
（七式）

代码实现：

def relu(x):
 return np.maximum(0, x)
x=np.arange(-3,3,0.1)
y=relu(x)
plt.plot(x,y)
plt.ylim(-0.1,4)
plt.show

ReLU函数图形：

—————————————————————

2-3 多维数组的运算

使用Numpy多维数组的运算，实现高效率的神经网络。

创建一个多维数组

import numpy as np
A=np.array([1,2,3,4])
A,np.ndim(A),A.shape

[Out]: (array([1, 2, 3, 4]), 1, (4,))

B=np.array([[1,2],[3,4],[3,3]])
B.shape,B

[Out]: ((3, 2),
array([[1, 2],
[3, 4],
[3, 3]]))

矩阵的乘法 （涉及到线性代数的基础知识）

计算过程：

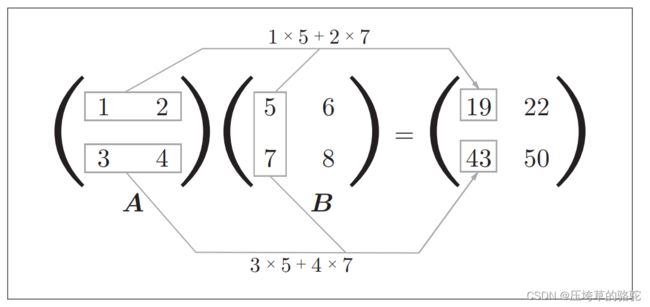
np.dot()接收两个NumPy数组作为参数，并返回数组的乘积。这里要注意的是，np.dot(A, B)和np.dot(B, A)的值可能不一样。 （与线性代数中的相同，必须满足矩阵的可乘性）
————————————————————————————————————————————

B=np.array([[1,2],[3,4],[3,3]])
C=np.eye(2,3)  #eye（）函数为生成单位矩阵
print(B.shape,C.shape)
np.dot(B,C)

【Out】

当不满足矩阵的乘法是（即：A矩阵的列数要等于B矩阵的行数），计算报错。

B=np.array([[1,2,3],[3,4,4],[3,3,3]])
C=np.eye(2,3)  #eye（）函数为生成单位矩阵
print(B.shape,C.shape)
np.dot(B,C)

B矩阵是 3行3列，C矩阵是2行3列，不满足矩阵的乘法规则。
————————————————————————————————————————————
下面来对比来看神经网络的内积问题

神经网络的内积

下面我们使用NumPy矩阵来实现神经网络。
以下举例了一个简单的神经网络。这个神经网络省略了偏置和激活函数，只有权重。

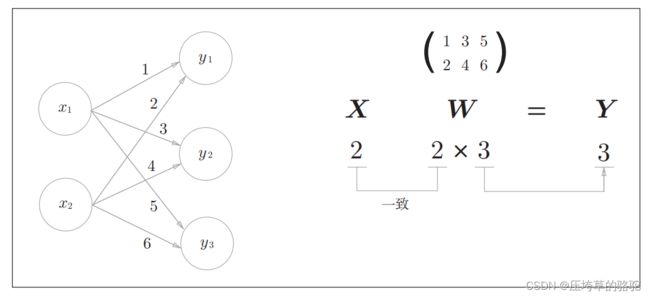
x=np.array([1,2])
w=np.array([[1,3,5],[2,4,6]])
y=np.dot(x,w)
y

【Out】：array([ 5, 11, 17])
————————————————————————————————————————————

2-4 三层神经网络的实现

巧妙地使用NumPy数组，可以用很少的代码完成神经网络的前向（从输入到输出这样一种方向称为前向）处理。

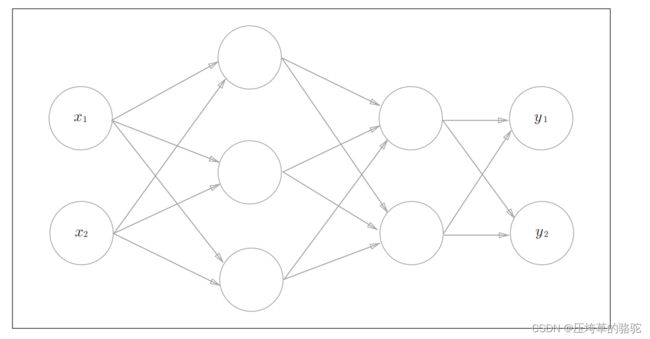
3层神经网络：输入层（第0层）有2个神经元，第1个隐藏层（第1层）有3个神经元，第2个隐藏层（第2层）有2个神经元，输出层（第3层）有2个神经元。

符号确认的概念：

本节的重点是神经网络的运算可以作为矩阵运算打包进行。因为神经网络各层的运算是通过矩阵的乘法运算打包进行的。
————————————————
怎么理解 权重符号：

各层间信号传递的实现

从输入层到第1层的第1个神经元的信号传递过程。

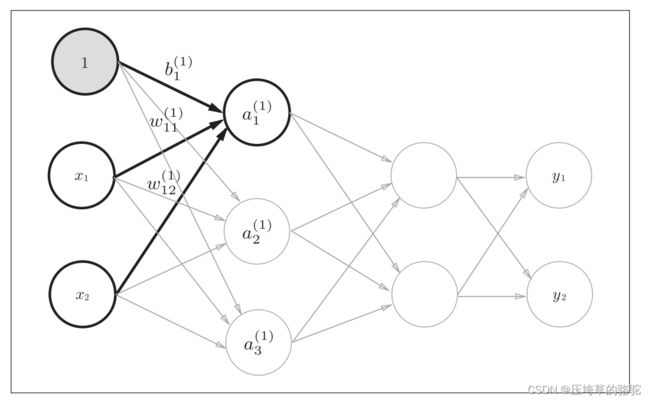
上图增加了表示偏置的神经元“1”。请注意，偏置的右下角的索引号只有一个。是因为前一层的偏置神经元（神经元“1”）只有一个。

注意

任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量（不包括后一层的偏置神经元“1”）
————————————————————————————————
通过加权信号和偏置的和按如下方式进行计算。

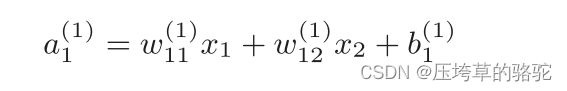
同时，我们运用矩阵的乘法运算，将第1层的加权和表示成数学式：

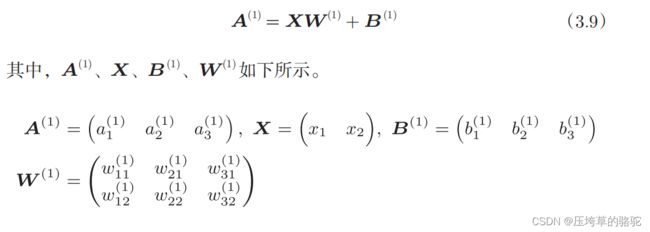
现在用python代码来实现这一个三层的神经网络：
——————————————————————————————

import numpy as np
X=np.array([1.0,0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
A1=np.dot(X,W1)+B1
Z1=sigmoid(A1)
Z1

从输入层到第1层的信号传递

接下来是从第一层到第二层的传递过程：

import numpy as np
X=np.array([1.0,0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
A1=np.dot(X,W1)+B1
Z1=sigmoid(A1) #Z1表示第一层的输入，第二层的输出
W2=np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

得到了第二层的输入去Z2。
——————————————————————————————
最后是第2层到输出层的信号传递，输出层的实现也和之前的实现基本相同。不过，最后的激活函数和之前的隐藏层有所不同。

def identity_function(x):
    return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)
print(Y)

这里我们定义了identity_function()函数（也称为“恒等函数”），并将其作为输出层的激活函数。恒等函数会将输入参数按原样输出，因此，这个例子中没有必要特意定义identity_function()。这里这样实现只是为了和之前的流程保持统一。另外，图3-20中，输出层的激活函数用σ()表示，不同于隐藏层的激活函数h()（σ读作sigma）。
（简单的说，为了保持一个固定的流程，定义了一个会输出参数本身的函数，并且最后一层的激活函数区别于之前的h()，用σ()）

从第2层到输出层的传递过程：

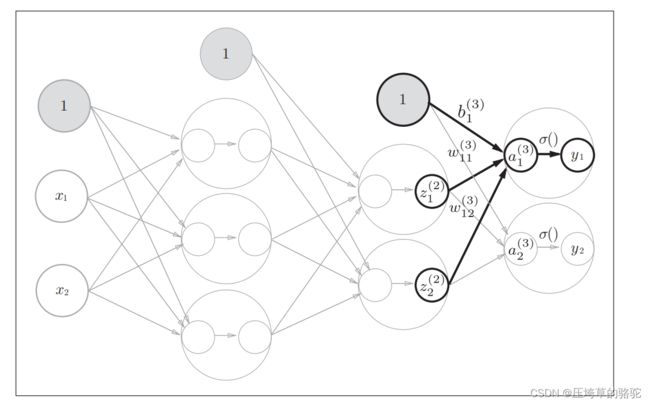
输出层所用的激活函数，要根据求解问题的性质决定。一般地，回归问题可以使用恒等函数，二元分类问题可以使用 sigmoid函数，多元分类问题可以使用 softmax函数。
——————————————————————————————
三层神经网络代码小结：
我们习惯把权重记为大写字母W1，其他的（偏置或中间结果等）都用小写字母表示。

#3层神经网络结构：
def init_network(): #初始化神经网络的各个参数，封装到network字典中
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network
def identity_function(x):#定义一个恒等函数
    return x
def sigmoid(x):
    return 1/(1+np.exp(-x))
def forward(network, x): #定义一个前向函数，用来表示输入信号转为换输出信号的处理过程
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)
    return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

2-5 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题softmax函数。
分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性的问题就是分类问题。
而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题。
——————————————————————————————

恒等函数和softmax函数

恒等函数：作为激活函数，会将输入的参数原封不动的输出，转换过程如图所示：

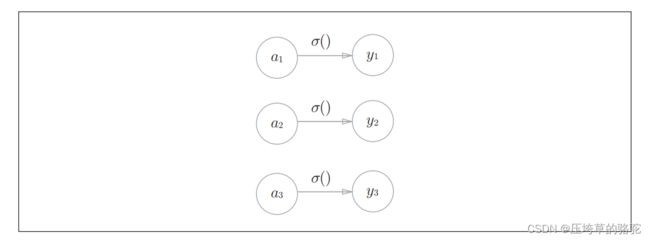
分类问题中使用的softmax函数：

假设输出层共有n个神经元，计算第k个神经元的输出Yk。(softmax函数的分子是输入信号ak的指数函数，分母是所有输入信号的指数
函数的和)

#定义一个softmax函数
def softmax(a):
    exp_a = np.exp(a) #分子
    sum_exp_a = np.sum(exp_a) # 分母
    y = exp_a / sum_exp_a
    return y

softmax函数的溢出问题
从数学式可以看出，e为底的指数函数，往往会导致数值过大，超过计算机的有效位数。
因此对上述数学式进行变形：

简单来说，分子分母同时乘以一个常数C，将C移入到指数函数中，记作Log C，将Log C 记作C’。
这里的C‘ 可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。
举例说明：

a=np.array([1000,1001,1002])
np.exp(a)/sum(np.exp(a))

【Out】：array([nan, nan, nan]) 没有被计算

a=np.array([1000,1001,1002])
c=np.max(a)
a-c
np.exp(a-c)/np.sum(np.exp(a-c))

【Out】:array([0.03511903, 0.25949646, 0.70538451])
对比：

a=np.array([5,6,7])
np.exp(a)/np.sum(np.exp(a))

【Out】：array([0.09003057, 0.24472847, 0.66524096])

a=np.array([1000,1002,1003])
c=np.max(a)
a-c
np.exp(a-c)/np.sum(np.exp(a-c))

【Out】：array([0.09003057, 0.24472847, 0.66524096])
说明了该数学推论的正确性。
因此在定义softmax函数时候，可以这样定义：

def softmax(x):
    c=np.max(x)
    exp_a=np.exp(a-c) #使用a-c
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return y

softmax 函数的特征：

它作为输出层的函数，它的输出值是0.0到1.0之间，并且softmax函数的输出值的总和是1.因此可以把softmax函数的输出解释为“概率”。
看例子：

a=np.array([0.2,0.3,0.4])
y=softmax(a)
print(y)
np.sum(y)

可以看到softmax的输出值的总和无限趋近于1（可以近似看作1），也就是说，从概率结果上来看，Y[0]的概率为30%，Y[1] 33%,Y[2]37%

输出层的神经元数量要多少个

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。比如，对于某个输入图像，预测是图中的数字0到9中的哪一个的问题（10类别分类问题），可以将神经元设定为10个。

参考：

《深度学习入门：基于Python的理论与实现 》斋藤康毅