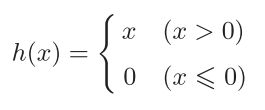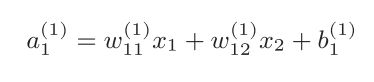深度学习入门基于python的理论与实现-神经网络

1 前言

在上一章感知机的学习中，我们知道感知机的异或门有可能表示任何复杂的函数，只要设置合适的权重即可，但是这是由人工来进行决定的----接下来神经网络可以解决这个问题。神经网络可以从数据学习到合适的权重参数。

2 神经网络是什么

2.1

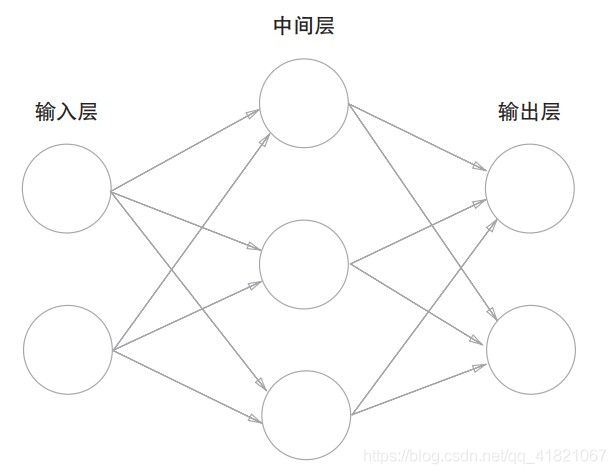
中间层又称为隐藏层，输入层，中间层，输出层分别是第0、1、2层。
如图，有三层神经元，但只有两层是有权重的。

2.2 激活函数

2.2.1 连接感知机和神经元的桥梁

多层感知机被称为神经网络。

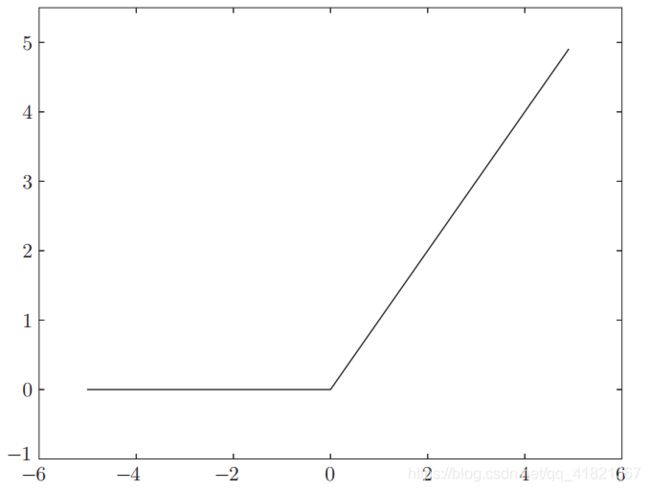
2.2.2 常用的激活函数

神经网络中使用的激活函数，sigmoid 函数


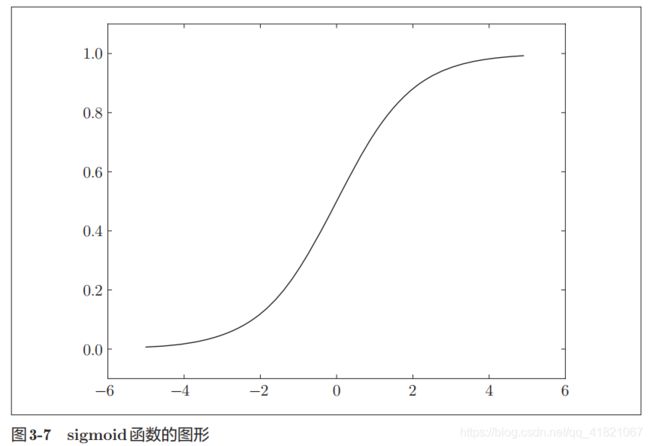
sigmoid 函数的曲线是平滑的，作为神经网络的激活函数的时候流动的是实数值信号。

Relu函数

2.3 线性函数和非线性函数

激活函数必须是非线性函数，才使得加深神经网络的层数才有意义，
线性函数无论如何加深神经网络，都不会出现隐藏层。

2.4 三层神经网络的实现

import numpy as np
x=np.array([1.0,0.5])
w1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
print(w1.shape)#2,3
print(B1.shape)#3
A1=np.dot(x,w1)+B1
print(A1)

然后再进行激活就OK啦。
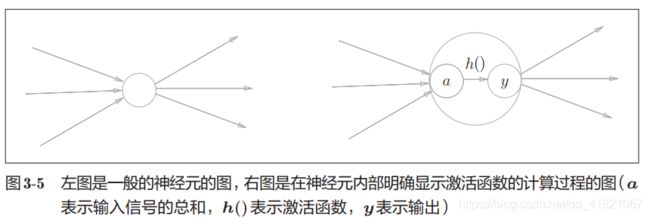
注意的是输出层的激活函数用sigma来表示，隐藏层的激活函数用h（）来表示

2.5 代码实现小结

import  numpy as np
def sigmoid(x):
    return 1/(1+np.exp(-x))
def init_network():
    network={}
    network['w1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
    network['b1']=np.array([0.1,0.2,0.3])
    network['w2']=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
    network['b2']=np.array([0.1,0.2])
    network['w3']=np.array([[0.1,0.3],[0.2,0.4]])
    network['b3']=np.array([0.1,0.2])
    return network

def forward(network,x):
    w1,w2,w3=network['w1'],network['w2'],network['w3']
    b1,b2,b3=network['b1'],network['b2'],network['b3']
    a1=np.dot(x,w1)+b1
    z1=sigmoid(a1)
    a2=np.dot(z1,w2)+b2
    z2=sigmoid(a2)
    a3=np.dot(z2,w3)+b3
    y=sigmoid(a3)
    return y

network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)

2.6 输出层的设计

神经网络用于回归问题和分类问题上，根据情况用不同的激活函数。
一般，回归用恒等函数，分类用softmax函数。
回归：根据图像预测一个人的体重
分类：区分图像中的是男还是女

这里来进行总结一下

1）恒等函数：就是直接原样输出，用在回归问题上
2）sigmoid函数：，用在二元分类问题上。
3）softmax函数：，用在多元分类问题上。
softmax 函数每个输出受所有输入的影响

import numpy as np
a = np.array([0.3,2.9,4.0])
exp_a=np.exp(a)
print(exp_a)
sum_exp_a=np.sum(exp_a)
print(sum_exp_a)
y=exp_a/sum_exp_a
print(y)

怎样解决softmax 函数的溢出问题？？

在下面的图中我们看到因为溢出计算机报错

每个输入信号减去输入信号的最大值

这时候就不会溢出了。。

softmax函数有哪些特征呢？
由上图可看到softmax函数输出的是0到1之间的数，并且输入数的和都为1，
这就是我们为什么把softmax 函数输出解释为概率

因为softmax函数是单调函数，所以输入信号到输出信号之间的大小关系不会改变。

在神经网络中，把输出的最大神经元所对应的类别，也就是输出值最大的那个叫为识别结果，所以在进行分类的时候，softmax 函数可以省略。以我们在实际上根本不需要softmax函数，直接看a元素就能知道哪个概率最大了（因为softmax需要指数运算，计算量挺大的）

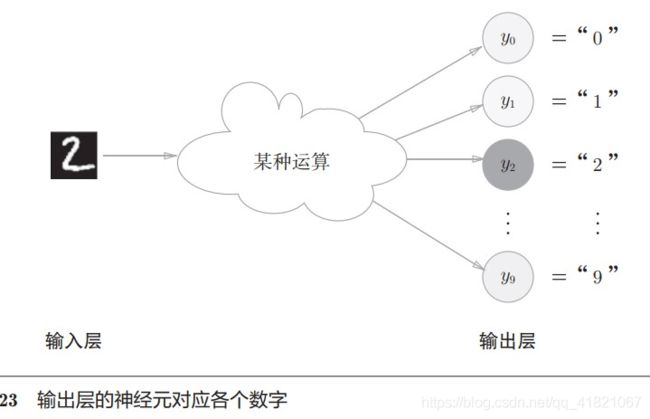
输出神经元数量由类别数量决定，如输出结果为0-9这10个类别，那么神经元输出则为10个。

3 手写数字识别

3.1 MNIST数据集

首先，mnist是机器学习最常用的数据集之一，

3.1.1 特点

1.0-9之间的数字构成
2.训练图像有6万张，测试图像有1万张，每张图片由28*28像素构成，各个像素的取值在0到255之间
由于我现在导入MNIST 包的时候出现问题，所以以后解决问题之后再练习代码