概率图模型--马尔可夫随机场
概率图模型–马尔可夫随机场 – 潘登同学的Machine Learning笔记
文章目录
- 概率图模型--马尔可夫随机场 -- 潘登同学的Machine Learning笔记
- 由贝叶斯网络过渡到马尔可夫链
-
- 简单回顾贝叶斯网络
- 由head-to-tail导出马尔可夫链
- 马尔可夫随机场(MRF)
-
- 马尔可夫随机场与马尔可夫链的关系
- 马尔可夫随机场
- 简单实例
- 加入节点势函数, 改进马尔可夫随机场
- 成对马尔可夫随机场
-
- 将图像处理问题转为定义在MRF上的最大后验概率推理问题
- 改写最大后验概率
- 总结
由贝叶斯网络过渡到马尔可夫链
简单回顾贝叶斯网络
![]()
贝叶斯网络有向无环图中的节点表示随机变量 { x 1 , x 1 , … , x n } \{x_1, x_1, \ldots, x_n\} {x1,x1,…,xn}(可以是可观测到的变量、隐变量、未知参数等); 认为有因果关系(非条件独立)就可以相连;
由head-to-tail导出马尔可夫链
- head-to-tail
上一篇文章强调了, head-to-tail是最重要一个结构, 现在将他推广成链式网络
根据head-to-tail的特征: 给定c的条件下b与a相互独立;
推广 给定 x i x_{i} xi的条件下, x i + 1 x_{i+1} xi+1的分布和 x 1 , x 2 , ⋯ , x i − 1 x_1,x_2,\cdots,x_{i-1} x1,x2,⋯,xi−1是相互独立的(通俗地说, 就是当前状态只与上一状态有关)
这样的链式网络就称为马尔科夫链
(马尔科夫链是一个很经典的模型, 后面的隐含马尔可夫模型、随机过程、NLP还得用上他)
马尔可夫随机场(MRF)
- 什么是马尔科夫随机场?
马尔可夫随机场(Markov Random Field)包含两层意思。
马尔可夫性质:它指的是一个随机变量序列按时间先后关系依次排开的时候,第N+1时刻的分布特性,与N时刻以前的随机变量的取值无关。拿天气来打个比方。如果我们假定天气是马尔可夫的,其意思就是我们假设今天的天气仅仅与昨天的天气存在概率上的关联,而与前天及前天以前的天气没有关系。其它如传染病和谣言的传播规律,就是马尔可夫的。
随机场:当给每一个位置中按照某种分布随机赋予相空间的一个值之后,其全体就叫做随机场。我们不妨拿种地来打个比方。其中有两个概念:位置(site),相空间(phase space)。“位置”好比是一亩亩农田;“相空间”好比是种的各种庄稼。我们可以给不同的地种上不同的庄稼,这就好比给随机场的每个“位置”,赋予相空间里不同的值。所以,俗气点说,随机场就是在哪块地里种什么庄稼的事情。
马尔可夫随机场:拿种地打比方,如果任何一块地里种的庄稼的种类仅仅与它邻近的地里种的庄稼的种类有关,与其它地方的庄稼的种类无关,那么这些地里种的庄稼的集合,就是一个马尔可夫随机场。
马尔可夫随机场与马尔可夫链的关系
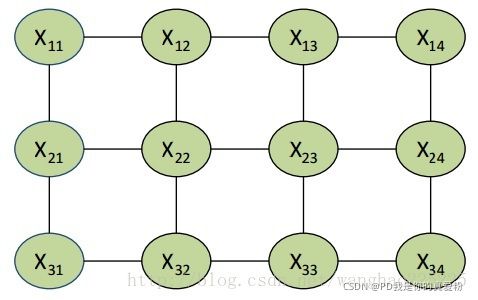
那不就是把很多条马尔可夫链合在一起, 然后从有向图变成无向图嘛?
但是最关键的东西不能丢, 就是当前状态只与周围的状态有关;
如: x 22 只 与 x 12 , x 21 , x 32 , x 23 x_{22} 只与 x_{12}, x_{21}, x_{32}, x_{23} x22只与x12,x21,x32,x23有关
马尔可夫随机场
-
是一个无向图概率模型
-
联合概率分布可以表示为:
P ( x 1 , x 2 , … , x n ) = 1 Z ϕ ∏ i = 1 k ϕ i ( D i ) P(x_1, x_2, \ldots, x_n) = \frac{1}{Z_{\phi}}\prod_{i=1}^{k}\phi_i(D_i) P(x1,x2,…,xn)=Zϕ1i=1∏kϕi(Di)
其中, Z ϕ Z_{\phi} Zϕ是联合概率分布的归一化因子, 通常称为分配函数, 其实只是为了保证所有情况加在一起的概率为1;
D i D_i Di是随机变量的集合, 因子 ϕ i ( D i ) \phi_i(D_i) ϕi(Di)是从随机变量集合导实数域的一个映射, 称为势函数或者因子; (说白了就是超参数)
- 马尔可夫随机场因子的集合
ϕ = { ϕ 1 ( D 1 ) , ϕ 2 ( D 2 ) , … , ϕ k ( D k ) } \phi = \{\phi_1(D_1), \phi_2(D_2), \ldots, \phi_k(D_k)\} ϕ={ϕ1(D1),ϕ2(D2),…,ϕk(Dk)}
- 某一个情形下的联合概率分布
P ~ ( x 1 , x 2 , … , x n ) = ∏ i = 1 k ϕ i ( D i ) \tilde{P}(x_1, x_2, \ldots, x_n) = \prod_{i=1}^{k}\phi_i(D_i) P~(x1,x2,…,xn)=i=1∏kϕi(Di)
- 归一化因子 (把所有情形加起来)
Z ϕ = ∑ x 1 , x 2 , … , x n P ~ ( x 1 , x 2 , … , x n ) Z_{\phi} = \sum_{x_1, x_2, \ldots, x_n}\tilde{P}(x_1, x_2, \ldots, x_n) Zϕ=x1,x2,…,xn∑P~(x1,x2,…,xn)
简单实例
- 这是一个简单的马尔可夫随机场
P ( A , B , C , D ) = 1 Z ϕ ∏ i = 1 k ϕ i ( D i ) = 1 Z ϕ ϕ 1 ( A , B ) ϕ 2 ( B , C ) ϕ 3 ( C , D ) ϕ 4 ( D , A ) \begin{aligned} P(A,B,C,D) &= \frac{1}{Z_{\phi}}\prod_{i=1}^{k}\phi_i(D_i) \\ &= \frac{1}{Z_{\phi}}\phi_1(A,B)\phi_2(B,C)\phi_3(C,D)\phi_4(D,A) \\ \end{aligned} P(A,B,C,D)=Zϕ1i=1∏kϕi(Di)=Zϕ1ϕ1(A,B)ϕ2(B,C)ϕ3(C,D)ϕ4(D,A)
- 势函数
| A | B | ϕ 1 ( A , B ) \phi_1(A,B) ϕ1(A,B) | B | C | ϕ 2 ( B , C ) \phi_2(B,C) ϕ2(B,C) | C | D | ϕ 3 ( C , D ) \phi_3(C,D) ϕ3(C,D) | D | A | ϕ 4 ( D , A ) \phi_4(D,A) ϕ4(D,A) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 30 | 0 | 0 | 100 | 0 | 0 | 1 | 0 | 0 | 100 |
| 0 | 1 | 5 | 0 | 1 | 1 | 0 | 1 | 100 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 100 | 1 | 0 | 1 |
| 1 | 1 | 10 | 1 | 1 | 100 | 1 | 1 | 1 | 1 | 1 | 100 |
势函数的值有概率含义, 值越大, 对应的概率就越大
然后对于某种情况, a = 0 , b = 0 , c = 0 , d = 1 a=0, b=0, c=0, d=1 a=0,b=0,c=0,d=1
势函数的连乘积:
30 × 100 × 100 × 1 = 300 , 000 30 \times 100 \times 100 \times 1 = 300,000 30×100×100×1=300,000
然后把所有情况, 即a,b,c,d的所有情况的势函数的连乘积的结果加起来, 做归一化, 求出归一化因子, 再用归一化因子与上面的300,000相乘就是 a = 0 , b = 0 , c = 0 , d = 1 a=0, b=0, c=0, d=1 a=0,b=0,c=0,d=1情况下的概率分布啦!
- 一个小问题: 局部势函数与边缘概率的关系?
P ( A , B ) = ∑ C , D P ( A , B , C , D ) P(A,B) = \sum_{C,D}P(A,B,C,D) P(A,B)=C,D∑P(A,B,C,D)
(接上例)
| A | B | P ( A , B ) P(A,B) P(A,B) | ϕ 1 ( A , B ) \phi_1(A,B) ϕ1(A,B) |
|---|---|---|---|
| 0 | 0 | 0.13 | 30 |
| 0 | 0 | 0.69 | 5 |
| 0 | 0 | 0.14 | 1 |
| 0 | 0 | 0.04 | 10 |
可以看出, 局部势函数与边缘概率没有之间的联系, 他们都是部分与整体的关系, 联合概率与边缘概率需要考虑所有变量间的概率依赖关系;
加入节点势函数, 改进马尔可夫随机场
(也不能说是改进, 只是有的场景需要节点势函数, 是为了让马尔可夫随机场更加泛用)
P ( A , B , C , D ) = 1 Z ϕ ϕ 1 ( A , B ) ϕ 2 ( B , C ) ϕ 3 ( C , D ) ϕ 4 ( D , A ) ϕ 5 ( A ) ϕ 6 ( B ) ϕ 7 ( C ) ϕ 8 ( D ) P(A,B,C,D) = \frac{1}{Z_{\phi}}\phi_1(A,B)\phi_2(B,C)\phi_3(C,D)\phi_4(D,A)\phi_5(A)\phi_6(B)\phi_7(C)\phi_8(D) P(A,B,C,D)=Zϕ1ϕ1(A,B)ϕ2(B,C)ϕ3(C,D)ϕ4(D,A)ϕ5(A)ϕ6(B)ϕ7(C)ϕ8(D)
成对马尔可夫随机场
(主要用于计算机视觉和图像处理领域)
P = 1 Z ϕ ∏ p ∈ V ϕ p ( x p ) ∏ ( p , q ) ∈ E ϕ p q ( x p , x q ) P = \frac{1}{Z_{\phi}}\prod_{p\in V}\phi_p(x_p)\prod_{(p,q)\in E}\phi_{pq}(x_p, x_q) P=Zϕ1p∈V∏ϕp(xp)(p,q)∈E∏ϕpq(xp,xq)
其中, V代表顶点集, E代表边集, 这都是图论最基础的表示方法;
前面的连乘就是节点势函数的连乘积, 后面的连乘就是边势函数的连乘积;
将图像处理问题转为定义在MRF上的最大后验概率推理问题
目标:
max x P ( x ) = ∏ p ∈ V ∏ p ∈ V ϕ p ( x p ) ∏ ( p , q ) ∈ E ϕ p q ( x p , x q ) \max_x P(x) = \prod_{p\in V}\prod_{p\in V}\phi_p(x_p)\prod_{(p,q)\in E}\phi_{pq}(x_p, x_q) xmaxP(x)=p∈V∏p∈V∏ϕp(xp)(p,q)∈E∏ϕpq(xp,xq)
注意: x p , x q x_p, x_q xp,xq表示的是在某一个情形中节点的取值, 对应回上面小例子的那个, 某一种情形指的就是 a = 0 , b = 0 , c = 0 , d = 1 a=0, b=0, c=0, d=1 a=0,b=0,c=0,d=1; 而 x p , x q x_p, x_q xp,xq理解为 a = 0 , b = 0 a=0, b=0 a=0,b=0(因为a,b相邻, 所以有边)
深刻理解: 成对马尔可夫随机场中参数与自变量
参数就是势函数: 不仅包括节点势函数, 也包括边的势函数;
自变量就是节点: 就是节点的某个取值;
-
举个栗子:
- A节点的势函数
A ϕ A \phi_{A} ϕA 0 5 1 1 - 自变量A
A 0 1
然后最大后验概率说白了, 就是把所有的可能答案带进去, 然后选最大的那个;
改写最大后验概率
(还是常规操作, log:变连乘为连加, 负号:求最大变求最小, 这一条操作如果你不会, 可以去康康pd的MLR推导)
- 取对数, 取负数
θ p ( x p ) = − log ϕ p ( x p ) θ p q ( x p , x q ) = − log ϕ p q ( x p , x q ) \theta_p(x_p) = - \log \phi_p(x_p) \\ \theta_pq(x_p, x_q) = - \log \phi_pq(x_p, x_q) \\ θp(xp)=−logϕp(xp)θpq(xp,xq)=−logϕpq(xp,xq)
- 等价于能量最小化问题(这个能量跟Loss函数一个意思)
min x E ( x ) = ∑ p ∈ V θ p ( x p ) + ∑ ( p , q ) ∈ E θ p q ( x p , x q ) \min_x E(x) = \sum_{p\in V}\theta_p(x_p) + \sum_{(p,q)\in E}\theta_pq(x_p, x_q) xminE(x)=p∈V∑θp(xp)+(p,q)∈E∑θpq(xp,xq)
总结
总的来说, 马尔可夫随机场与贝叶斯网络没有本质区别, 都是最大化后验概率, 关键还是在条件独立上, 理解了网络结构和势函数即可, 后面会有详细的算法实现;
马尔可夫随机场就是这样了, 继续下一章吧!pd的Machine Learning