机器学习-模型的评估与选择

• -

机器学习-模型的评估与选择

如今的世界AI出现的频率越来越高，相信过不了多久就会想java一样普及了。为了不使自己落后。只能跟上时代的步伐了，谁叫自己选择了一个对知识更新要求这么强的行业呢！

最近在看几本关于机器学习的数据。算法对于程序来说还是一如既往的是其根基。发现从周志华的《机器学习》入手理论更适合，写个博客分享一下。

《机器学习实战》和《统计学原理》可以同时看，会发现有些单看一本书不能理解的地方，看过三本书之后突然就悟了，当然还不能忘记同时在网上搜搜各种博客哈哈。

评价一个机器学习模型的好坏需要特定的评估方法，并据此对模型进行选择，从而得到一个更好的模型。

但在实际任务中，我们往往有很多的算法可供选择。甚至对同一个学习算法，使用不同的配置参数也会产生不同的模型。那么，我们该选用什么算法、什么配置？所以，本文主要介绍模型的选择与评估。

一：经验误差与过拟合

错误率 = a个样本分类错误/m个样本

精度 = 1 - 错误率 误差：学习器实际预测输出与样本的真是输出之间的差异。
训练误差：即经验误差。学习器在训练集上的误差。 泛化误差：学习器在新样本上的误差。

过拟合：学习器把训练样本学的”太好”，把不太一般的特性学到了，泛化能力下降，对新样本的判别能力差。必然存在，无法彻底避免，只能够减小过拟合风险。
欠拟合：对训练样本的一半性质尚未学好。

二：评估方法

1，留出法 2，交叉验证法 3，自助法 4，调参与最终模型

2.1留出法

D分为两个互斥的集合，一个作为S，一个作为T。

分层采样：S和T中正例和反例比例一样。

例如D包含500个正例，500反例。分层采样获得含70%样本的S，有350正例，350反例；30%样本的T，有150正例，150反例。数学定义上有：D=S∩T,S∪T=∅
一般采用随机划分、重复进行实验评估后取平均值作为留出法的评估结果。

例如，进行100次随机划分，每次产生一个训练/测试集用于实验评估，100次后得到100个结果，而留出法返回的则是这100个结果的平均。
弊端：T比较小，评估结果不够稳定准确，偏差大。
常见将大约2/3~4/5的样本用于训练，剩余样本用于测试。

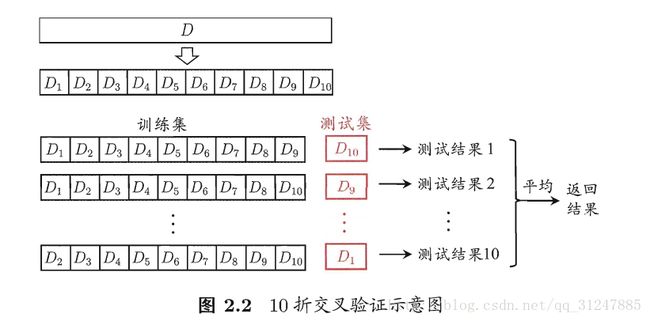
2.2，交叉验证法 将D划分为k个大小相似的互斥子集。(D通过分层采样得到每个子集Di,保持数据分布一致性)。每次用k-1个子集的并集作为训练集，余下那个作测试集。即可获得K组训练/测试集，进行K次训练和测试，最终返回k个测试结果的均值。也称”k折交叉验证”。数学定义上有：D=D1∪D2∪⋯∪Dk,Di∩Dj=∅(i≠j)

为减小因样本划分不同而引入的差别，k折交叉验证要随机使用不同的划分重复p次，最终评估结果是这p次k折交叉验证结果的均值，即进行p*k次训练/测试。

留一法：m个样本划分成m个子集，每个子集包含一个样本。留一法中被实际评估的模型与期望评估的用D训练出来的模型很相似，因此，留一法的评估结果往往被认为比较准确。
留一法缺陷：数据集较大，例如，数据集包含100w个样本，则需训练100w个模型。且留一法的估计结果未必比其他评估法准确。

2.3，自助法

以自助采样法（bootstrapsampling）为基础，从m个样本的数据集D，随机采样(选)一个样本，拷贝入训练D’，放回，继续随机挑选，直至m次。

样本在m次采样中始终不被踩到的概率(1-1/m)^m。

实际评估的模型与期望评估的模型都使用m个训练样本，而仍有约1/3的没有在训练集的样本用于测试。
自助法在数据集较小、难以有效划分训练/测试集时很有用。在初始数据量足够时，留出法和交叉验证法更常用。

2.4，调参与最终模型

对每种参数都训练处结果模型，然后选出最好的学习模型。这种想法是正确的，但需要注意，学习算法很多是在实数范围内取值，因此对每种参数都训练出模型来是不可行的。现实中常用的做法是：对每个参数选定一个变化步长，如在[0,0.2]范围以内已0.05为步长。则实际要评估的候选参数值有5个，最终从这5个中选出定值。显然，这样选定的参数值往往不是“最佳”值，但这是在计算机开销和性能估计之间折中的的结果。通过这个折中机器学习才变的可行，事实上，通过这样的折中调参任然很困难。例如：假定有3个参数，每个参数有5个候选值，这样对每组训练/训练集就有3^5=125个模型需要考察。像大型的“深度学习”的参数往往有上百亿个。
在给定的m个样本的数据集D，在模型的选择中往往会留出一部分数据做为训练模型。因此应该在模型选用完成之后，学习算法和配置参数已选定，再使用D数据集重新训练模型，这个模型的训练过程中使用了m个样本，这才是我们最后交给用户的模型。

三：性能度量

性能度量：衡量模型泛化能力的评价标准。

给定样例集D={(x1,y1),(x2,y2),……,(xm,ym)},yi是对xi的真实标记，要评估学习器f的性能，就要把学习器预测结果f(x)与真实标记y进行比较。
均方误差：

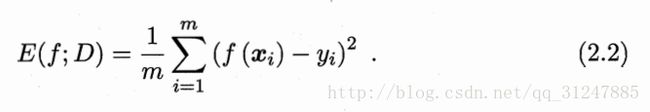
　　数据分布D和概率密度函数p(.),均方误差：
　　
　　1，错误率与精度 2，查准率和查全率 3，ROC AUC 4，代价敏感错误率与代价曲线

3.1，错误率与精度 错误率：分类错误的样本数占样本总数的比例。
精度：分类正确的样本数占样本总数的比例。

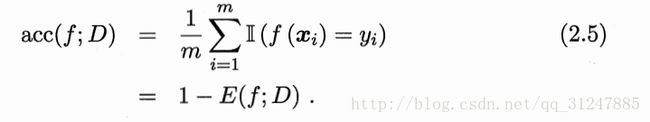
数据分布D和概率密度函数p(.)。

错误率：

精度：

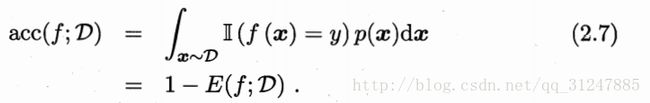
3.2，查准率和查全率 对于二分类的问题可分为：
True positive 真正例，False positive 假正例，True negative 真反例，False negative 假反例，TP+FP+TN+FN = 样例总数，如图：

查准率P和查全率R分别定义为：

通常，查准率高时，查全率偏低；查全率高时，查准率偏低。
例如，若希望好商品尽可能的挑选出来，则可通过增加选商品的数量来实现，查准率就会低；若希望挑出的商品中好商品比例尽可能高，则可挑选有把握的商品，必然会漏掉好商品，查全率就低了。
学习器把最可能是正例的样本排在前面。按此排序，把样本作为正例进行预测，根据PR绘图。
“平衡点”是：查准率=查全率，在一些应用中对查全率和查准率的要求是不同的，如：商品推荐更希望推荐的内容是用户感兴趣的，则查准率更为看重。公安系统的检索当中则更看重查全率。